直観主義論理
直観主義論理(ちょっかんしゅぎろんり、英: intuitionistic logic)または直観論理(ちょっかんろんり)、あるいは構成的論理(こうせいてきろんり、英: constructive logic)とは、ある種の論理体系であり、伝統的な真理値の概念が構成的証明の概念に置き換わっている点で古典論理とは異なる。例えば古典論理では、全ての論理式に真か偽の真理値 ( ) が割り当てられる。このときその真理値に対する直接的なエビデンスを持つか否かは問題にしない。これはどのような曖昧な命題においても「真か偽かが決定可能である」ということを意味する。対照的に、直観主義論理では確定的に論理式に真理値を割り当てるのではなく、それが真であるとは「直接的なエビデンス」つまり「証明」があることと見做す。
証明論的な視点から見ると、直観主義論理は古典論理の制限であって排中律や二重否定除去が公理として許容されないものである。排中律や二重否定除去はいくつかの論理式に対しては個別に証明できることがあるけれども、古典論理のように普遍的に成立することはない。
直観主義論理の色々な意味論が研究されている。ひとつの意味論は古典的なブール代数値意味論を写しとったものでブール代数の代わりにハイティング代数を用いる。別の意味論ではクリプキ・モデルを用いる。
直観主義論理は実際的な有用性を持つ。何故ならばこの制限によって存在具体性を持つ証明が作られるからであり、これは直観主義論理が数学的構成主義のある形態として適当なものとする。非正式には、ある対象が存在することの構成的証明があれば、その構成的証明はそのような対象の例を生成するアルゴリズムとして使える、ということを意味する。
形式化された直観主義論理はアレン・ハイティングによってヤン・ブラウワーの直観主義プログラムの形式的な基礎として発展せられたものである。
構文論と証明体系[編集]
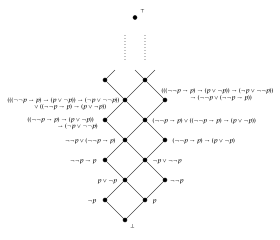
直観主義論理の論理式の構文は古典命題論理や古典述語論理と類似である。しかしながら、直観主義的な論理結合子は、古典論理におけるように、他の論理結合子を用いて定義することはできない。(そのため , , などの論理結合子だけを用いて定式化することはできない。)直観主義命題論理では習慣的に を基本的な結合子として採用する。ここで は の省略形として扱う。直観主義述語論理ではこれに量化記号 を加える。
多くの古典論理の恒真式は直観主義的には証明できない。排中律 だけでなくパースの法則 や二重否定除去 などがその例である。古典論理において二重否定導入 と二重否定除去 はともに定理である。直観主義論理においては前者のみが定理である。すなわち二重否定を導入することはできるが、除去することはできない。ただし三重否定除去 は定理である。排中律 の拒絶は古典論理に親しい者には奇妙に思われるが、直観主義論理で命題論理式を証明するには、全ての可能な命題論理式に対して真または偽の証明が要求され、これは様々な理由によって不可能である。
多くの古典論理で妥当な恒真式は直観主義論理では定理でないが、全ての直観主義論理で妥当な定理は古典論理に於いても妥当であるから、直観主義論理は古典論理を弱めたものであるという見方ができる。ただし直観主義論理は古典論理にはない良い性質を多く持っている。
シークエント計算[編集]
ゲンツェンは彼の体系LK(古典論理のシークエント計算)の簡単な制限として直観主義論理の健全かつ完全な体系が得られることを見つけた。彼はこの体系をLJと呼んだ。LKにおいて任意個の論理式がシークエントの結論(右側)に来ることを許すが、LJにおいては高々ひとつの論理式だけを許す。この結果として例えば含意右の適用において直観主義的に許容できない推論が禁じられることから、直観主義論理の体系が得られるのである。(右辺が複数であることを許すと含意右を用いて α→α,⊥ から →α,¬α が得られ、排中律が導かれる。右辺を制限した結果として含意右が制限されて直観主義論理の体系が得られる。)
LKを制限して得られる直観主義論理の体系で結論が複数であることを許容するものもある。LJ'[1]はその例である。
ヒルベルト流の計算[編集]
直観主義論理は次のようにヒルベルト流の計算を用いても定義できる。これは古典命題論理の公理化(Propositional calculus#Alternative calculus)に類似である。
命題論理では、推論規則としてモーダスポネンス
- MP: および から を導く
を取り、公理図式として次のものを取る:
- THEN-1:
- THEN-2:
- AND-1:
- AND-2:
- AND-3:
- OR-1:
- OR-2:
- OR-3:
- FALSE:
一階述語論理の体系を作るには次の推論規則を加える:
- -GEN: から を導く;ただし固有変数条件「 は に自由に現れない」を満たす
- -GEN: から を導く;ただし固有変数条件「 は に自由に現れない」を満たす
また次のものを公理図式に加える:
- PRED-1: ただし項 t は の中の x への代入について自由である (つまり t の中の変数記号は の中で束縛されていない)
- PRED-2: ただしPRED-1と同様の条件を満たす
オプションの結合子[編集]
否定[編集]
もし否定を表す結合子 を なる省略形の代わりに導入したいならば、次を公理に加えれば十分である:
- NOT-1':
- NOT-2':
否定を導入した代わりに偽を表す命題定数 を落としたいならば次のようにする。まず FALSE, NOT-1', NOT-2' を次の公理に置き換える:
- NOT-1:
- NOT-2:
NOT-1の代替としては または などがある。
同値[編集]
同値を表す結合子 は standing for の省略形として導入できる。代わりに次の公理を追加してもよい:
- IFF-1:
- IFF-2:
- IFF-3:
IFF-1とIFF-2は一つの公理 に結合できる。
古典論理との関係[編集]
古典論理の体系は次のどれかを公理に追加することによって得られる:
- (排中律。これは とも定式化できる。)
- (二重否定除去)
- (パースの法則)
一般に、古典論理の恒真式で二元クリプキ・フレーム で妥当でない公理を追加したもの(言い換えればSmetanich論理に含まれないもの)を考えれば、これは古典論理に等しい。Smetanich論理は古典論理よりも弱く直観主義論理より強い論理の中で極大なものだからである。
別の関係性としてはゲーデル=ゲンツェン変換によるものがある。これは古典一階述語論理が直観主義一階述語論理に埋め込めることを示す。すなわち一階述語論理式が古典論理で証明可能であることと、それをゲーデル・ゲンツェン変換したものが直観主義論理で証明可能であることとが同値となる。またグリベンコの定理によれば、命題論理式が古典論理で証明可能であることと、それを二重否定したものが直観主義論理で証明可能であることとは同値である。したがって直観主義論理は古典論理を構成的意味論の観点から拡大したものと見做すことができる。
1932年にクルト・ゲーデルは古典論理と直観主義論理の間にあるゲーデル論理の体系を定義した。これは中間論理として知られる。
結合子の定義不可能性[編集]
古典命題論理において、論理積、論理和または実質含意を基本的なものとすれば、他は否定を用いてウカシェヴィッチの命題論理のようにして定義できる。またこれら4つをパースの矢印(NOR)やシェファーの棒(NAND)のようなただひとつの論理結合子を用いて定義することもできる。同様に、古典一階述語論理において、一方の量化子は他方と否定を用いて定義できる。
これらは全ての結合子はブール関数であるという二値原理からの基本的な帰結である。二値原理は直観主義論理においては成り立たない。ただ無矛盾律だけが成り立つ。結果として、いかなる結合子も不要ではなく、上に述べたどの公理も必要であることが分かる。古典論理において成立する同値性は、直観主義論理においては、幾つかは成り立つけれども、多くは一方の含意だけが成り立つ。次のようなものがある:
論理積と論理和:
論理積と含意:
論理和と含意:
全称量化と存在量化:
すると、例えば、 "a or b" は "if not a, then b" よりも強い主張となる。これは古典論理において同値であることと対照的である。他方で "not (a or b)" と "not a, and also not b" は同値となる。
同値を結合子のリストに入れるならば、いくつかの結合子は他から定義できる:
とりわけ と は直観主義的結合子の完全な基底となる。
意味論[編集]
直観主義論理の意味論は古典論理のそれよりも複雑である。直観主義論理のモデル論はハイティング代数やクリプキ意味論として与えられている。最近ではタルスキ流のモデル論の完全性がBob Constableによって証明せられた。ただしこの完全性は通常の意味のそれとは異なる。
ハイティング代数意味論[編集]
古典論理において、我々はしばしば論理式の取る真理値について議論する。この値は普通はブール代数の元から選ぶ。ブール代数の交わりと結びは論理結合子の と に同一視される。そして の真理値は と の真理値のブール代数における交わりとする。このとき論理式が古典論理において妥当であることと、任意のブール代数とその上で値を取る真理値割り当てに対して論理式の真理値が であることとが同値となる。
直観主義論理においても同様の完全性定理が成立するが、論理式の真理値はブール代数の代わりにハイティング代数の元を用いる。ブール代数はハイティング代数の特別な場合である。このとき論理式が直観主義論理で妥当であることと、任意のハイティング代数とその上で値を取る真理値割り当てに対して論理式の真理値が であることは同値である。
論理式が妥当であることを確かめる為には、ひとつのハイティング代数の上で調べれば十分であることが証明できる。そのハイティング代数は数直線 の開部分集合からなるハイティング代数である。[2] この代数系において、 と は集合の交わりと結びである。また は すなわち の補集合と との和集合の内部である。(これは古典論理における含意の演算の結果を開集合になるように調整したものである。様相論理の観点から見るとこれは必然性を外側に付けているのと同じことになる。) は空集合 であり、 は全体集合 である。否定 は と定義されるが、これは の補集合の開核すなわち外部と一致する。この対応付けによって直観主義的に妥当な論理式はちょうど空間全体が割り当てられるものと一致する。[2]
例えば矛盾律 は妥当である。なぜなら開集合 を の付値としてどのように選んでも の値は次のように直線全体となるからである:
位相空間論によれば は の部分集合であり、 との共通部分は空であるから、
したがってこの論理式の付値は真であり、妥当であることが従う。
しかし排中律 は非妥当である。それには に を割り当てるとよい。すると の付値は の内部、すなわち であり、目的の論理式の付値は および の和集合、すなわち となる。これは空間全体に一致しない。
数直線からハイティング代数を作る上のやり方は任意の位相空間に対しても適用できる。位相空間論では閉包の開核がもとと一致する集合を正則開集合という。これはこのハイティング代数における二重否定で不変な集合と同じものである。正則開集合の全体は(完備)ブール代数を成す。これは古典論理が二重否定によって直観主義論理に埋め込めるというグリベンコの定理に対応している。
クリプキ意味論[編集]
タルスキ流のモデル論[編集]
他の論理との関係[編集]
直観主義論理の双対[注 1]は双対直観論理(英: dual-intuitionistic logic)である[3]。双対直観論理は矛盾許容論理の一種であり、ブラジリアン論理(英: Brazilian logic)、反直観主義論理(英: anti-intuitionistic logic)などと呼ばれる論理と対応している[4]。
直観主義論理から爆発原理の公理を取り除いたものは最小論理として知られる。
多値論理との関係[編集]
クルト・ゲーデルは1932年に直観主義論理が多値論理ではないことを証明した。(#ハイティング代数意味論は直観主義論理の"無限多値論理"としての解釈の一種と見られる。)
中間論理との関係[編集]
任意の有限ハイティング代数でブール代数でないものは(意味論的に)中間論理を定める。他方で、純粋な直観主義論理における論理式の妥当性は、特定のハイティング代数に結びついたものではなく、あらゆるハイティング代数に関係している。
様相論理との関係[編集]
直観主義命題論理の論理式は次のように様相命題論理S4の論理式に翻訳できる:
| = | ||
| = | ||
| = | ||
| = | ||
| = | ||
| = |
またこれにより直観主義論理を模倣できる[5]。すなわち翻訳された論理式が様相命題論理S4で妥当であることと、翻訳前の論理式が直観主義命題論理IPCで妥当であることは同値である。上のような変換はゲーデル=マッキンゼー=タルスキ変換と呼ばれる。
様相論理S4の直観主義版は構成的様相論理CS4と呼ばれる[6]。
ラムダ計算[編集]
カリー=ハワード対応はIPCと直和と直積を持つ単純型付きラムダ計算との間に拡張できる。[6]
関連項目[編集]
脚注[編集]
注釈[編集]
- ^ ここでの双対はシークエント計算においての双対である。
出典[編集]
- ^ Proof Theory by G. Takeuti, ISBN 0-444-10492-5
- ^ a b Sørensen, Morten Heine B; Paweł Urzyczyn (2006). Lectures on the Curry-Howard Isomorphism. Studies in Logic and the Foundations of Mathematics. Elsevier. p. 42. ISBN 0-444-52077-5
- ^ Urbas, Igor (1996-07-01). “Dual-Intuitionistic Logic”. Notre Dame Journal of Formal Logic 37 (3). doi:10.1305/ndjfl/1039886520. ISSN 0029-4527.
- ^ Aoyama, Hiroshi (2004). “LK, LJ, Dual Intuitionistic Logic, and Quantum Logic”. Notre Dame Journal of Formal Logic 45 (4): 193–213. doi:10.1305/ndjfl/1099238445.
- ^ Lévy, Michel (2011年4月29日). “Logique modale propositionnelle S4 et logique intuitioniste propositionnelle” (PDF). pp. 4–5. 2015年5月8日閲覧。
- ^ a b Natasha Alechina, Michael Mendler, Valeria de Paiva, and Eike Ritter. “Categorical and Kripke Semantics for Constructive S4 Modal Logic” (PDF). 2015年5月8日閲覧。
参考文献[編集]
- 前原昭二『数学基礎論』財団法人放送大学教育振興会
- van Dalen, Dirk, 2001, "Intuitionistic Logic", in Goble, Lou, ed., The Blackwell Guide to Philosophical Logic. Blackwell.
- Morten H. Sørensen, Paweł Urzyczyn, 2006, Lectures on the Curry-Howard Isomorphism (chapter 2: "Intuitionistic Logic"). Studies in Logic and the Foundations of Mathematics vol. 149, Elsevier.
- W. A. Carnielli (with A. B.M. Brunner)."Anti-intuitionism and paraconsistency". Journal of Applied Logic Volume 3, Issue 1, March 2005, pages 161-184.
外部リンク[編集]
- Stanford Encyclopedia of Philosophy: "Intuitionistic Logic"—by Joan Moschovakis.
- Intuitionistic Logic by Nick Bezhanishvili and Dick de Jongh (from the Institute for Logic, Language and Computation at the University of Amsterdam)
- Semantical Analysis of Intuitionistic Logic I by Saul A. Kripke from Harvard University, Cambridge, Mass., USA
- Intuitionistic Logic by Dirk van Dalen
- The discovery of E.W. Beth's semantics for intuitionistic logic by A.S. Troelstra and P. van Ulsen
- Expressing Database Queries with Intuitionistic Logic (FTP one-click download) by Anthony J. Bonner. L. Thorne McCarty. Kumar Vadaparty. Rutgers University, Department of Computer Science.
- Tableaux'method for intuitionistic logic through S4-translation tests the intuitionistic validity of propositional formulae; provided by the Laboratoire d'Informatique de Grenoble.
- Validity tester for IPC (based on Mezhirov's game for IPC) at playmycode.com































































































![{\displaystyle (-\infty ,0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0241c015ef4c611c9c9aeafb395e7c4a16178405)













