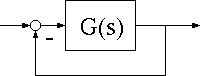古典制御論
古典制御論(こてんせいぎょろん、英語:classical control theory)は、伝達関数と呼ばれる線形の入出力システムとして表された制御対象を中心に、周波数応答などを評価して望みの挙動を達成する制御理論である。1950年代に体系化された。代表的な成果物と言えるPID制御は、その扱い易さから現在でも産業では主力である。
主な概念[編集]
モデル表現[編集]
- 伝達関数 (transfer function)
- 系の入力と出力のラプラス変換の比を取ったもの。 などと表す。複素数の有理多項式で表現される。 を純虚数 に置き換えることで、周波数 に対する特性を調べることができる。
- (例)
解析手法[編集]
- 根(root)または零点 (zero)、極 (pole)
- 一般に多項式が零となるような方程式の解を根または零点と呼ぶ。古典制御論では、伝達関数の分子多項式の零点を指す。次に述べる特性多項式の零点を極と呼ぶ。
- (例)
- の零点は 、極は となる。この場合、極の実部がともに負であるから、安定である。
- 特性多項式 (characteristic polynomial)、特性方程式 (characteristic equation)
- 伝達関数の分母多項式で、入出力応答を支配する。これを零とする方程式を特性方程式と呼び、その解を極と呼ぶ。極の実部の符号により安定性や収束性が、虚部によって振動特性などが判別できる。
- (例)
- の特性多項式は
- ラウス・フルビッツの安定判別法 (Routh–Hurwitz stability criterion)
- 特性方程式を解かずに、特性多項式の係数のみから安定性を判別する方法
- 閉ループ系 (closed loop system)
- 出力を引き戻し入力側で足し合わせて接続した系。足し合わせる際に、そのまま足したものを正帰還(positive feedback)、符号を変えて引いたものを負帰還(negative feedback)と呼ぶ。フィードバックも参照。
- 一巡伝達関数 (loop transfer function)
- 閉ループ系を構成する際、入力部分での接続を切り放したときの、入力から引き戻した部分までの伝達関数
- (例) 下図のような負帰還の閉ループ系の場合、一巡伝達関数は となる。
- ベクトル軌跡 (vector locus)
- 信号の周波数を変化させたときの伝達関数 の複素数としての軌跡を複素平面に描いたもの
- ナイキスト (Nyquist) の安定判別法
- 一巡伝達関数のベクトル軌跡をナイキスト軌跡と呼び、その形状などから安定性を判別する方法
- 根軌跡法 (root locus method)
- 閉ループゲインを変化させたときの閉ループ伝達関数の極(特性方程式の根)の軌跡を複素平面に描いたもの(根軌跡)によって安定性や挙動を調べる方法
- ボード線図 (bode diagram、bode plot)
- 横軸に周波数(角周波数)、縦軸に伝達関数のゲイン と位相遅れ を片対数グラフとして描いたもの。周波数領域での特性を評価するのに用いられる。
- ニコルス線図 (Nichols chart)
制御系設計[編集]
- PID制御 (PID control)
- 出力信号の比例(proportional)成分、積分(integral)成分、微分(derivative)成分を入力にフィードバックさせる制御。比例ゲイン 、積分ゲイン 、微分ゲイン を適当に定めてやるというシンプルながら効果的な制御方法である。現在でも産業界では主流であると言われる。ゲインの調整法にはステップ応答法、限界感度法などがある。