「フォック状態」の版間の差分
初版はおそらくen:Fock state 03:34, 26 December 2016 UTCからの翻訳 |
en:Fock state (03:34, 26 December 2016 )の残りを翻訳 タグ: サイズの大幅な増減 |
||
| 5行目: | 5行目: | ||
粒子表現は、[[ポール・ディラック]]が[[ボース粒子]]について、[[パスクアル・ヨルダン]]と[[ユージン・ウィグナー]]が[[フェルミ粒子]]について詳細に扱ったのが最初である。<ref name="Friedrichs">{{Cite Book| last = Friedrichs| first = K. O.| title = Mathematical aspects of the Quantum Theory of Fields| publisher = Interscience Publishers| date = 1953| asin = B0006ATGK4 }}</ref>{{rp|35}} |
粒子表現は、[[ポール・ディラック]]が[[ボース粒子]]について、[[パスクアル・ヨルダン]]と[[ユージン・ウィグナー]]が[[フェルミ粒子]]について詳細に扱ったのが最初である。<ref name="Friedrichs">{{Cite Book| last = Friedrichs| first = K. O.| title = Mathematical aspects of the Quantum Theory of Fields| publisher = Interscience Publishers| date = 1953| asin = B0006ATGK4 }}</ref>{{rp|35}} |
||
==定義== |
|||
N個の相互作用の無い同種粒子の多粒子状態を、N個の1粒子状態の[[テンソル積]]の和として規定する。 |
|||
テンソル積は、粒子がフェルミ粒子かボース粒子かによって、下部(underlying)1粒子[[ヒルベルト空間]]の交代積または対称積でなければならない。 |
|||
粒子数が変化する場合は、それぞれの粒子数におけるテンソル積ヒルベルト空間の直和として[[フォック空間]]を構成する。 |
|||
このとき各1粒子状態における粒子数を規定することで、同じ状態を占有数表示で規定することができる。 |
|||
'''k'''<sub>i</sub>を下部1粒子ヒルベルト空間における状態の正規直交基底とする。 |
|||
この基底から、フォック空間での基底である「占有数基底」が導かれる。 |
|||
フォック空間における状態が占有数基底の要素であるとき、その状態を'''フォック状態'''と呼ばれる。 |
|||
フォック状態は次の重要な基準を満足する。 |
|||
つまりそれぞれの''i''における状態は、[[粒子数演算子]]<math>\widehat{N_{{\mathbf{k}}_i}}</math>の固有状態で、基となった''i''番目の状態'''k'''<sub>i</sub>に対応する。 |
|||
この固有状態に対応する固有値は、その状態における粒子数を与える。 |
|||
この基準はフォック状態をほとんど定義している(厳密にはさらに位相因子を選択しなければならない)。 |
|||
得られたフォック状態は、次のように表す。 |
|||
:<math>|n_{{\mathbf{k}}_1},n_{{\mathbf{k}}_2},..n_{{\mathbf{k}}_i}...\rangle</math> |
|||
この表現における<math>n_{{\mathbf{k}}_i}</math>とは、i番目の状態'''k'''<sub>i</sub>における粒子数である。 |
|||
i番目の状態における粒子数演算子<math>\widehat{N_{{\mathbf{k}}_i}}</math>は、フォック状態に以下のように作用する。 |
|||
:<math>\widehat{N_{{\mathbf{k}}_i}}|n_{{\mathbf{k}}_1},n_{{\mathbf{k}}_2},..n_{{\mathbf{k}}_i}...\rangle=n_{{\mathbf{k}}_i}|n_{{\mathbf{k}}_1},n_{{\mathbf{k}}_2},..n_{{\mathbf{k}}_i}...\rangle</math> |
|||
よってフォック状態は、固有値<math>n_{{\mathbf{k}}_i}</math>を持つ数演算子の固有状態である |
|||
<ref name="Mandel">{{Cite book| last = Mandel| first = Wolf| title = Optical coherence and quantum optics| publisher = Cambridge University Press| date = 1995| isbn = 0521417112 }}</ref>{{rp|478}}。 |
|||
フォック状態は、フォック空間の最も便利な[[基底 (線型代数学)|基底]]を作る。 |
|||
フォック空間の要素の中で、[[粒子数]]が異なる状態の重ね合わせであるものは、数演算子の固有状態ではないためフォック状態ではない。 |
|||
よってフォック空間の全ての要素が「フォック状態」と呼ばれる訳ではない。 |
|||
フォック状態の定義より<math>{\rm Var}(\widehat{N})=0</math>、すなわちフォック状態における粒子数の測定は、常にゆらぎが無く確定値を与える。 |
|||
よって、 |
|||
:<math>\widehat{N}=\sum_i \widehat{N_{{\mathbf{k}}_i}}</math> |
|||
==2粒子での例== |
|||
任意の終状態<math>|f\rangle</math>、2つの同種粒子のフォック状態<math>|1_{{\mathbf{{k}}_1}}, 1_{{\mathbf{{k}}_2}}\rangle</math>、[[演算子 (物理学)|演算子]]<math> \widehat{\mathbb{O}} </math>について、 |
|||
次の[[同種粒子|不可弁別性]]条件が成り立つ。 |
|||
<ref name=FGross>{{Cite book|last= Gross|first= Franz|title= Relativistic Quantum Mechanics and Field Theory|publisher= Wiley-VCH|date= 1999|isbn= 0471353868}}</ref>{{rp|191}} |
|||
:<math>|\langle f|\widehat{\mathbb{O}}|1_{{\mathbf{{k}}_1}}, 1_{{\mathbf{{k}}_2}}\rangle|^2=|\langle f|\widehat{\mathbb{O}}|1_{{\mathbf{{k}}_2}}, 1_{{\mathbf{{k}}_1}}\rangle|^2</math>. |
|||
よって<math>\langle f|\widehat{\mathbb{O}}|1_{{\mathbf{{k}}_1}}, 1_{{\mathbf{{k}}_2}}\rangle=e^{i\delta}\langle f|\widehat{\mathbb{O}}|1_{{\mathbf{{k}}_2}}, 1_{{\mathbf{{k}}_1}}\rangle</math>で、 [[ボース粒子]]のときは<math>e^{i\delta}=+1</math>、[[フェルミ粒子]]のときは<math>-1</math>である。 |
|||
<math>\langle f| </math>と<math>\widehat{\mathbb{O}}</math>は任意であるため、 |
|||
ボース粒子では<math>|1_{{\mathbf{{k}}_1}}, 1_{{\mathbf{{k}}_2}}\rangle=+|1_{{\mathbf{{k}}_2}}, 1_{{\mathbf{{k}}_1}}\rangle</math>、 |
|||
フェルミ粒子では<math>|1_{{\mathbf{{k}}_1}}, 1_{{\mathbf{{k}}_2}}\rangle=-|1_{{\mathbf{{k}}_2}}, 1_{{\mathbf{{k}}_1}}\rangle</math>である |
|||
<ref name=FGross/>{{rp|191}}。 |
|||
ここで数演算子ではボース粒子とフェルミ粒子を区別せず、対称性を考慮せずに粒子を数えるだけであることに注意。。 |
|||
この2種類の粒子の差を見るには、生成消滅演算子と呼ばれる別の演算子が必要となる。 |
|||
==ボース粒子フォック状態== |
|||
[[ボース粒子]]は整数スピンを持つ粒子で「合成した固有状態は[[交換演算子]]が作用したとき対称的である」という単純なルールに従う<ref name="TIFR">{{Cite web| url=http://theory.tifr.res.in/~sgupta/courses/qm2013/hand13.pdf| title= Quantum Mechanics 1 Lecture Notes on Identical Particles, TIFR, Mumbai}}</ref>。 |
|||
たとえばテンソル積表現での2粒子系においては次のようになる。 |
|||
:<math>\hat{P}\left|x_1, x_2\right\rangle = \left|x_2, x_1\right\rangle</math>。 |
|||
===ボース粒子の生成消滅演算子=== |
|||
この新しいフォック空間表現では、同じ対称性の性質を表現することができるはずである。 |
|||
そのためボース粒子の非エルミートな[[生成消滅演算子]]を導入し、それぞれ<math>b^{\dagger}</math>、<math>b</math>と表す。 |
|||
これらの演算子のフォック状態への作用は次の2つの式で与えられる。 |
|||
:<math>b^{\dagger}_{{\mathbf{k}}_l}|n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,n_{{\mathbf{k}}_{3}}...n_{{\mathbf{k}}_{l}},...\rangle=\sqrt{n_{{\mathbf{k}}_{l}} +1 } |n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,n_{{\mathbf{k}}_{3}}...n_{{\mathbf{k}}_{l}}+1 ,...\rangle </math> <ref name="TIFR"/> |
|||
:<math>b_{{\mathbf{k}}_l}|n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,n_{{\mathbf{k}}_{3}}...n_{{\mathbf{k}}_{l}},...\rangle=\sqrt{n_{{\mathbf{k}}_{l}}} |n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,n_{{\mathbf{k}}_{3}}...n_{{\mathbf{k}}_{l}}-1 ,...\rangle </math> <ref name="TIFR"/> |
|||
[[File:Action of operator on bosonic fock state.jpg|center|''ボース粒子フォック状態への生成消滅演算子の作用'']] |
|||
====生成消滅演算子のエルミート性==== |
|||
生成消滅演算子はエルミート演算子ではない<ref name="TIFR"/>。 |
|||
:{| class="toccolours collapsible collapsed" width="60%" style="text-align:left" |
|||
!生成消滅演算子がエルミート演算子ではない証明 |
|||
|- |
|||
| フォック状態<math> |n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,n_{{\mathbf{k}}_{3}}...n_{{\mathbf{k}}_{l}},...\rangle</math>において、 |
|||
:<math>\langle n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,n_{{\mathbf{k}}_{3}}...n_{{\mathbf{k}}_{l}}-1,...|b_{{\mathbf{k}}_l}|n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,n_{{\mathbf{k}}_{3}}...n_{{\mathbf{k}}_{l}},...\rangle = \sqrt{n_{{\mathbf{k}}_{l}}}\langle n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,n_{{\mathbf{k}}_{3}}...n_{{\mathbf{k}}_{l}}-1,...|n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,n_{{\mathbf{k}}_{3}}...n_{{\mathbf{k}}_{l}}-1,...\rangle </math> |
|||
:<math>(\langle n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,n_{{\mathbf{k}}_{3}}...n_{{\mathbf{k}}_{l}},...|b_{{\mathbf{k}}_l}|n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,n_{{\mathbf{k}}_{3}}...n_{{\mathbf{k}}_{l}}-1,...\rangle)^* </math> |
|||
:<math>= \langle n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,n_{{\mathbf{k}}_{3}}...n_{{\mathbf{k}}_{l}}-1...|b_{{\mathbf{k}}_l}^{\dagger}|n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,n_{{\mathbf{k}}_{3}}...n_{{\mathbf{k}}_{l}},...\rangle=\sqrt{n_{{\mathbf{k}}_{l}}+1}\langle n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,n_{{\mathbf{k}}_{3}}...n_{{\mathbf{k}}_{l}}-1...|n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,n_{{\mathbf{k}}_{3}}...n_{{\mathbf{k}}_{l}}+1...\rangle </math> |
|||
よって生成(消滅)演算子のエルミート共役は、自分自身にはならない。よってエルミート演算子ではない。 |
|||
しかし生成(消滅)演算子のエルミート共役は、消滅(生成)演算子である<ref name="Altland">{{Cite book |
|||
| last = Altland, Alexander |
|||
| first = Simons, Ben |
|||
| title = Condensed Matter Field Theory |
|||
| publisher = Cambridge University Press |
|||
| date = 2006 |
|||
| url = https://books.google.com/books?id=0KMkfAMe3JkC&pg=PA39#v=onepage&q&f=false |
|||
| isbn = 0521769752}}</ref>。{{rp|45}} |
|||
|} |
|||
====演算子の交換関係==== |
|||
[[ボース粒子]]系での生成消滅演算子の交換関係は、 |
|||
: <math>[b^{\,}_i, b^\dagger_j] \equiv b^{\,}_i b^\dagger_j - b^\dagger_jb^{\,}_i = \delta_{i j},</math> <ref name="TIFR"/> |
|||
: <math>[b^\dagger_i, b^\dagger_j] = [b^{\,}_i, b^{\,}_j] = 0,</math> <ref name="TIFR"/> |
|||
ここで<math>[\ \ , \ \ ]</math>は[[交換子]]、<math>\delta_{i j}</math>は[[クロネッカーのデルタ]]である。 |
|||
===Nボース粒子基底状態<math>|n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,n_{{\mathbf{k}}_{3}}...n_{{\mathbf{k}}_{l}},...\rangle</math> === |
|||
{| class="wikitable" |
|||
|- |
|||
! 粒子数 (N) !! ボース粒子基底状態<ref name="Bruus">{{Cite book| last = Bruus| first = Flensberg| title = Many-Body Quantum Theory in Condensed Matter Physics: An Introduction | publisher = OUP Oxford| date = 2003| isbn = 0198566336 }}</ref>{{rp|11}} |
|||
|- |
|||
| 0 || <math>|0,0,0...\rangle</math> |
|||
|- |
|||
| 1 || <math>|1,0,0...\rangle</math>,<math>|0,1,0...\rangle</math>,<math>|0,0,1...\rangle</math>,... |
|||
|- |
|||
| 2 || <math>|2,0,0...\rangle</math>,<math>|1,1,0...\rangle</math>,<math>|0,2,0...\rangle</math>,... |
|||
|- |
|||
| ... || ... |
|||
|- |
|||
|} |
|||
===具体的なフォック状態への作用=== |
|||
* 真空状態(どの状態にも粒子が無い状態)<math> |0_{{\mathbf{k}}_{1}}, 0_{{\mathbf{k}}_{2}} ,0_{{\mathbf{k}}_{3}}...0_{{\mathbf{k}}_{l}},...\rangle</math>では、 |
|||
::<math>b^{\dagger}_{{\mathbf{k}}_l}|0_{{\mathbf{k}}_{1}}, 0_{{\mathbf{k}}_{2}} ,0_{{\mathbf{k}}_{3}}...0_{{\mathbf{k}}_{l}},...\rangle=|0_{{\mathbf{k}}_{1}}, 0_{{\mathbf{k}}_{2}} ,0_{{\mathbf{k}}_{3}}...1_{{\mathbf{k}}_{l}} ,...\rangle </math> |
|||
::<math>b_{{\mathbf{k}}_l}|0_{{\mathbf{k}}_{1}}, 0_{{\mathbf{k}}_{2}} ,0_{{\mathbf{k}}_{3}}...0_{{\mathbf{k}}_{l}},...\rangle=0 </math> <ref name="TIFR"/> |
|||
* '''生成演算子'''を真空状態に作用させることで、どんなフォック状態も作ることができる。 |
|||
::<math> |n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ...\rangle=\frac{(b^{\dagger}_{{\mathbf{k}}_1})^{{\mathbf{k}}_1}}{\sqrt{{{\mathbf{k}}_1}!}} \frac{(b^{\dagger}_{{\mathbf{k}}_2})^{{\mathbf{k}}_2}}{\sqrt{{{\mathbf{k}}_2}!}}...|0_{{\mathbf{k}}_{1}}, 0_{{\mathbf{k}}_{2}} ,...\rangle</math> |
|||
* <math> |n_{{\mathbf{k}}}\rangle</math>と表される単一モードフォック状態では、 |
|||
::<math>b^{\dagger}_{\mathbf{k}}|n_{{\mathbf{k}}}\rangle=\sqrt{n_{\mathbf{k}} +1} |n_{{\mathbf{k}}}+1\rangle </math> |
|||
::<math>b_{\mathbf{k}}|n_{{\mathbf{k}}}\rangle=\sqrt{n_{\mathbf{k}}} |n_{{\mathbf{k}}}-1\rangle </math> |
|||
===数演算子の作用=== |
|||
ボース粒子系での数演算子は、次のように与えられる。 |
|||
:<math>\widehat{N_{{\mathbf{k}}_l}}=b^{\dagger}_{{\mathbf{k}}_l}b_{{\mathbf{k}}_l}</math> |
|||
これがボース粒子フォック状態に作用すると、次のようになる。 |
|||
:<math>\widehat{N_{{\mathbf{k}}_l}}|n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,n_{{\mathbf{k}}_{3}}...n_{{\mathbf{k}}_{l}}...\rangle=n_{{\mathbf{k}}_{l}} |n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,n_{{\mathbf{k}}_{3}}...n_{{\mathbf{k}}_{l}}...\rangle </math> <ref name="TIFR"/> |
|||
また数演算子はエルミート演算子である。 |
|||
===ボース粒子フォック状態の対称的ふるまい=== |
|||
生成消滅演算子の交換関係により、ボース粒子フォック状態が粒子交換において対称的なふるまいを示す。 |
|||
ここで2つの状態間の粒子の交換は、ある状態でのある粒子を消滅させ、別の状態での粒子を生成させることで行われる。 |
|||
フォック状態<math>|n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,....n_{{\mathbf{k}}_{m}}...n_{{\mathbf{k}}_{l}}...\rangle</math> |
|||
から出発して状態<math>k_l</math>から状態<math>k_m</math>への粒子をシフトさせたい場合は、交換関係より<math>b_{{\mathbf{k}}_{m}}^{\dagger}.b_{{\mathbf{k}}_{l}}=b_{{\mathbf{k}}_{l}}.b_{{\mathbf{k}}_{m}}^{\dagger}</math>であるため、 |
|||
:<math>b_{{\mathbf{k}}_{m}}^{\dagger}.b_{{\mathbf{k}}_{l}}|n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,....n_{{\mathbf{k}}_{m}}...n_{{\mathbf{k}}_{l}}...\rangle=b_{{\mathbf{k}}_{l}}.b_{{\mathbf{k}}_{m}}^{\dagger}|n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,....n_{{\mathbf{k}}_{m}}...n_{{\mathbf{k}}_{l}}...\rangle=\sqrt{n_{{\mathbf{k}}_{m}} +1 }\sqrt{n_{{\mathbf{k}}_{l}}}|n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,....n_{{\mathbf{k}}_{m}}+1...n_{{\mathbf{k}}_{l}}-1...\rangle</math> |
|||
よってボース粒子フォック空間は交換演算子の作用において対称的である。 |
|||
==フェルミ粒子フォック空間== |
|||
===フェルミ粒子の生成消滅演算子=== |
|||
[[フェルミ粒子]]の反対称的なふるまいを保持するために、フェルミ粒子の非エルミートな[[生成消滅演算子]]を導入する。 |
|||
フェルミ粒子フォック状態 <math> |n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,n_{{\mathbf{k}}_{3}}...n_{{\mathbf{k}}_{l}},...\rangle</math>に'''生成演算子'''を次のように作用させる。 |
|||
:<math>c^{\dagger}_{{\mathbf{k}}_l}|n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,n_{{\mathbf{k}}_{3}}...n_{{\mathbf{k}}_{l}},...\rangle=\sqrt{n_{{\mathbf{k}}_{l}} +1 } |n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,n_{{\mathbf{k}}_{3}}...n_{{\mathbf{k}}_{l}}+1 ,...\rangle </math> <ref name="TIFR"/> |
|||
'''消滅演算子'''は次のように作用する。 |
|||
:<math>c_{{\mathbf{k}}_l}|n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,n_{{\mathbf{k}}_{3}}...n_{{\mathbf{k}}_{l}},...\rangle=\sqrt{n_{{\mathbf{k}}_{l}}} |n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,n_{{\mathbf{k}}_{3}}...n_{{\mathbf{k}}_{l}}-1 ,...\rangle </math> <ref name="TIFR"/> |
|||
これら2つの演算子の作用は反対称的に行われる(後述)。 |
|||
====演算子の交換関係==== |
|||
[[フェルミ粒子]]系における生成消滅演算子の反交換関係は、 |
|||
: <math>\{c^{\,}_i, c^\dagger_j\} \equiv c^{\,}_i c^\dagger_j + c^\dagger_jc^{\,}_i = \delta_{i j},</math> <ref name="TIFR"/> |
|||
: <math>\{c^\dagger_i, c^\dagger_j\} = \{c^{\,}_i, c^{\,}_j\} = 0,</math> <ref name="TIFR"/> |
|||
ここで<math>{\{ \ , \ \} }</math> は[[反交換子]]、<math>\delta_{i j}</math>は[[クロネッカーのデルタ]]である。これらの反交換関係は、フェルミ粒子フォック状態の反対称的なふるまいを表すために用いられる。 |
|||
===数演算子の作用=== |
|||
[[フェルミ粒子]]の数演算子は次のように与えられる。 |
|||
:<math>\widehat{N_{{\mathbf{k}}_l}}=c^{\dagger}_{{\mathbf{k}}_l}.c_{{\mathbf{k}}_l}</math> |
|||
これがフェルミ粒子フォック状態に作用すると、 |
|||
:<math>\widehat{N_{{\mathbf{k}}_l}}|n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,n_{{\mathbf{k}}_{3}}...n_{{\mathbf{k}}_{l}}...\rangle=n_{{\mathbf{k}}_{l}} |n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,n_{{\mathbf{k}}_{3}}...n_{{\mathbf{k}}_{l}}...\rangle </math> <ref name="TIFR"/> |
|||
====最大占有数==== |
|||
生成消滅演算子や数演算子の作用はボース粒子の場合と同じであるように見えるが、フェルミ粒子フォック状態の最大占有数から違いが生じる。 |
|||
上述の2つのフェルミ粒子の例を拡張し、 |
|||
次のように置換演算子のある特定の和を固有ケットのテンソル積に適用することで、 |
|||
フェルミ粒子フォック状態<math>|n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,n_{{\mathbf{k}}_{3}}...n_{{\mathbf{k}}_{l}}...\rangle</math>が得られることをまず確かめておかなければならない。 |
|||
:<math>|n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,n_{{\mathbf{k}}_{3}}...n_{{\mathbf{k}}_{l}}...\rangle=S_{-}|i_{1}, i_{2},i_{3}...i_{l}...\rangle=\frac{1}{\sqrt{N!}}\begin{vmatrix} |
|||
|i_{1}\rangle_{1} & \cdots & |i_{1}\rangle_{N} \\ |
|||
\vdots & \ddots & \vdots \\ |
|||
|i_{N}\rangle_{1} & \cdots & |i_{N}\rangle_{N} |
|||
\end{vmatrix}</math> <ref name="Schwabl">{{Cite book |
|||
| last = Schwabl, Hilton, Lahee |
|||
| title = Advanced Quantum Mechanics |
|||
| publisher = Springer |
|||
| date = 2008 |
|||
| isbn = 3540850619 }}</ref>{{rp|16}} |
|||
この行列式は[[スレーター行列式]]と呼ばれる{{cn|reason=What does the determinant entry i_1)_N mean?|date=April 2015}}。 |
|||
もしいかなる1粒子状態も同じであればスレーター行列式の2つの行は同じであり、よって行列式は0になる。 |
|||
よって2つの同種[[フェルミ粒子]]は同じ状態を占めるはずがない。 |
|||
よっていかなる単一状態の占有数も0または1のどちらかである。 |
|||
フェルミ粒子フォック状態に関連する固有値<math>\widehat{N_{{\mathbf{k}}_l}}</math>は0または1である。 |
|||
===Nフェルミ粒子基底状態 <math>|n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,n_{{\mathbf{k}}_{3}}...n_{{\mathbf{k}}_{l}},...\rangle</math> === |
|||
{| class="wikitable" |
|||
|- |
|||
! 粒子数 (N) !! フェルミ粒子基底状態<ref name="Bruus"/>{{rp|11}} |
|||
|- |
|||
| 0 || <math>|0,0,0...\rangle</math> |
|||
|- |
|||
| 1 || <math>|1,0,0...\rangle</math>,<math>|0,1,0...\rangle</math>,<math>|0,0,1...\rangle</math>,... |
|||
|- |
|||
| 2 || <math>|1,1,0...\rangle</math>,<math>|0,1,1...\rangle</math>,<math>|0,1,0,1...\rangle</math>,<math>|1,0,1,0...\rangle</math>... |
|||
|- |
|||
| ... || ... |
|||
|- |
|||
|} |
|||
===具体的なフォック状態への作用=== |
|||
[[File:Action of operators on fermionic fock state.jpg|center|フェルミ粒子フォック状態への生成消滅演算子の作用。]] |
|||
* <math> |0_{{\mathbf{k}}}\rangle</math>で表される単一モードフェルミ粒子フォック状態では、 |
|||
::<math>c^{\dagger}_{\mathbf{k}}|0_{{\mathbf{k}}}\rangle=|1_{{\mathbf{k}}}\rangle </math> |
|||
::<math>c^{\dagger}_{\mathbf{k}}|1_{{\mathbf{k}}}\rangle=0 </math> |
|||
:つまりいかなる状態でも最大占有数は1で、1個以上のフェルミ粒子は同じ状態を占有できない。 |
|||
* <math> |1_{{\mathbf{k}}}\rangle</math>で表される単一モードフェルミ粒子フォック状態において、 |
|||
::<math>c_{\mathbf{k}}|1_{{\mathbf{k}}}\rangle=|0_{{\mathbf{k}}}\rangle </math> |
|||
::<math>c_{\mathbf{k}}|0_{{\mathbf{k}}}\rangle=0 </math> |
|||
:つまり粒子数は0以下になれない。 |
|||
* <math>|n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}},... n_{{\mathbf{k}}_{\beta}},n_{{\mathbf{k}}_{\alpha}},...\rangle</math>で表される多重モードフェルミ粒子フォック状態では、 |
|||
::<math>c_{{\mathbf{k}}_{\alpha}}|n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}},... n_{{\mathbf{k}}_{\beta}},n_{{\mathbf{k}}_{\alpha}},...\rangle= (-1)^{\sum_{\beta < \alpha} n_\beta} |n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}},... n_{{\mathbf{k}}_{\beta}},1-n_{{\mathbf{k}}_{\alpha}},...\rangle</math> |
|||
ここで<math>(-1)^{\sum_{\beta < \alpha} n_\beta}</math>は、[[ヨルダン-ウィグナー変換|ヨルダン-ウィグナーストリング]]と呼ばれ、含まれる1粒子状態の順序に依存し、全ての前に来る状態のフェルミ粒子占有数を足し合わせる。<ref name= "Altland"/>{{rp|88}} |
|||
===フェルミ粒子フォック状態の反対称的なふるまい=== |
|||
交換演算子のもとでのフェルミ粒子状態の反対称的な振る舞いは、反交換関係によるものである。 |
|||
ここでは2つの状態間の粒子の交換は、ある状態のある粒子を消滅させ、別の粒子を生成させることで行われる。 |
|||
フォック状態<math>|n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,....n_{{\mathbf{k}}_{m}}...n_{{\mathbf{k}}_{l}}...\rangle</math>から出発して状態<math>k_l</math>から状態 <math>k_m</math>へ粒子をシフトさせたい場合、反交換関係より<math>c_{{\mathbf{k}}_{m}}^{\dagger}.c_{{\mathbf{k}}_{l}}=-c_{{\mathbf{k}}_{l}}.c_{{\mathbf{k}}_{m}}^{\dagger}</math>であるため、 |
|||
:<math>c_{{\mathbf{k}}_{m}}^{\dagger}.c_{{\mathbf{k}}_{l}}|n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,....n_{{\mathbf{k}}_{m}}...n_{{\mathbf{k}}_{l}}...\rangle=\sqrt{n_{{\mathbf{k}}_{m}} +1 }\sqrt{n_{{\mathbf{k}}_{l}}}|n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,....n_{{\mathbf{k}}_{m}}+1...n_{{\mathbf{k}}_{l}}-1...\rangle</math> |
|||
しかし、 |
|||
:<math>c_{{\mathbf{k}}_{l}}.c_{{\mathbf{k}}_{m}}^{\dagger}|n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,....n_{{\mathbf{k}}_{m}}...n_{{\mathbf{k}}_{l}}...\rangle=-c_{{\mathbf{k}}_{m}}^{\dagger}.c_{{\mathbf{k}}_{l}}|n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,....n_{{\mathbf{k}}_{m}}...n_{{\mathbf{k}}_{l}}...\rangle=-\sqrt{n_{{\mathbf{k}}_{m}} +1 }\sqrt{n_{{\mathbf{k}}_{l}}}|n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,....n_{{\mathbf{k}}_{m}}+1...n_{{\mathbf{k}}_{l}}-1...\rangle</math> |
|||
よってフェルミ粒子フォック状態は、交換演算子の作用のもとでは反対称的にふるまう。 |
|||
==フォック状態は一般的にエネルギー固有状態では無い== |
|||
[[第二量子化]]理論では、[[ハミルトニアン密度]]関数は次のように与えられる。 |
|||
:<math>\mathfrak{H}=\frac {1}{2m} \nabla_{i}\psi^{*}(x)\nabla_{i}\psi(x)</math> <ref name="FGross"/>{{rp|189}} |
|||
全[[ハミルトニアン]]は、次のように与えられる。 |
|||
:<math>\mathcal{H}=\int d^{3}x\,\mathfrak{H}=\int d^{3}x \psi^{*}(x)\left(-\tfrac{\nabla^2}{2m}\right)\psi(x) \quad (\therefore \mathfrak{H}=-\tfrac{\nabla^2}{2m})</math> |
|||
自由粒子のシュレーディンガー方程式<ref name="FGross"/>{{rp|189}} は、 |
|||
:<math>\mathfrak{H}\psi_{n}^{(+)}(x)=-\tfrac{\nabla^2}{2m}\psi_{n}^{(+)}(x)=E_{n}^{0}\psi_{n}^{(+)}(x)</math> |
|||
この解は直交性を満たす。 |
|||
:<math>\int d^{3}x\, \psi_{n}^{(+)^{*}}(x)\psi_{n'}^{(+)}(x)=\delta_{nn'}</math> |
|||
また消滅演算子を<math>a_n</math>として、次の関係がある。 |
|||
:<math>\psi(x)=\sum_n a_n \psi_{n}^{(+)}(x)</math> |
|||
よって、 |
|||
:<math>\therefore \mathcal{H}=\sum_{n,n'}\int d^{3}x\, a^{\dagger}_{n'}\psi_{n'}^{(+)^{*}}(x)\mathfrak{H}a_n \psi_{n}^{(+)}(x)</math> |
|||
相互作用しない粒子においてのみ、<math>\mathfrak{H}</math>と<math>a_n</math>が交換する。しかし一般の場合にはこれらは交換しない。 |
|||
相互作用しない粒子では、 |
|||
:<math>\mathcal{H}=\sum_{n,n'}\int d^{3}x\, a^{\dagger}_{n'}\psi_{n'}^{(+)^{*}}(x)E^{0}_{n}\psi_{n}^{(+)}(x)a_n |
|||
=\sum_{n,n'}E^{0}_{n}a^{\dagger}_{n'}a_n\delta_{nn'}=\sum_{n}E^{0}_{n}a^{\dagger}_{n}a_n=\sum_{n}E^{0}_{n}\widehat{N}</math> |
|||
これらが交換しない場合、ハミルトニアンは上述の表現を持たない。 |
|||
よって一般的にフォック状態は系のエネルギー固有状態ではない。 |
|||
==真空ゆらぎ== |
|||
真空状態または<math>|0\rangle</math>は最低エネルギーの状態で、<math>a</math>と<math>a^{\dagger}</math>の期待値はこの状態では0になる。 |
|||
:<math>a|0\rangle = 0 = \langle0|a^{\dagger}</math> |
|||
電磁場とベクトルポテンシャルは同じ一般形のモード展開を持つ。 |
|||
:<math>F(\vec{r},t) = \varepsilon a e^{i\vec{k}x-\omega t} + h\cdot c </math> |
|||
これらの場の演算子の期待値が真空状態では0になることを見るのは簡単である。 |
|||
:<math>\langle0|F|0\rangle = 0 </math> |
|||
しかし、これらの場の演算子の二乗の期待値は0ではないことを示すことができる。 |
|||
このように0アンサンブル平均についての場におけるゆらぎが存在する。 |
|||
これらの真空ゆらぎは、量子光学における[[ラムシフト]]など多くの興味深い現象の原因となる。 |
|||
==多重モードフォック状態== |
|||
多重モード場におけるそれぞれの生成消滅演算子は、それ自身のモードに作用する。 |
|||
たとえば<math>a_{{\mathbf{k}}_{l}}</math>と<math>a^{\dagger}_{{\mathbf{k}}_{l}}</math>は、<math>|n_{{\mathbf{k}}_{l}}\rangle</math>にだけ作用する。 |
|||
異なるモードに対応する演算子はヒルベルト空間の異なる部分空間に作用するため、全体の場は全てのモードにわたる<math>|n_{{\mathbf{k}}_l}\rangle </math> の直積である。 |
|||
:<math>|n_{{\mathbf{k}}_{1}}\rangle |n_{{\mathbf{k}}_{2}}\rangle |n_{{\mathbf{k}}_{3}}\rangle... \equiv |n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,n_{{\mathbf{k}}_{3}}...n_{{\mathbf{k}}_{l}}...\rangle \equiv |\{n_{\mathbf{k}}\}\rangle </math> |
|||
生成消滅演算子の多重モード状態への作用は、それら自身のモードの数状態を上昇または下降させるだけである。 |
|||
:<math> a_{{\mathbf{k}}_l} |n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,n_{{\mathbf{k}}_{3}}...n_{{\mathbf{k}}_{l}},...\rangle = \sqrt{n_{{\mathbf{k}}_{l}}} |n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,n_{{\mathbf{k}}_{3}}...n_{{\mathbf{k}}_{l}}-1 ,...\rangle </math> |
|||
:<math> a^{\dagger}_{{\mathbf{k}}_l} |n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,n_{{\mathbf{k}}_{3}}...n_{{\mathbf{k}}_{l}},...\rangle = \sqrt{n_{{\mathbf{k}}_{l}} +1 } |n_{{\mathbf{k}}_{1}}, n_{{\mathbf{k}}_{2}} ,n_{{\mathbf{k}}_{3}}...n_{{\mathbf{k}}_{l}}+1 ,...\rangle </math> |
|||
ここで各モードの数演算子の和である、場の全[[数演算子]]を定義する。 |
|||
:<math> \hat{n}_{\mathbf{k}} = \sum \hat{n}_{\mathbf{k}_l} </math> |
|||
多重モードフォック状態は全数演算子の固有ベクトルであり、固有値は全てのモードの全占有数である。 |
|||
:<math> \hat{n}_{\mathbf{k}} |\{n_{\mathbf{k}}\}\rangle = \bigg( \sum n_{\mathbf{k}_l} \bigg) |\{n_{\mathbf{k}}\}\rangle </math> |
|||
相互作用しない粒子では、数演算子とハミルトニアンは互いに交換し、よって多重モードフォック状態は多重モードハミルトニアンの固有状態になる。 |
|||
:<math> \hat{H} |\{n_{\mathbf{k}}\}\rangle = \bigg( \sum \hbar \omega \big(n_{\mathbf{k}_l} + \frac{1}{2} \big)\bigg) |\{n_{\mathbf{k}}\}\rangle </math> |
|||
==単一フォトン状態の源== |
|||
単一フォトンは、シングルエミッター(原子、[[窒素-空孔中心]]<ref>C. Kurtsiefer, S. Mayer, P. Zarda, Patrick and H. Weinfurter, (2000), "Stable Solid-State Source of Single Photons", ''Phys. Rev. Lett.'' '''85''' (2) 290--293, [http://link.aps.org/doi/10.1103/PhysRevLett.85.290 doi 10.1103/PhysRevLett.85.290]</ref>、 [[量子ドット]]<ref>C. Santori, M. Pelton, G. Solomon, Y. Dale and Y. Yamamoto (2001), "Triggered Single Photons from a Quantum Dot", ''Phys. Rev. Lett.'' '''86''' (8):1502--1505 [http://link.aps.org/doi/10.1103/PhysRevLett.86.1502 DOI 10.1103/PhysRevLett.86.1502]</ref>)を用いてごく普通に生成される。 |
|||
しかしこれらの源はいつも効率的であるとは限らず(要求に応じた単一フォトンを実際に得る確率は低い)、しばしば複雑で、実験環境からは適さない。 |
|||
非決定的ふるまいを犠牲にして、これらの問題を克服する別の源が一般的に用いられる。 |
|||
歓迎された単一フォトン源は確率的2フォトン源で、そこからペアが分かれ、1フォトンの検出は残りのフォトンの存在を歓迎する。 |
|||
これらの源はたとえば周期的に分極した[[ニオブ酸リチウム]]([[自発的パラメトリック下方変換]])やシリコン(自発的[[四波混合]])など、通常いくつかの材料の非線形光学作用に依存している。 |
|||
==非古典的ふるまい== |
|||
フォック状態の[[グラウバー-スダルシャンのP表現]]は、これらの状態が純粋に量子力学的な状態であり、古典的対応物は存在しないことを示している。 |
|||
この表現におけるこれらの状態の<math>\scriptstyle\varphi(\alpha) \,</math>{{what|reason=Needs a link or explanation.|date=April 2015}}は[[ディラックのデルタ関数]]の<math>2n</math>次導関数であり、よって古典的な確率分布ではない。 |
|||
==関連項目== |
==関連項目== |
||
2017年4月27日 (木) 14:17時点における版
量子力学においてフォック状態または数状態とは、 粒子(または量子)の数が明確に定義されたフォック空間の要素である量子状態のこと。ソビエトの物理学者ウラジミール・フォックにちなんで名づけられた。
フォック状態は量子力学の第二量子化形式において重要な役割を果たす。
粒子表現は、ポール・ディラックがボース粒子について、パスクアル・ヨルダンとユージン・ウィグナーがフェルミ粒子について詳細に扱ったのが最初である。[1]:35
定義
N個の相互作用の無い同種粒子の多粒子状態を、N個の1粒子状態のテンソル積の和として規定する。 テンソル積は、粒子がフェルミ粒子かボース粒子かによって、下部(underlying)1粒子ヒルベルト空間の交代積または対称積でなければならない。 粒子数が変化する場合は、それぞれの粒子数におけるテンソル積ヒルベルト空間の直和としてフォック空間を構成する。
このとき各1粒子状態における粒子数を規定することで、同じ状態を占有数表示で規定することができる。
kiを下部1粒子ヒルベルト空間における状態の正規直交基底とする。 この基底から、フォック空間での基底である「占有数基底」が導かれる。 フォック空間における状態が占有数基底の要素であるとき、その状態をフォック状態と呼ばれる。
フォック状態は次の重要な基準を満足する。 つまりそれぞれのiにおける状態は、粒子数演算子の固有状態で、基となったi番目の状態kiに対応する。 この固有状態に対応する固有値は、その状態における粒子数を与える。 この基準はフォック状態をほとんど定義している(厳密にはさらに位相因子を選択しなければならない)。
得られたフォック状態は、次のように表す。
この表現におけるとは、i番目の状態kiにおける粒子数である。
i番目の状態における粒子数演算子は、フォック状態に以下のように作用する。
よってフォック状態は、固有値を持つ数演算子の固有状態である [2]:478。
フォック状態は、フォック空間の最も便利な基底を作る。 フォック空間の要素の中で、粒子数が異なる状態の重ね合わせであるものは、数演算子の固有状態ではないためフォック状態ではない。 よってフォック空間の全ての要素が「フォック状態」と呼ばれる訳ではない。
フォック状態の定義より、すなわちフォック状態における粒子数の測定は、常にゆらぎが無く確定値を与える。 よって、
2粒子での例
任意の終状態、2つの同種粒子のフォック状態、演算子について、 次の不可弁別性条件が成り立つ。 [3]:191
- .
よってで、 ボース粒子のときは、フェルミ粒子のときはである。
とは任意であるため、 ボース粒子では、 フェルミ粒子ではである [3]:191。
ここで数演算子ではボース粒子とフェルミ粒子を区別せず、対称性を考慮せずに粒子を数えるだけであることに注意。。 この2種類の粒子の差を見るには、生成消滅演算子と呼ばれる別の演算子が必要となる。
ボース粒子フォック状態
ボース粒子は整数スピンを持つ粒子で「合成した固有状態は交換演算子が作用したとき対称的である」という単純なルールに従う[4]。 たとえばテンソル積表現での2粒子系においては次のようになる。
- 。
ボース粒子の生成消滅演算子
この新しいフォック空間表現では、同じ対称性の性質を表現することができるはずである。 そのためボース粒子の非エルミートな生成消滅演算子を導入し、それぞれ、と表す。 これらの演算子のフォック状態への作用は次の2つの式で与えられる。

生成消滅演算子のエルミート性
生成消滅演算子はエルミート演算子ではない[4]。
生成消滅演算子がエルミート演算子ではない証明 フォック状態において、 よって生成(消滅)演算子のエルミート共役は、自分自身にはならない。よってエルミート演算子ではない。
しかし生成(消滅)演算子のエルミート共役は、消滅(生成)演算子である[5]。:45
演算子の交換関係
ボース粒子系での生成消滅演算子の交換関係は、
ここでは交換子、はクロネッカーのデルタである。
Nボース粒子基底状態
| 粒子数 (N) | ボース粒子基底状態[6]:11 |
|---|---|
| 0 | |
| 1 | ,,,... |
| 2 | ,,,... |
| ... | ... |
具体的なフォック状態への作用
- 真空状態(どの状態にも粒子が無い状態)では、
- 生成演算子を真空状態に作用させることで、どんなフォック状態も作ることができる。
- と表される単一モードフォック状態では、
数演算子の作用
ボース粒子系での数演算子は、次のように与えられる。
これがボース粒子フォック状態に作用すると、次のようになる。
また数演算子はエルミート演算子である。
ボース粒子フォック状態の対称的ふるまい
生成消滅演算子の交換関係により、ボース粒子フォック状態が粒子交換において対称的なふるまいを示す。 ここで2つの状態間の粒子の交換は、ある状態でのある粒子を消滅させ、別の状態での粒子を生成させることで行われる。 フォック状態 から出発して状態から状態への粒子をシフトさせたい場合は、交換関係よりであるため、
よってボース粒子フォック空間は交換演算子の作用において対称的である。
フェルミ粒子フォック空間
フェルミ粒子の生成消滅演算子
フェルミ粒子の反対称的なふるまいを保持するために、フェルミ粒子の非エルミートな生成消滅演算子を導入する。 フェルミ粒子フォック状態 に生成演算子を次のように作用させる。
消滅演算子は次のように作用する。
これら2つの演算子の作用は反対称的に行われる(後述)。
演算子の交換関係
フェルミ粒子系における生成消滅演算子の反交換関係は、
ここで は反交換子、はクロネッカーのデルタである。これらの反交換関係は、フェルミ粒子フォック状態の反対称的なふるまいを表すために用いられる。
数演算子の作用
フェルミ粒子の数演算子は次のように与えられる。
これがフェルミ粒子フォック状態に作用すると、
最大占有数
生成消滅演算子や数演算子の作用はボース粒子の場合と同じであるように見えるが、フェルミ粒子フォック状態の最大占有数から違いが生じる。 上述の2つのフェルミ粒子の例を拡張し、 次のように置換演算子のある特定の和を固有ケットのテンソル積に適用することで、 フェルミ粒子フォック状態が得られることをまず確かめておかなければならない。
- [7]:16
この行列式はスレーター行列式と呼ばれる[要出典]。 もしいかなる1粒子状態も同じであればスレーター行列式の2つの行は同じであり、よって行列式は0になる。 よって2つの同種フェルミ粒子は同じ状態を占めるはずがない。 よっていかなる単一状態の占有数も0または1のどちらかである。 フェルミ粒子フォック状態に関連する固有値は0または1である。
Nフェルミ粒子基底状態
| 粒子数 (N) | フェルミ粒子基底状態[6]:11 |
|---|---|
| 0 | |
| 1 | ,,,... |
| 2 | ,,,... |
| ... | ... |
具体的なフォック状態への作用
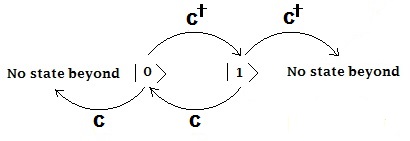
- で表される単一モードフェルミ粒子フォック状態では、
- つまりいかなる状態でも最大占有数は1で、1個以上のフェルミ粒子は同じ状態を占有できない。
- で表される単一モードフェルミ粒子フォック状態において、
- つまり粒子数は0以下になれない。
- で表される多重モードフェルミ粒子フォック状態では、
ここでは、ヨルダン-ウィグナーストリングと呼ばれ、含まれる1粒子状態の順序に依存し、全ての前に来る状態のフェルミ粒子占有数を足し合わせる。[5]:88
フェルミ粒子フォック状態の反対称的なふるまい
交換演算子のもとでのフェルミ粒子状態の反対称的な振る舞いは、反交換関係によるものである。 ここでは2つの状態間の粒子の交換は、ある状態のある粒子を消滅させ、別の粒子を生成させることで行われる。 フォック状態から出発して状態から状態 へ粒子をシフトさせたい場合、反交換関係よりであるため、
しかし、
よってフェルミ粒子フォック状態は、交換演算子の作用のもとでは反対称的にふるまう。
フォック状態は一般的にエネルギー固有状態では無い
第二量子化理論では、ハミルトニアン密度関数は次のように与えられる。
- [3]:189
全ハミルトニアンは、次のように与えられる。
自由粒子のシュレーディンガー方程式[3]:189 は、
この解は直交性を満たす。
また消滅演算子をとして、次の関係がある。
よって、
相互作用しない粒子においてのみ、とが交換する。しかし一般の場合にはこれらは交換しない。 相互作用しない粒子では、
これらが交換しない場合、ハミルトニアンは上述の表現を持たない。 よって一般的にフォック状態は系のエネルギー固有状態ではない。
真空ゆらぎ
真空状態またはは最低エネルギーの状態で、との期待値はこの状態では0になる。
電磁場とベクトルポテンシャルは同じ一般形のモード展開を持つ。
これらの場の演算子の期待値が真空状態では0になることを見るのは簡単である。
しかし、これらの場の演算子の二乗の期待値は0ではないことを示すことができる。 このように0アンサンブル平均についての場におけるゆらぎが存在する。 これらの真空ゆらぎは、量子光学におけるラムシフトなど多くの興味深い現象の原因となる。
多重モードフォック状態
多重モード場におけるそれぞれの生成消滅演算子は、それ自身のモードに作用する。 たとえばとは、にだけ作用する。 異なるモードに対応する演算子はヒルベルト空間の異なる部分空間に作用するため、全体の場は全てのモードにわたる の直積である。
生成消滅演算子の多重モード状態への作用は、それら自身のモードの数状態を上昇または下降させるだけである。
ここで各モードの数演算子の和である、場の全数演算子を定義する。
多重モードフォック状態は全数演算子の固有ベクトルであり、固有値は全てのモードの全占有数である。
相互作用しない粒子では、数演算子とハミルトニアンは互いに交換し、よって多重モードフォック状態は多重モードハミルトニアンの固有状態になる。
単一フォトン状態の源
単一フォトンは、シングルエミッター(原子、窒素-空孔中心[8]、 量子ドット[9])を用いてごく普通に生成される。 しかしこれらの源はいつも効率的であるとは限らず(要求に応じた単一フォトンを実際に得る確率は低い)、しばしば複雑で、実験環境からは適さない。 非決定的ふるまいを犠牲にして、これらの問題を克服する別の源が一般的に用いられる。 歓迎された単一フォトン源は確率的2フォトン源で、そこからペアが分かれ、1フォトンの検出は残りのフォトンの存在を歓迎する。 これらの源はたとえば周期的に分極したニオブ酸リチウム(自発的パラメトリック下方変換)やシリコン(自発的四波混合)など、通常いくつかの材料の非線形光学作用に依存している。
非古典的ふるまい
フォック状態のグラウバー-スダルシャンのP表現は、これらの状態が純粋に量子力学的な状態であり、古典的対応物は存在しないことを示している。 この表現におけるこれらの状態の[要説明]はディラックのデルタ関数の次導関数であり、よって古典的な確率分布ではない。
関連項目
参考文献
- ^ Friedrichs, K. O. (1953). Mathematical aspects of the Quantum Theory of Fields. Interscience Publishers. ASIN B0006ATGK4
- ^ Mandel, Wolf (1995). Optical coherence and quantum optics. Cambridge University Press. ISBN 0521417112
- ^ a b c d Gross, Franz (1999). Relativistic Quantum Mechanics and Field Theory. Wiley-VCH. ISBN 0471353868
- ^ a b c d e f g h i j k l m “Quantum Mechanics 1 Lecture Notes on Identical Particles, TIFR, Mumbai”. Template:Cite webの呼び出しエラー:引数 accessdate は必須です。
- ^ a b Altland, Alexander, Simons, Ben (2006). Condensed Matter Field Theory. Cambridge University Press. ISBN 0521769752
- ^ a b Bruus, Flensberg (2003). Many-Body Quantum Theory in Condensed Matter Physics: An Introduction. OUP Oxford. ISBN 0198566336
- ^ Schwabl, Hilton, Lahee (2008). Advanced Quantum Mechanics. Springer. ISBN 3540850619
- ^ C. Kurtsiefer, S. Mayer, P. Zarda, Patrick and H. Weinfurter, (2000), "Stable Solid-State Source of Single Photons", Phys. Rev. Lett. 85 (2) 290--293, doi 10.1103/PhysRevLett.85.290
- ^ C. Santori, M. Pelton, G. Solomon, Y. Dale and Y. Yamamoto (2001), "Triggered Single Photons from a Quantum Dot", Phys. Rev. Lett. 86 (8):1502--1505 DOI 10.1103/PhysRevLett.86.1502
外部リンク
- Vladan Vuletic of MIT has used an ensemble of atoms to produce a Fock state (a.k.a. single photon) source (PDF)
- Produce and measure a single photon state (Fock state) with an interactive experiment QuantumLab


























![{\displaystyle [b_{i}^{\,},b_{j}^{\dagger }]\equiv b_{i}^{\,}b_{j}^{\dagger }-b_{j}^{\dagger }b_{i}^{\,}=\delta _{ij},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cddd93acb76f64dfd118e4d99025c712d12760f9)
![{\displaystyle [b_{i}^{\dagger },b_{j}^{\dagger }]=[b_{i}^{\,},b_{j}^{\,}]=0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4da7a074faa6df4a260ca9e8fb71c15fb9809657)
![{\displaystyle [\ \ ,\ \ ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53965cb2f0bcd587b309dad04b1fed4736a0d2ea)







































































