ガロア理論の基本定理
数学において、ガロア理論の基本定理 (英: fundamental theorem of Galois theory) とは、ある種の体の拡大がなす構造を記述する結果である。
定理の最も基本的な主張は「体の有限次ガロア拡大 E/F が与えられると、その中間体とガロア群 Gal(E/F) の部分群の間に一対一対応が存在する」ことである。(中間体とは、F ⊆ K ⊆ E を満たす体のことを言う、それらを E/F の部分拡大と言う。)この定理は拡大体 E/F の中間体の分類という難しく聞こえる問題を、ある有限群の部分群を列挙せよというより扱い易い問題へ変換している。
証明
[編集]基本定理の証明は、自明なことではない。通常の扱いで最も重要な点は、与えられた自己同型群により固定された中間体の次元を制御することができるという、エミール・アルティンによる幾分繊細な結果である。ガロア拡大 K/F の自己同型写像は、体 K 上の函数として線型独立である。この事実は、より一般的な事実である指標の線型独立性から従う。
原始元定理を使うかなり簡単な証明もあるが、有限体の場合に異なる(しかしより簡単な)証明をする必要があるため、現代的な取扱いではほとんど用いられない[1]。
抽象的な言葉では「ガロア対応が存在する」と述べられる。その多くの性質は単に形の上でのことであるが、実際の順序集合の同型写像を記述するにはいくらか作業を要する。
対応の明示的な記述
[編集]有限拡大に対し、対応は次のように明示的に述べることができる。
- Gal(E/F) の任意の部分群 H に対し、対応する体は普通 EH と書かれ、これは全ての H の自己同型により固定される E の元の集合である。
- E/F の任意の中間体 K に対し、対応する部分群は、単に Aut(E/K) であり、これは全ての K の元を固定する Gal(E/F) に属する自己同型の集合である。
例えば、一番上の体 E は Gal(E/F) の自明な部分群に対応し、基礎体 F は Gal(E/F) の全体に対応する。
対応の性質
[編集]対応は次のような有益な性質を持っている。
- 包含関係を逆にする(inclusion-reversing)[2]。部分群の包含関係 H1 ⊆ H2 が成り立つことと体の包含関係 EH1 ⊇ EH2 が成り立つこととは同値。
- 拡大次数は包含関係を逆にするという性質と矛盾しない形で群の位数と関係する。具体的には H が Gal(E/F) の部分群であれば |H| = [E : EH] であり |Gal(E/F)/H| = [EH : F] である[3]。
- 体 EH は F の正規拡大(分離拡大の部分拡大は分離的だから、これはガロア拡大というのと同じ)であることと、H が Gal(E/F) の正規部分群であることとは同値である。このとき Gal(E/F) の元の EH への制限は、Gal(EH/F) と商群 Gal(E/F)/H の間の群同型を引き起こす。
例
[編集]
体 K = Q(√2, √3) = Q(√2)(√3) を考える。 K は √2 と √3 を順に添加することで決定されるので、K の各々の元は次のように表すことができる。
ここに a, b, c, d は有理数である。このガロア群 G = Gal(K/Q) は a を固定するような K の自己同型を調べることで決定することができる。ガロア群に属する置換は最小多項式の根の入れ替えだけができるので、そのような自己同型は √2 を √2 もしくは −√2 へ写し、√3 を √3 もしくは −√3 へ写す必要がある。f が √2 と −√2 とを入れ替えるとすると、
となり、g が √3 と −√3 を入れ替えるとすると、
となる。これらは明らかに K の自己同型である。何も変えない恒等写像である自己同型 1 も存在し、f と g の合成も存在し、それらの両方の冪根の符号を変える。
したがって
であり、 G はクラインの四元群に同型である。この群は 5つの部分群を持ち、それらの各々は基本定理から K の部分体と対応する。
- (単位元のみを含む)自明な部分群は、K の全体に対応する。
- 全体 G は、基礎体 Q に対応する。
- 2元からなる部分群 {1, f} は、f が √3 を固定するので部分体 Q(√3) に対応する。
- 2元からなる部分群 {1, g} は、g が √2 を固定するので部分体 Q(√2) に対応する。
- 2元からなる部分群 {1, fg} は、fg が √6 を固定するので部分体 Q(√6) に対応する。
非アーベル的な例
[編集]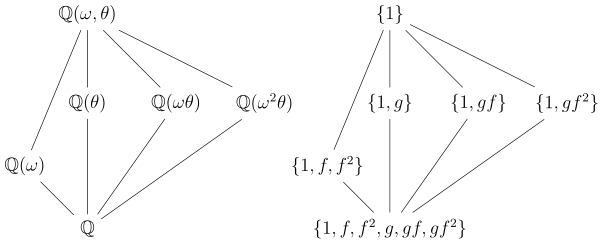
次の例はガロア群がアーベル群でない最も簡単な例である。
Q 上の多項式 x3−2 の分解体 K を考える。すなわち、K = Q (θ, ω) で、ここに θ は 2 の立方根であり、ω は 1 の立方根である(が 1 ではない)。例えば、K を複素数の中の体と考えると、θ として 2 の実立法根、ω として
が取れる。ガロア群 G = Gal(K/Q) は 6 つの元をもち、3つの対象の置換群と同型である。G は(たとえば)2つの自己同型—— f と g とする ——により生成され、それらは次の θ と ω への作用により定められる。
したがって
である。
G の部分群と対応する部分体は次のようになる。
- いつものように全体 G は基礎体 Q に対応し、自明な群 {1} は K 全体に対応する。
- 位数 3 の群、{1, f, f2} が唯一、存在する。対応する部分体は Q(ω) であり、これは Q 上、次数 2 であり(ω 最小多項式は x2 + x + 1 )、G の指数 2 の G の部分群であるという事実に対応している。また、この部分群は正規部分群で、Q 上で正規な体であるという事実に対応している。
- 位数 2 の部分群が 3個存在し、{1, g}, {1, gf}, {1, gf2} で、これらがそれぞれ 3つの部分体 Q(θ), Q(ωθ), Q(ω2θ) に対応している。3つの部分体は Q 上、次数 3 の部分体であり、指数 3 をもつ G の部分群に対応している。注意すべきは、部分群が G で正規部分群ではなく、この事実は部分体は Q 上、ガロア的になっていないという事実に対応している。例えば、Q(θ) は多項式 x3−2 の根を一つしか持っていないので、Q 上、正規ではありえない。
応用
[編集]この定理は拡大体 E/F の中間体の分類という難しく聞こえる問題を、ある有限群の部分群を列挙せよというより扱い易い問題へ変換している。
例えば、一般の五次方程式は冪根によって解けない(アーベル-ルフィニの定理を参照)ことを証明するため、まず最初に、冪根拡大(α を F のある元の n 乗根としたときに F(α) となるような拡大)により問題を言い換え、この基本定理を使い、冪根拡大の問題を直接対応できる群の問題へ変換する。
クンマー理論と類体論のような理論は、この基本定理から予想することができる。
無限次拡大の場合
[編集]この基本定理には、正規拡大であり分離拡大である無限次代数拡大へ適用できるバージョンも存在する。これには、ガロア群にクルル位相というある位相構造を定義することが必要で、閉集合である部分群だけが上記の対応と関連している。
脚注
[編集]参考文献
[編集]- Cox, David A. (2012). Galois Theory. Pure and Applied Mathematics (Second ed.). Wiley. doi:10.1002/9781118218457. ISBN 978-1-118-07205-9. MR2919975. Zbl 1247.12006









