「順序集合」の版間の差分
1.114.37.1 (会話) 2013年3月8日 (金) 20:57 へ差し戻し タグ: サイズの大幅な増減 |
Aquamarin456 (会話 | 投稿記録) ここまで大きな編集を行うのでしたらノートで合意を得てください。節まで変更していますし・・・ タグ: サイズの大幅な増減 |
||
| 1行目: | 1行目: | ||
[[数学]]において'''順序集合'''(じゅんじょしゅうごう、{{lang-en-short|''ordered set''}})とは |
|||
[[Image:Hasse diagram of powerset of 3.svg|right|thumb|250px|三元集合 {''x'', ''y'', ''z''} の[[冪集合|部分集合の全体]]を包含関係を順序とする順序集合とみたときの[[ハッセ図]]]] |
|||
「順序」の概念が定義された集合の事で、「順序」とは大小、高低、長短等の序列に関わる概念を抽象化したものである。 |
|||
[[数学]]における('''半''')'''順序集合'''(はん-じゅんじょしゅうごう、{{lang-en-short|[''partially''] ''ordered set'', '''poset'''}})とは整列、序列化、配列、順序付けといった直感的概念を定式化するものである。順序集合は、台となる集合とともに、その集合のある[[元 (数学)|元]]が別の元よりも大きい・小さい、前にある・後にある、上位である・下位であるなどといったことを指示する[[二項関係]]をあわせて考えたものである。 |
|||
ただし順序集合内の2つの元''a''、''b'' に順序関係が定まっている必要はなく、両者が「比較不能」であってもよい。よって''a''、''b'' の関係は「''a'' は''b'' 以上である」、「''b'' は''a'' 以上である」、「''a'' と''b'' は比較不能である」の3通りのいずれかとなる。 |
|||
このような序列をあらわす関係は、一般には集合のふたつの元が必ずしも比較可能でない(ある元の対に対して、その順序ではどちらが大きいとも小さいともいえないということが起こり得る)という事実を反映して'''半順序'''(はんじゅんじょ、{{lang|en|''partial order''}}; 偏順序、部分順序)と呼ばれる。どのふたつの元でも比較できるような特別な順序は'''全順序''' {{lang|en|(total order)}} または'''線型順序''' {{lang|en|(linear order)}} と呼ばれる。 |
|||
比較不能のケースを許容している強調して順序集合の事を'''半順序集合'''(はんじゅんじょしゅうごう、{{lang-en-short|''partially ordered set'', '''poset'''}})ともいう。一方、半順序集合の中で特に比較不能のケースがないものをしないものを'''全順序集合'''(totally ordered set)という。(「半順序」という言葉が「全順序」の対義語ではない事に注意。全順序集合も半順序集合の一種である)。 |
|||
(台となる集合が[[有限集合]]であるような)有限順序集合は、ふたつの元に順序関係があるかどうかを示した[[ハッセ図]]を使えば、視覚化したり部分順序構造を再構成したりすることができる。 |
|||
全順序集合の簡単な例は整数の集合や実数の集合で、通常の大小比較を順序とみなしたものがある。 |
|||
実生活に近いところで言えば、血統的な子孫であるという関係で人間の集まりを考えたりすることは順序集合の例になっている。実際、あるふたりの人は先祖と子孫の関係にあるかもしれないが、そのような関係を持たない組合せもたくさんある。 |
|||
一方、全順序ではない半順序集合の例としては(2つ以上元を含む)集合の冪集合で、包含関係を順序とみなしたものがある。例えば3元集合''P'' ={a,b,c}において{a,b}と{b,c}はいずれも他方を包含していないので''P'' の冪集合は全順序ではない。実生活に近い例では、「AさんはBさんの子孫である」という事を「A<B」という大小関係とみなす事で人間全体の集合を半順序集合とみなせる。AさんとBさんはどちらも他方の子孫でない事もありうる(兄弟同士、叔父と甥、赤の他人等)ので、この順序集合は全順序ではない。 |
|||
== 定義 == |
== 定義 == |
||
全順序集合、半順序集合、およびこれらよりさらに弱い概念である前順序集合の定義を述べる為にまず以下の性質を考える。ここで''P'' は集合であり、「≤」を''P'' 上で定義された[[二項関係]] である。 |
|||
集合 ''A'' 上の('''半''')'''順序'''('''関係''') {{lang|en|(''partial order'')}} とは、 [[反射関係|反射的]] {{lang|en|(reflexive)}} で反対称的 {{lang|en|(antisymmetric)}} かつ[[推移関係|推移的]] {{lang|en|(transitive)}} な ''A'' 上の[[二項関係]]すなわち ''a'', ''b'', ''c'' を ''A'' の任意の元として |
|||
# 反射律: ''a'' ≤ ''a'', |
|||
# 推移律: ''a'' ≤ ''b'' かつ ''b'' ≤ ''c'' ならば ''a'' ≤ ''c'', |
|||
# 反対称律: ''a'' ≤ ''b'' かつ ''b'' ≤ ''a'' ならば ''a'' = ''b'' |
|||
; [[反射関係|反射律]] : <math>\forall a \in P : a \le a</math> |
|||
が成立するような関係 "≤" のことをいう。 |
|||
; [[推移関係|推移律]] : <math>\forall a, b, c \in P : a \le b \land b \le c \to a \le c</math> |
|||
; 反対称律 : <math>\forall a, b \in P : a \le b \land b \le a \to a = b</math> |
|||
; 全順序律 : <math>\forall a, b \in P : a \le b \lor b \le a</math> |
|||
「≤」が全順序律を満たさない場合、「''a'' ≤ ''b''」でも「''b'' ≤ ''a''」でもないケースがある。このような第三のケースにあるとき''a'' と''b''は'''比較不能'''であるという。 |
|||
反射律と推移律が成り立つ二項関係は[[前順序]](preorder)と呼ばれる。つまり、半順序は反対称的な前順序と言い表すこともできる。 |
|||
=== {{anchors|前順序|半順序|全順序|前順序集合|半順序集合|全順序集合}}前順序・半順序・全順序 === |
|||
推移律と反対称律によって、半順序関係においてはいわゆる三竦みが起こらないことが保証される。 |
|||
{{mvar|P}} を集合とし、{{math|≤}} を {{mvar|P}} 上で定義された[[二項関係]] とする。 |
|||
* {{math|≤}} が反射律と推移律を満たすとき {{math|≤}} を {{mvar|P}} 上の'''前順序'''という。 |
|||
* 前順序な {{math|≤}} が反対称律をも満たすとき {{math|≤}} を {{mvar|P}} 上の'''半順序'''という。 |
|||
* 半順序な {{math|≤}} が全順序律をも満たすとき {{math|≤}} を {{mvar|P}} 上の'''全順序'''という。 |
|||
{{math|≤}} が前順序である {{math|(''P'', ≤)}} を'''前順序集合'''という。同様に {{math|≤}} が半順序なら {{math|(''P'', ≤)}} は'''半順序集合'''、全順序なら {{math|(''P'', ≤)}} は'''[[全順序集合]]'''である。また集合 {{mvar|P}} は {{math|(''P'', ≤)}} の'''[[台 (数学)|台]]''' {{en|(support)}} と呼ばれる。紛れがなければ {{math|≤}} を省略し、{{mvar|P}} の事を(いずれかの意味で)順序集合という。 |
|||
半順序 ≤ をもつ集合 ''A'' を('''半''')'''順序集合''' {{lang|en|([''partially''] ''ordered set'')}} あるいは簡単に'''ポセット''' {{lang|en|(''poset'')}} と呼び、(''A'', ≤) あるいは紛れのおそれの無い場合は台集合と同じく ''A'' で表す。 |
|||
順序集合 {{math|(''P'', ≤)}} に対し、{{math|≤}} を台 {{mvar|P}} 上の'''順序関係'''ともいう。 |
|||
半順序集合 ''P'' のふたつの元 ''a'', ''b'' に対し、''a'' ≤ ''b'' または ''b'' ≤ ''a'' のいずれか(あるいは両方)が成り立つとき、''a'' と ''b'' は'''比較可能''' {{lang|en|(''comparable'')}} であるといい、そうでないとき'''比較不能''' {{lang|en|(''incomparable'')}} であるという。順序集合 (''A'', ≤) が条件 |
|||
なお多くの数学の分野では半順序集合を主に扱うので、単に'''順序'''あるいは'''順序集合'''といった場合はそれぞれ半順序、半順序集合を意味する場合が多いが、分野によっては、主な対象が半順序集合でなく前順序集合や全順序集合である場合があり、そのような分野では前順序集合や全順序集合の意味で「順序集合」という言葉が用いられることがあるので注意が必要である。 |
|||
* 完全律 (totalness): ''A'' の任意の元 ''a'', ''b'' について比較可能である |
|||
を満たすとき、順序 ≤ は'''全順序''' {{lang|en|(''total order'')}} または'''線型順序''' {{lang|en|(linear order)}} であるといい、順序集合 ''A'' は'''全順序集合''' {{lang|en|(''totally ordered set'')}} または'''[[鎖 (数学)|鎖]]''' {{lang|en|(''chain'')}} と呼ぶ。また、任意のふたつの元が比較不能であるような半順序集合を'''[[反鎖]]''' {{lang|en|(''anti-chain'')}} という。 |
|||
上では順序を記号 {{math|≤}} で表したが、必ずしもこの記号で表現する必要はない。 |
|||
全順序集合を単に順序集合といい、全順序でないものを特に半順序集合と呼ぶ流儀もある。 |
|||
実数の大小を表す記号 {{math|≤}} と区別する為、順序の記号として <math>\prec</math> や <math>\ll</math> を使うこともある。 |
|||
全順序の事を'''線型順序'''ともいい、'''全順序集合'''のことを'''鎖'''と呼ぶこともある。また半順序集合の部分集合 {{mvar|A}} で {{mvar|A}} の任意の相異なる二元が比較不能であるものを'''{{仮リンク|反鎖|en|Anti-chain}}'''という。 |
|||
== 狭義の順序 == |
|||
いくつかの文脈では、上で述べた半順序を'''広義''' {{lang|en|(''non-strict'')}} の、'''弱い'''意味 {{lang|en|(''weak'')}} の、'''反射的''' {{lang|en|(''reflexive'')}} な半順序と呼び、代わりに、'''狭義''' {{lang|en|(''strict'')}} のあるいは'''非反射的''' {{lang|en|(''irreflexive'')}} な半順序 "<" を、[[非反射関係|非反射的]]かつ[[推移関係|推移的]]な、したがって[[非対称関係|非対称]]な二項関係として定めることがある。つまり、半順序集合 ''P'' における狭義の順序を、''a'', ''b'', ''c'' は ''P'' の任意の元として |
|||
半順序集合の元 {{mvar|a}} が他の元 {{mvar|b}} によって{{仮リンク|被覆関係|en|Covering relation|label='''被覆される'''}} {{math|''a'' <: ''b''}} とは、{{mvar|a}} は {{mvar|b}} よりも'''真に小さく'''、かつそれらの間に別の元が入ることはないこと(後述する狭義の記号を使って書けば {{math|''a'' < ''b''}} かつ任意の {{mvar|c}} に対して {{math|''a'' < ''c'' < ''b''}} が偽となること)をいう。 |
|||
* 非反射性: ¬(''a'' < ''a''); |
|||
* 非対称性: ''a'' < ''b'' ならば ¬(''b'' < ''a''); |
|||
* 推移性: ''a'' < ''b'' かつ ''b'' < ''c'' ならば ''a'' < ''c'' |
|||
によって定める。広義の順序と狭義の順序との間には[[全単射|一対一対応]]が存在する。 "≤" を広義の順序とすると、対応する狭義の順序 "<" は |
|||
=== 順序集合の例 === |
|||
: <math>a < b \iff (a \le b \and a \ne b)</math> |
|||
で与えられる反射的簡約 {{lang|en|(reflexive reduction)}} である。逆に、狭義の半順序 "<" に対応する広義の半順序 "≤" は |
|||
: <math>a \le b \iff a < b \or a = b</math> |
|||
で与えられる[[反射的閉包]]である。このような対応関係があることは、半順序を表すのに "≤" を用いる理由となっている。 |
|||
狭義の順序は広義のそれよりも直接的に[[非循環有向グラフ]]に対応するという点で有用である。任意の狭義半順序は非循環有向グラフであり、非循環有向グラフの[[推移的閉包]]は狭義半順序集合、したがってふたたび非循環有向グラフとなる。 |
|||
== 例 == |
|||
* 都道府県の集合に人口の大小で順序を定めると前順序集合になる。特に人口の等しい都道府県が無ければ全順序集合になる。 |
|||
* [[自然数]]全体の集合 '''N'''、[[整数]]全体の集合 '''Z'''、[[有理数]]全体の集合 '''Q'''、[[実数]]全体の集合 '''R''' は通常の代数的な大小関係によって全順序集合になるが、[[複素数]]はそうではない。複素数全体の集合 '''C''' に '''R''' × '''R''' としての[[辞書式順序]]を定めたものは全順序集合であるが、この順序は複素数の乗法とは両立しない。 |
* [[自然数]]全体の集合 '''N'''、[[整数]]全体の集合 '''Z'''、[[有理数]]全体の集合 '''Q'''、[[実数]]全体の集合 '''R''' は通常の代数的な大小関係によって全順序集合になるが、[[複素数]]はそうではない。複素数全体の集合 '''C''' に '''R''' × '''R''' としての[[辞書式順序]]を定めたものは全順序集合であるが、この順序は複素数の乗法とは両立しない。 |
||
* [[自然数]]全体の成す集合は整除関係を順序として半順序集合である。 |
* [[自然数]]全体の成す集合は整除関係を順序として半順序集合である。 |
||
| 58行目: | 50行目: | ||
* 半順序集合における順序関係の向きが ''a'' < ''b'' > ''c'' < ''d'' ... というように交互に入れ替わる列を[[フェンス (数学)|フェンス]]と呼ぶ。 |
* 半順序集合における順序関係の向きが ''a'' < ''b'' > ''c'' < ''d'' ... というように交互に入れ替わる列を[[フェンス (数学)|フェンス]]と呼ぶ。 |
||
== |
== 逆順序、狭義の順序、双対順序 == |
||
写像 ''f'': ''A'' → ''B'' は ''A'' の任意の元 ''a'', ''b'' について |
|||
: ''a'' ≤ ''b'' ならば ''f''(''a'') ≤ ''f''(''b'') を満たすとき'''順序を保つ'''写像といわれる。 |
|||
: ''a'' ≤ ''b'' ならば ''f''(''a'') ≥ ''f''(''b'') を満たすとき'''順序を逆にする'''写像といわれる。 |
|||
上で述べた順序関係「≤」は直観的には左辺が右辺よりも「小さい、もしくは等しい」事を意味しているが、逆に左辺が右辺よりも「大きい、もしくは等しい」順序関係や等しい事を許容しない順序関係を考える事もできる。 |
|||
実変数実数値の関数で単調増大なものは順序を保つ写像、単調減少なものは順序を逆にする写像となっていることから、順序を保つ写像と順序を逆にする写像を総称して'''単調写像'''ということがある。 |
|||
=== 逆順序 === |
|||
順序を保つ写像 ''f'': ''A'' → ''B'' が全単射であっても、逆写像 ''f''<sup>−1</sup> は順序を保つとは限らないが(ただし、''A'',''B'' が全順序集合のときは ''f''<sup>−1</sup> は順序を保つ)、逆写像 ''f''<sup>−1</sup> も順序を保つとき、''f'' は '''順序[[準同型|同型写像]]'''あるいは単に'''順序同型'''と呼ばれる。また、''A'' と ''B'' は'''順序同型である'''という。 |
|||
「大きい、もしくは等しい」事を意味する順序関係は「≤」の'''逆順序'''と呼ばれ、 |
|||
順序同型な 2 つの順序集合は、個々の要素は異なっても順序集合として同じ"形"をしていると言える。そこで、同じ"形"をした順序集合たちにその"形"を表す何かを割り当て、個々の要素の違いを無視した構造のみに注目して順序集合を考察をすることが考えられる。このように各順序集合に割り当てられたものを'''順序型'''と呼ぶ。 |
|||
{{main|順序型}} |
|||
: <math>a \ge b \iff b \le a</math> |
|||
== 直積集合上の順序 == |
|||
ふたつの半順序集合(の台集合)の[[直積集合]]上の半順序としては次の三種類が考えられる。 |
|||
* [[辞書式順序]]: <math>(a, b) \le (c, d) \iff a < c \or (a = c \and b \le d)</math> |
|||
* [[積順序]]: <math>(a, b) \le (c, d) \iff a \le c \and b \le d</math> |
|||
* <math>(a, b) \le (c, d) \iff (a < c \and b < d) \or (a = c \and b = d)</math> |
|||
により定義される。 |
|||
最後の順序は対応する狭義全順序の[[関係の直積|直積]]の反射閉包である。これらの三種類の順序はいずれもふたつよりも多くの半順序集合の直積に対しても同様に定義される。 |
|||
=== 狭義の順序 === |
|||
[[体 (数学)|体]]上の[[順序線型空間]]に対してこれらの構成を適用すれば、結果として得られる順序集合はいずれもふたたび順序線型空間となる。 |
|||
一方、等しい事を許容しない順序は'''狭義の(半)順序'''と呼ばれ、以下のように定義される: |
|||
== 逆順序・双対順序 == |
|||
: <math>a < b \iff (a \le b \and a \ne b)</math> ...(1) |
|||
半順序関係 "≤" の逆 {{lang|en|(inverse, converse, opposite)}} "≥" とは |
|||
: <math>x \ge y \iff y \le x</math> |
|||
を満足する関係である。半順序の逆は、反射的、推移的かつ反対称な関係であるから、それ自身が半順序である。半順序集合 (''P'', ≤) の'''双対順序集合''' {{lang|en|(''order dual'')}} とは、台集合はもとの半順序集合のそれと同じものとし、もとの半順序の逆を順序関係として入れた半順序集合 (''P'', ≥) を言う。"≥" に対する非反射的順序 ">" も、"≤" に対する "<" と同様に定義される。 |
|||
狭義の逆順序「>」も自然に定義される。 |
|||
与えられた集合上の四つの関係 "≤", "<", "≥", ">" は、そのうちのいずれでも一つ与えられれば、他の三つはそれから一意的に決定することができる。 |
|||
狭義の順序「<」の対義語として、等しい事も許容する順序「≤」の事を'''広義の(半)順序'''(もしくは'''弱い'''意味 {{lang|en|(''weak'')}} の(半)順序、'''反射的''' {{lang|en|(''reflexive'')}} な(半)順序)という。 |
|||
一般に、半順序集合のふたつの元 ''x'', ''y'' に対して、 |
|||
* ''x'' < ''y'', |
|||
* ''x'' = ''y'', |
|||
* ''x'' > ''y'', |
|||
* ''x'' と ''y'' は比較不能 |
|||
という互いに排他的な四つの条件のうち、いずれかひとつだけが成り立つ。[[全順序集合]]に対しては、ふたつの元は常に比較可能だから、この最後の条件は無視してよい(このとき、[[三分法 (数学)|三分法]]が成り立つという)。 |
|||
(1)式で定義された「<」を「≤」の'''反射的簡約''' {{lang|en|(reflexive reduction)}} という。 |
|||
== 順序集合の極値 == |
|||
順序集合の「最大」や「最小」に関する概念にはいくつかの種類がある。 |
|||
「≤」が半順序であるとき、その反射的簡約「<」は任意の''a'', ''b'', ''c'' ∈ ''P'' に対して以下を満たす: |
|||
順序集合の空でない部分集合 ''A'' について、''A'' の任意の元 ''a'' に対して ''a'' ≤ ''b'' が成り立つような ''b'' を ''A'' の'''上界'''(じょうかい、upper bound)という。上界が存在するとき、集合 ''A'' は'''上に有界'''であるという。また、''A'' の任意の元 ''a'' に対して ''b'' ≤ ''a'' が成り立つような ''b'' を ''A'' の'''下界'''(かかい、lower bound)という。下界が存在するとき、集合 ''A'' は'''下に有界'''であるという。上下に有界であるとき、単に'''[[有界]]である''' (bounded) という。 |
|||
; 非反射性 : ¬(''a'' < ''a''); |
|||
''A'' のある元 ''s'' に対して、''s'' ≤ ''a'' となる ''A'' の元 ''a'' は常に ''s'' = ''a'' となるとき、''s'' を'''極大元'''(きょくだいげん、 maximal element)という。 |
|||
; 非対称性 : ''a'' < ''b'' ならば ¬(''b'' < ''a''); |
|||
また、''A'' のある元 ''s'' に対して、''a'' ≤ ''s'' となる ''A'' の元 ''a'' は常に ''s'' = ''a'' となるとき、''s'' を'''極小元'''(きょくしょうげん、minimal element)という。 |
|||
; 推移性 : ''a'' < ''b'' かつ ''b'' < ''c'' ならば ''a'' < ''c'' |
|||
以上では広義の順序からスタートして狭義の順序を定義したが、逆に上の三性質を満たすものを狭義の順序として定義し、広義の順序を |
|||
''A'' のある元 ''m'' が任意の ''A'' の元 ''a'' に対して ''a'' ≤ ''m'' を満たすとき、''m'' を ''A'' の'''最大元'''(さいだいげん、maximum element)といい、max ''A'' と書く。また、''A'' のある元 ''m'' が任意の ''A'' の元 ''a'' に対して ''m'' ≤ ''a'' を満たすとき、''m'' を ''A'' の'''最小元'''(さいしょうげん、minimum element)といい、min ''A'' と書く。 |
|||
: <math>a \le b \iff a < b \or a = b</math> ...(2) |
|||
最大元や最小元は[[高々 (数学)|高々]]一つしかないことが、順序の公理の 3 番目(反対称律)から分かる。最大元は極大元になるが、この逆は正しくない。''A'' はいくつもの異なる極大元を持つかもしれない。 |
|||
により定義する事もできる。 |
|||
上界の集合の最小元(つまり、最小の上界)のことを、'''上限'''(じょうげん、least upper bound, supremum)といい、sup(''A'') と書く。また、下界の集合の最大元(つまり、最大の下界)のことを、'''下限'''(かげん、greatest lower bound, infimum)といい、inf(''A'') と書く。 |
|||
この場合、(2)式で定義された「≤」を「<」の{{仮リンク|反射閉包|en|Binary relation#Operations on binary relations}}という。 |
|||
「<」が前述の3条件を満たせば反射閉包「≤」が半順序である事を簡単に示す事ができる。 |
|||
<!-- |
|||
全順序集合は比較不能であるということが起きないような半順序集合を言い、従って任意の二元は比較可能であり、このとき{{仮リンク|三分法 (数学)|label=三分律|en|Trichotomy (mathematics)}}が成り立つという。 |
|||
--> |
|||
=== 双対順序集合 === |
|||
''A'' が最大元 ''M'' を持てば、''M'' は ''A'' の上限になる。また、''A'' が最小元 ''m'' を持てば、''m'' は ''A'' の下限になる。 |
|||
{{math|(''P'' , ≤)}}を順序集合とするとき、''P'' 上の二項関係「<math>\preccurlyeq</math>」を |
|||
: <math> a \preccurlyeq b \iff b \le a</math> |
|||
* 自然数の間に順序 ''a'' ≤ ''b'' を ''a'' | ''b''(''a'' は ''b'' の[[約数]])で定義する。集合 {''a'', ''b''} の上界、下界はそれぞれ ''a'' と ''b'' の公倍数、公約数であり、上限、下限はそれぞれ最小公倍数、最大公約数である。{1, 2, ..., 10} の極大元は 6, 7, 8, 9, 10 であり、最大元は存在しない。最小元は 1 である。 |
|||
* 集合 ''S'' を ''S'' = {''m'' | ある自然数 ''n'' が存在して ''m'' = 2<sup>''n''</sup>} で定義して上と同じ順序を考えると、これは全順序集合になる。写像 ''f'': ''S'' → '''N''' を ''f''(2<sup>''n''</sup>) = ''n'' で与えると、これは順序同型になる。ただし、値域の自然数の順序には普通の大小関係を考える。 |
|||
* ''S'' をある集合とし、その[[べき集合]] 2<sup>''S''</sup> の間に包含関係による順序を考える。''A'', ''B'' を ''S'' のある部分集合とすると、{''A'', ''B''} の上限、下限はそれぞれ ''A'' ∪ ''B''、''A'' ∩ ''B'' である。 |
|||
* ある環の自明でない[[イデアル]]全体の集合に包含関係による順序を考える。極大イデアルはこの集合の極大元である。 |
|||
と定義する(すなわち「<math>\preccurlyeq</math>」は「≤」の逆順序を順序とみなしたものである)。すると、「<math>\preccurlyeq</math>」も''P'' 上の順序になっている事が簡単に示せる。<math>(P,\preccurlyeq)</math>を{{math|(''P'' , ≤)}}の'''双対順序集合'''という。 |
|||
== 整列集合 == |
|||
{{main|整列集合}} |
|||
順序集合は、その任意の空でない部分集合が最小元を持つとき'''整列集合''' (well-ordered set) であるという。また、その順序を'''整列順序''' (well-order) という。定義からすぐに「整列集合は全順序集合である」ということが分かる。実際、任意の二つの元 ''a'', ''b'' をとってきたとき、その二つの元のなす集合 {''a'', ''b''} にも最小元があるから、''a'' ≤ ''b'' か ''b'' ≤ ''a'' のどちらかが成り立つ。これは全順序であるということに他ならない。 |
|||
双対順序集合はその定義<math>(P,\preccurlyeq)</math>よりもとの順序集合{{math|(''P'' , ≤)}}とは大小が逆転している。したがって{{math|(''P'' , ≤)}}における上限、極大元、最大元は<math>(P,\preccurlyeq)</math>ではそれぞれ下限、極小元、最小元になる。 |
|||
* 自然数全体の集合 '''N''' は大小関係によって整列集合になる。 |
|||
* 普通の大小関係において整数全体の集合 '''Z'''、有理数全体の集合 '''Q'''、実数全体の集合 '''R''' はそうではない。 |
|||
* '''Z''' は 0 < -1 < 1 < -2 < 2 < -3 < 3 < … と順序を定めると整列集合になる。 |
|||
* '''Q''' や '''R''' では(特に '''R''' では)、このような簡単な修正ではうまく行かない。 |
|||
==ハッセ図== |
|||
しかし、[[選択公理]]を仮定すると、次の'''整列可能定理''' (well-ordering theorem、単に整列定理、[[エルンスト・ツェルメロ|ツェルメロ]]の整列定理ともいう)が証明できる。 |
|||
[[Image:Hasse diagram of powerset of 3.svg|right|thumb|150px|三元集合 {''x'', ''y'', ''z''} の[[冪集合|部分集合の全体]]を包含関係を順序とする順序集合とみたときの[[ハッセ図]]]] |
|||
:''任意の集合は整列集合となるように順序を定めることができる。'' |
|||
逆に、整列可能定理を仮定して選択公理を証明することもできるので、整列可能定理は選択公理と同値であり、さらには[[ツォルンの補題]]などとも同値である。 |
|||
''P'' を有限集合とし、「<」を''P'' 上の狭義の半順序とするとき、以下のようにして''P'' を自然に[[グラフ理論|単純有向グラフ]]とみなせる: |
|||
== 線型順序拡大 == |
|||
: 頂点:''P''の元 |
|||
[[全順序]] ''T'' が半順序 ''P'' の[[線型拡大]](あるいは線型拡張)であるとは、''P'' において ''x'' ≤ ''y'' であるような二元については ''T'' においてもなお ''x'' ≤ ''y'' となっているときにいう。任意の半順序は全順序に拡張することができる(順序拡大原理<ref>{{cite book |last=Jech |first=Thomas |title=The Axiom of Choice |year=2008 |origyear=originally published in 1973 |publisher=[[Dover Publications]] |isbn=0-486-46624-8}}</ref>)。 |
|||
: ''a'' ∈ ''P'' から ''b'' ∈ ''P'' への辺がある⇔ {{math|''a'' < ''b''}} であり、しかも{{math|''a'' < ''c'' < ''b''}}を満たす''c'' ∈ ''P''が存在しない。(すなわち''b'' は''a'' を被覆している)。 |
|||
この有向グラフを図示したものを'''[[ハッセ図]]'''という。 |
|||
[[計算機科学]]において、半順序の線型拡張を求めるアルゴリズムは[[位相ソート]] {{lang|en|(topological sorting)}} と呼ばれる。 |
|||
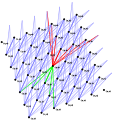
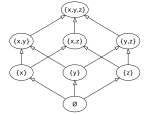
右に示した図がハッセ図の例である。この図では三元集合 {''x'', ''y'', ''z''}の [[冪集合|部分集合の全体]]を包含関係を順序とする順序集合とみなしたものをハッセ図として表している。 |
|||
ハッセ図を用いると、順序関係に関する基本的な概念が図示できる。 |
|||
例えばこの図で {''x''} と {''x'',''y'',''z''} は比較可能だが、{''x''} と {''y''} は比較不能である。 |
|||
また[[一元集合]]の族 {{math|{{''x''}, {''y''}, {''z''}}}}は反鎖である。 |
|||
さらに{''x''} は {''x'',''z''} によって被覆されるが、{''x'',''y'',''z''} には被覆されない。 |
|||
なお、有限半順序集合から前述の方法で作ったグラフは閉路を持たない。 |
|||
逆に{{math|(''V'' , ''E'' )}}を閉路を持たない有限な単純有向グラフとすると、''V'' 上に以下の順序を入れる事で''V'' を半順序集合とみなせる: |
|||
: {{math|''a'' < ''b''}} ⇔ ''a'' から''b'' への道がある |
|||
したがって有限半順序集合は閉路を持たない有限な単純有向グラフと自然に同一視できる。 |
|||
== {{anchors|上界|下界|上限|下限|最大|最小|極大|極小}}上界、最大、極大、上限、上方集合== |
|||
{{mvar|P}} を[[#半順序集合|半順序集合]]とし、{{mvar|A}} をその[[部分集合]]とし、{{mvar|x}} を {{mvar|P}} の[[元 (数学)|元]]とする。 |
|||
このとき上界、最大、極大、上限の概念、およびこれらの[[双対|双対概念]]である下界、最小、極小、下限は以下のように定義される: |
|||
=== 定義 === |
|||
* {{mvar|x}} が {{mvar|A}} の'''上界'''([[Wikt:resp.|resp.]] '''下界'''): {{math|∀''y'' ∈ ''A'' : ''y'' ≤ ''x'' (resp. ''y'' ≥ ''x'')}} |
|||
* {{mvar|x}} が {{mvar|A}} の'''最大元'''(resp. '''最小元'''): {{mvar|x}} は {{mvar|A}} の元でしかも {{mvar|x}} は {{mvar|A}} の上界(resp. 下界)である |
|||
* {{mvar|x}} が {{mvar|A}} の'''極大元'''(resp. '''極小元'''): {{mvar|x}} は {{mvar|A}} の元でしかも <math>y \gneqq x</math> (resp. <math>y \lneqq x</math>) を満たす {{math|''y'' ∈ ''A''}} が存在しない |
|||
* {{mvar|x}} が {{mvar|A}} の'''上限'''(resp. '''下限'''): {{mvar|x}} は集合{{math|{{(}}''y'' ∈ ''P'' {{!}} ''y''}} は {{mvar|A}} の上界(resp. 下界){{math|{{)}}}} の最小元(resp. 最大元) |
|||
上界および上限の定義において {{mvar|x}} が {{mvar|A}} に必ずしも属さないことには注意が必要である。 |
|||
極大元の概念と最大元の概念は以下の点で異なる。 |
|||
まず {{mvar|x}} が {{mvar|A}} の極大元であるとは、{{mvar|A}} の元は「{{mvar|x}} 以下である」か、もしくは「{{mvar|x}} とは大小が比較不能である」かのいずれかである事を意味する。一方 {{mvar|x}} が {{mvar|A}} の最大元であるとは {{mvar|A}} の元は常に {{mvar|x}} 以下である事を意味する(このとき {{mvar|A}} の元は {{mvar|x}} と比較可能である)。したがって最大元は極大元であるが、極大元は必ずしも最大元であるとは限らない。 |
|||
さらに {{mvar|A}} が {{mvar|P}} の'''{{仮リンク|上方集合|en|upper set}}'''(resp. '''下方集合''')であるとは、任意の {{math|''a'' ∈ ''A'' }} と {{math|''x'' > ''a'' }} (resp. {{math|''x'' < ''a''}}) を満たす任意の {{mvar|P}} の元に対し{{math|''x'' ∈ ''A'' }} となることをいう。 |
|||
===具体例=== |
|||
{| |
|||
|[[File:Hasse diagram of powerset of 3 no greatest or least.svg|thumb|right|x150px|三元集合の冪集合のハッセ図から最大元と最小元を取り除いたもの。この図の一番上の行にある各元がこの半順序の極大元であり、一番下の行の各元は極小元である。最大元と最小元はない。集合 {x, y} は元の族 {{x}, {y}} に対する上界を与える。]] |
|||
|[[File:Infinite lattice of divisors.svg|thumb|right|x150px|整除性によって順序付けられた非負整数のハッセ図]] |
|||
|} |
|||
[[正整数]]全体の成す集合を整除関係で順序付ける時、{{math|1}} は任意の正整数を割り切るという意味において {{math|1}} は最小元である。しかしこの半順序集合には最大元は存在しない(任意の正整数の倍数としての 0 を追加して考えたとするならば、それが最大元になる)。この半順序集合には極大元も存在しない。実際、任意の元 ''g'' はそれとは異なる例えば 2''g'' を割り切るから ''g'' は極大ではありえない。この半順序集合から最小元である 1 を除いて、順序はそのまま整除関係によって入れるならば、最小元は無くなるが、極小元として任意の[[素数]]をとることができる。この半順序に関して 60 は部分集合 {2,3,5,10} の上界(上限ではない)を与えるが、1 は除かれているので下界は持たない。他方、[[2の冪|{{math|2}} の冪]]全体の成す部分集合に対して {{math|2}} はその下界(これは下限でもある)を与えるが、上界は存在しない。 |
|||
== 写像と順序 == |
|||
順序に関する写像の概念に以下のものがある: |
|||
=== 定義 === |
|||
''S'' 、''T'' を順序集合とし、''f'': ''S'' → ''T'' を写像とする。このとき |
|||
* ''f'': ''S'' → ''T'' が'''順序を保つ'''({{仮リンク|order-preserving|en|order-preserving}}。'''同調''' (''isotone'')とも) とは、任意の ''x'', ''y'' ∈ ''S'' に対して ''x'' ≤ ''y'' ⇒ ''f'' (''x'') ≤ ''f'' (''y'') である事を言う。 |
|||
* ''f'': ''S'' → ''T'' が'''順序を逆にする'''({{仮リンク|order-reversing|en|order-reversing<!-- リダイレクト先の「[[:en:Monotonic function]]」は、[[:ja:単調写像]] とリンク -->}})とは、任意の ''x'', ''y'' ∈ ''S'' に対して ''x'' ≤ ''y'' ⇒ ''f'' (''x'') ≥ ''f'' (''y'') である事を言う。 |
|||
* 上の2つを合わせて[[単調写像|単調]](''monotone'') 写像と言う。 |
|||
* ''f''が'''順序を反映する''' (''order-reflecting'') とは任意の ''x'', ''y'' ∈ ''S'' に対して ''f'' (''x'') ≤ ''f'' (''y'') ⇒ ''x'' ≤ ''y'' であることを言う。 |
|||
* ''f'' が'''{{仮リンク|順序埋め込み|en|order-embedding}}'''であるとは、任意の ''x'', ''y'' ∈ ''S'' に対し''x'' ≤ ''y'' ⇔ ''f'' (''x'') ≤ ''f'' (''y'') である事を言う。 |
|||
* ''f''が'''{{仮リンク|順序同型|en|order isomorphism|label=順序同型写像}}'''であるとは、''f'' が順序埋め込みな全単射である事を言う。 |
|||
''f'': ''S'' → ''T'' が順序埋め込みであるとき、''S'' は''f'' によって ''T'' に(順序集合として)'''埋め込まれる'''という。 |
|||
また''f'': ''S'' → ''T'' が順序同型なとき、''S'' と''T'' は'''順序同型'''あるいは単に'''同型'''であるという。 |
|||
=== 性質 === |
|||
上で述べた概念は以下の性質を満たす: |
|||
* 順序を反映する写像は単射である。実際''f'' (''x'') = ''f'' (''y'') ⇒''f'' (''x'') ≤ ''f'' (''y'') かつ ''f'' (''x'') ≥ ''f'' (''y'') ⇒ ''x'' ≤ ''y'' かつ ''x'' ≥ ''y'' ⇒''x'' = ''y'' である。 |
|||
* ''f'' が順序埋め込みである必要十分条件は''f'' が順序を保存し、しかも順序を反映する事である。また''f'': ''S'' → ''T'' とその逆関数 ''f'' <sup>-1</sup>: ''T'' → ''S'' が順序同型なら''f'' 、''f'' <sup>-1</sup>は順序同型である。 |
|||
* 順序を保つ写像と順序を保つ写像の合成は順序を保つ。 順序を反映する写像と順序を反映する写像の合成も順序を反映する。 |
|||
===具体例=== |
|||
{| |
|||
|[[File:Monotonic but nonhomomorphic map between lattices.gif|thumb|right|x150px|順序を保つが順序を反映しない写像 (''f''(''u'')≤''f''(''v'') だが ''u''≤''v'' でない)]] |
|||
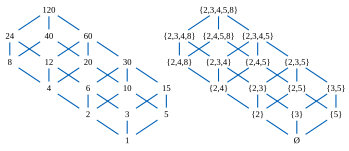
|[[File:Birkhoff120.svg|thumb|right|x150px| 120 の約数全体の成す半順序集合(整除関係で順序を入れる)と {2,3,4,5,8} の整除関係で閉じた部分集合族(包含関係で順序を入れる)との間の順序同型]] |
|||
|} |
|||
自然数全体が整除関係に関して成す半順序集合から、その[[冪集合]]が包含関係に関して成す半順序集合への写像 ''f'': ℕ → ℙ(ℕ) を各自然数にその[[素因数]]全体の成す集合を対応させることにより定まる。これは順序を保つ集合である(すなわち、''x'' が ''y'' を割るならば ''x'' の各素因数は ''y'' の素因数にもなる)が単射ではない(例えば 12 も 6 もこの写像で {2,3} に写る)し、順序を反映もしない(例えば 12 は 6 を割らない)。少し設定を変えて、各自然数にその{{仮リンク|素冪|en|prime power|label=素冪因子}}の集合を対応させる写像 ''g'': ℕ → ℙ(ℕ) を考えれば、これは順序を保ち、かつ順序を反映するから、従って順序埋め込みになる。一方、これは順序同型ではない(実際、たとえば単元集合 {4} に写る数は無い)が[[終域]]を ''g'' の[[値域]] ''g''(ℕ) に変更すれば順序同型にすることができる。このような冪集合の中への順序同型の構成は、より広汎な{{仮リンク|分配束|en|distributive lattice}}と呼ばれる半順序集合のクラスに対して一般化することができる({{仮リンク|バーコフの表現定理|en|Birkhoff's representation theorem}}の項を参照)。 |
|||
== 区間 == |
== 区間 == |
||
''P'' を順序集合とし、''a''、''b'' を''P'' の元とする時、'''[[閉区間]]''' [''a'', ''b''] と'''[[開区間]]''' (''a'', ''b'')を以下のように定義する: |
|||
: <math>[a,b]:=\{x\in P\mid a\le x\le b\}</math> |
: <math>[a,b]:=\{x\in P\mid a\le x\le b\}</math> |
||
のことをいう。これは少なくともふたつの元 ''a'' および ''b'' を含む。これに対して、"≤" に対応する狭義の順序関係 "<" を用いれば、'''[[開区間]]''' (''a'', ''b'') が ''a'' < ''x'' かつ ''x'' < ''b'' を満たす元 ''x'' 全体の成す集合 |
|||
: <math>(a,b):=\{x\in P\mid a < x < b\}</math> |
: <math>(a,b):=\{x\in P\mid a < x < b\}</math> |
||
さらに[''a'',''b'') および (''a'',''b''] を以下のように定義し、'''[[半開区間]]'''と呼ぶ: |
|||
しばしば、この定義に言うこれらの区間は ''a'' > ''b'' の場合には空集合を表すものとして扱うことがある。ただし、開区間 (''a'', ''b') はたとえ ''a'' < ''b'' の場合であっても空集合となりうる。 |
|||
: <math>[a,b):=\{x\in P\mid a\le x< b\}</math> |
|||
半順序集合が[[局所有限半順序集合|局所有限]]であるとは、すべての区間が有限集合であることを言う。たとえば、[[整数]]全体の成す集合は通常の大小関係による半順序に関して局所有限である(端点の無い無限区間のようなものは今考えていない)。 |
|||
: <math>(a,b]:=\{x\in P\mid a < x \le b\}</math> |
|||
文献によっては(''a'', ''b'')、[''a'',''b'')、 (''a'',''b''] の事を |
|||
順序集合における区間の概念と、[[区間順序]] {{lang|en|(interval order)}} として知られる特定の半順序の類とを混同してはならない。 |
|||
]''a'', ''b''[、[''a'',''b''[、 ]''a'',''b''] と表す場合もある。 |
|||
半順序集合が{{仮リンク|局所有限半順序集合|label=局所有限|en|Locally finite poset}}であるとは、すべての区間が有限集合であることを言う。たとえば、[[整数]]全体の成す集合は通常の大小関係による半順序に関して局所有限である(端点の無い無限区間のようなものは今考えていない)。 |
|||
順序集合における区間の概念と、{{仮リンク|区間順序|en|interval order}}として知られる特定の半順序の類いとを混同してはならない。 |
|||
== 順序構造と位相構造 == |
== 順序構造と位相構造 == |
||
===全順序集合の位相=== |
|||
全順序集合には次のようにして自然に[[位相空間|位相構造]]が定められる。これを'''順序位相''' (order topology) という。例えば、通常の大小関係 ≤ によって実数全体の集合 '''R''' を全順序集合と見ると、その順序位相は通常の[[距離空間|距離]]により定められる位相と同等になる。 |
|||
====順序位相==== |
|||
全順序集合''A'' に対し、無限半開区間 |
|||
: <math>(-\infty,b)=\{x \in A \mid x< b\}</math> |
|||
(''A'', ≤) を一般の全順序集合とする。無限半開区間(-∞, b)および(a, +∞)全体を[[位相空間#開基と準開基|準開基]]とする位相が定まる。これを ''A'' の順序位相という。 |
|||
: <math>(a,\infty)=\{x \in A \mid a< x\}</math> |
|||
全体の集合を[[位相空間#開基と準開基|準開基]]とする位相を'''順序位相'''([[:en:order topology|order topology]])という<ref>原理的には半順序集合であっても同様の概念を定義できるが、本稿の英語版をはじめ、筆者が調べた範囲では全順序集合に対してのみorder topologyを定義している為、ここでは全順序のみに話を限定した。</ref>。例えば、通常の大小関係 ≤ によって実数全体の集合<math>\mathbb{R}</math>を全順序集合と見ると、その順序位相は通常の[[距離空間|距離]]により定められる位相と同等になる。 |
|||
''P'' が半順序集合で[[位相空間]]の構造をも持つとき、慣習的に {(''a'', ''b'') ∈ ''P'' × ''P'' | ''a'' ≤ ''b'' } が[[直積位相]]に関する[[閉部分集合]]であるものと仮定する。この仮定の下で、半順序関係は |
|||
: <math>[(a_i\to a) \and (a_i \le b \text{ for all }i)] \Rarr a\le b</math> |
|||
全順序集合''A''の部分集合''B'' には、''B'' を全順序集合とみなした時の順序位相と ''A'' の順序位相から誘導される位相との2つの位相が入る。しかしこの'''2つの位相は一致するとは限らない'''。(''B''の順序位相における開集合は誘導位相でも開集合であるが逆は一般には成り立たない)。 |
|||
が成り立つという意味で[[数列の極限]]に関してよく振舞う {{lang|en|(well-behaved)}}({{harvtxt|Deshpande|1968}} を参照)。 |
|||
例えば''A'' を実数全体の集合とし、''A'' の部分集合 |
|||
: <math>B=\{x\mid 0<x<1\}\cup \{2\}</math> |
|||
を考えると、''A'' から''B'' に誘導される位相では一元集合{{math| {2} }} は明らかに開集合であるが、''B'' は順序集合としてみたときはそうではない。実際''B'' は(2を1に移す写像により)<math>C=\{x\mid 0<x\le 1\}</math>と順序同型だが、''C'' の順序位相で{{math| {1} }} は開集合ではないので''B'' の順序位相で{{math| {2} }} は開集合ではない。 |
|||
====上極限位相、下極限位相==== |
|||
単に「実数体上の位相」といった場合、前述の順序位相を指すがその他の位相を考える事も(主に反例として用いる為に)できる。 |
|||
実数体<math>\mathbb{R}</math>上の'''上極限位相'''とは |
|||
: <math>(a,b] = \{x\in\mathbb{R}~:~a<x \le b \}</math> |
|||
全体の集合を[[位相空間#開基と準開基|開基]]とする位相の事であり、同様に<math>\mathbb{R}</math>上の'''{{仮リンク|下極限位相|en|lower limit topology}}'''とは逆向きの半開区間 |
|||
: <math>[a,b) = \{x\in\mathbb{R}~:~a \le x < b \}</math> |
|||
全体の集合を[[位相空間#開基と準開基|開基]]とする位相の事である<ref>実数体でなくとも上極限位相と下極限位相を考える事ができるが、これも実数体以外に対してこれらの位相を定義した文献が見つけられなかったので、ここでは実数体のみを対象にした。</ref>。 |
|||
実数体に下限位相を入れた空間はしばし<math>\mathbb{R}_{\ell}</math>と書かれ、'''ゾルゲンフライ直線'''と呼ばれる。またゾルゲンフライ直線2つの直積<math>\mathbb{R}_{\ell}\times\mathbb{R}_{\ell}</math>は'''{{仮リンク|ゾルゲンフライ平面|en|Sorgenfrey plane}}'''と呼ばれる。 |
|||
====overlapping interval topology==== |
|||
区間[-1,1]上の'''[[:en:overlapping interval topology|overlapping interval topology]]'''とは |
|||
: <math>[-1,a)</math> for <math>0<a</math> |
|||
: <math>(b,1]</math> for <math>b<0</math> |
|||
を準開基とする位相である。 |
|||
===半順序集合の位相=== |
|||
====半順序空間==== |
|||
位相構造を持つ半順序集合''P'' で以下の性質を満たすものを'''{{仮リンク|半順序空間|en|partially ordered space}}'''という: |
|||
: {{math|''a'' < ''b'' }}を満たす任意の{{math|''a'', ''b'' ∈ ''P'' }}に対し、''a'' の開近傍''U''で上方集合であるものと''b'' の開近傍''V'' で下方集合であるものが存在する事である。 |
|||
(''P'' の位相構造でこの性質を満たすものは1つとは限らないが、それらを全て半順序空間という。) |
|||
なお、半順序空間と名前の似た{{仮リンク|poset topology|en|poset topology}}は別概念であるので注意が必要である。 |
|||
定義より明らかに半順序空間は常に[[ハウスドルフ空間|ハウスドルフ性]]を満たす。 |
|||
半順序空間では以下が成立する: |
|||
:{{math|''a''<sub>''i''</sub> → ''a'', ''b''<sub>''i''</sub> → ''b''}} かつ任意の ''i'' に対して {{math|''a''<sub>''i''</sub> ≤ ''b''<sub>''i''</sub>}} ならば {{math|''a'' ≤ ''b''}} である<ref name="ward-1954">{{Cite journal|first=L. E. Jr|last=Ward|title=Partially Ordered Topological Spaces|journal=Proceedings of the American Mathematical Society|volume=5 |year=1954|pages= 144–161|issue= 1|doi=10.1090/S0002-9939-1954-0063016-5}}</ref> |
|||
位相構造を持つ半順序集合''P'' が半順序空間である必要十分条件は以下を満たす事である: |
|||
: 半順序集合''P'' 上の位相構造として、{(''a'', ''b'') ∈ ''P'' × ''P'' | ''a'' ≤ ''b'' } が[[直積位相]]に関する[[閉集合|閉部分集合]]になる。 |
|||
2つ半順序空間の間の順序を保つ連続写像の事を'''dimap'''という。 |
|||
====上方位相、下方位相==== |
|||
順序集合''P'' 上の以下の2つの位相は同一である事が簡単に示せる。以下のいずれか一方(したがって両方)の条件を満たす位相を'''{{仮リンク|上方位相|en|upper topology}}'''という。 |
|||
# {''x'' ∈ ''P'' | x ≥ a} for {{math|''a'' ∈ ''P'' }}を全て閉集合とする最弱の位相 |
|||
# 任意の{{math|''a'' ∈ ''P'' }}に対し、一点集合{{math|{''a''} }}の閉包が{''x'' ∈ ''P'' | x ≥ a}と一致する最弱の位相 |
|||
'''下方位相'''も同様にして定義できる。 |
|||
====アレクサンドロフ空間==== |
|||
位相空間''P'' が'''{{仮リンク|アレクサンドロフ空間|en|Alexandroff space}}'''であるとは、''P''上の(有限または無限個の)任意の開集合の共通部分が必ず開集合になる事を言う。 |
|||
アレクサンドロフ空間は前順序集合と自然に1対1対応している事が知られている。 |
|||
実際任意の前順序集合''P'' に対し、 |
|||
: ''U'' が''P'' の開集合 ⇔ ''U'' が''P'' の上方集合 |
|||
により''P'' に位相を入れたものはアレクサンドロフ空間になる。(この位相を''P'' の'''アレクサンドロフ位相'''という。) |
|||
逆に任意のアレクサンドロフ空間''P'' に対し''P'' 上の「{{仮リンク|specialization preorder|en|specialization preorder}}」を前順序とする事で''P'' を前順序集合とみなす事ができる。 |
|||
ここで位相空間''P'' の'''specialization preorder'''とは |
|||
: <math>x \le y \iff \overline{\{x\}} \subset \overline{\{y\}}</math> |
|||
で定義される前順序の事である。上式で<math>\overline{\{x\}}</math>は一元集合{{math| {''x'' } }}の[[閉包 (位相空間論)|閉包]]である。(なお、''P''が[[コルモゴロフ空間|T<sub>0</sub>空間]]であればspecialization preorderは半順序である事が知られている。) |
|||
以上の対応関係により、集合''P'' におけるアレクサンドロフ空間としての構造と''P'' 上の前順序は1対1対応する。 |
|||
specialization preorderはアレクサンドロフ空間でなくとも定義可能であるが、アレクサンドロフ空間でない位相空間上ではspecialization preorderに対して上方集合でない開集合も存在する。(なおこの場合でも開集合は常に上方集合である)。したがって前述したような、上方集合を開集合とする位相を考えても元の位相は復元できない。 |
|||
=====実数体における例===== |
|||
実数体(に通常の順序をいれたもの)を前順序集合とみなす事で実数体にアレクサンドロフ位相を入れる事ができる。アレクサンドロフ位相における実数体上の開集合(すなわち上方集合)は以下のもののいずれかになる: |
|||
* <math>(a,\infty)</math> for some ''a'' |
|||
* <math>[a, \infty)</math> for some ''a'' |
|||
* 空集合<math>\emptyset</math>、全体集合<math>\mathbb{R}</math> |
|||
====スコット位相==== |
|||
上で述べたようにアレクサンドロフ位相は<math>[a, \infty)</math>のような「下に閉じた」集合すらも開集合とみなしてしまう。アレクサンドロフ位相からこのような不自然さを取り除いたのがスコット位相である。 |
|||
順序集合''P'' 上の'''スコット位相'''([[:en:Scott topology<!-- リダイレクト先の「[[:en:Scott continuity]]」は、[[:ja:スコット連続]] とリンク -->|Scott topology]])とは、以下の2条件を満たす''P'' の部分集合''O'' 全体の集合を開集合族とする位相である: |
|||
# ''O'' ⊂ ''P'' は上方集合である |
|||
# ''P'' の[[有向集合|有向部分集合]] ''A'' で(''A'' を自然に[[有向点族]]とみなしたときの)''A'' の極限が''O'' に入っていれば、''A'' の点で''O'' に含まれるものが存在する |
|||
後者の条件は内点概念の点列による特徴づけ(''O'' の内点''x'' に収束する点列は''O'' と共通部分を持つ)に類似しているおり、この条件が「下に閉じた」集合を排除する。 |
|||
よって実数体にスコット位相を入れた際、実数体上の開集合は以下のもののいずれかになる: |
|||
* <math>(a,\infty)</math> for some ''a'' |
|||
* 空集合<math>\emptyset</math>、全体集合<math>\mathbb{R}</math> |
|||
スコット位相を入れた順序集合を'''スコット空間'''といい、スコット空間からスコット空間への連続写像を'''[[スコット連続]]'''([[:en:Scott continuity|Scott continuity]])という。順序集合''P'' から順序集合''Q'' への写像''f'' がスコット連続である必要十分条件は以下の性質が成り立つ事である事が知られている: |
|||
* ''P'' の任意の有向部分集合''A'' に対し、''A'' が''P'' 内の上限を持てば''f'' (''A'' )も''Q'' 内の上限を持ち、sup ''f'' (''A'') = ''f'' (sup ''A'' )が成立する。 |
|||
スコット連続な関数は順序を保つ。実際、''x'' ≥ ''y'' ⇒ sup{''x'' , ''y'' } = ''x'' であるので、上述した条件より{{math|sup{''f'' (''x'' ), ''f'' (''y'' )}}}が存在し、しかもsup{''f'' (''x'' ), ''f'' (''y'' )} = ''f'' (sup{''x'' , ''y'' }) = ''f'' (''x'' )となる。これは{{math|''f'' (''x'' ) ≥ ''f'' (''y'' )}}を意味する。 |
|||
なお、スコット位相と下方位相のいずれよりも強い位相構造の中で最弱のものを'''{{仮リンク|ローソン位相|en|Lawson topology}}'''という。 |
|||
===ストーン双対性=== |
|||
位相空間の開集合全体の集合は包含関係により順序集合とみなせる。位相空間が「sober性」という弱い性質を満たす時はこの順序構造のみで位相空間の構造が特徴づけられる事が知られている([[ストーン双対性|ストーンの双対性定理]])。 |
|||
したがってsober性を満たす空間に話を限定すれば、点集合論に頼らなくても順序構造のみで位相空間論を展開できる([[ストーン双対性|ポイントレス位相空間論]])。 |
|||
== 直積集合上の順序 == |
|||
ふたつの半順序集合(の台集合)の[[直積集合]]上の半順序としては次の三種類が考えられる。 |
|||
* [[辞書式順序]]: <math>(a, b) \le (c, d) \iff a < c \or (a = c \and b \le d)</math> |
|||
* [[積順序]]: <math>(a, b) \le (c, d) \iff a \le c \and b \le d</math> |
|||
* <math>(a, b) \le (c, d) \iff (a < c \and b < d) \or (a = c \and b = d)</math> |
|||
最後の順序は対応する狭義全順序の[[関係の直積|直積]]の反射閉包である。これらの三種類の順序はいずれもふたつよりも多くの半順序集合の直積に対しても同様に定義される。 |
|||
[[体 (数学)|体]]上の[[順序線型空間]]に対してこれらの構成を適用すれば、結果として得られる順序集合はいずれもふたたび順序線型空間となる。 |
|||
<gallery> |
|||
File:Strict product order on pairs of natural numbers.svg| ℕ×ℕ 上の直積狭義順序の反射閉包。 |
|||
File:N-Quadrat, gedreht.svg| ℕ×ℕ 上の積順序 |
|||
File:Lexicographic order on pairs of natural numbers.svg| ℕ×ℕ 上の辞書式順序 |
|||
</gallery> |
|||
== 圏としての順序集合 == |
== 圏としての順序集合 == |
||
任意の半順序集合(および前順序集合)は、任意の射集合が高々一つの元からなる[[圏 (数学)|圏]]と看做すことができる。具体的には、射の集合を ''x'' ≤ ''y'' ならば hom(''x'', ''y'') = {(''x'', ''y'')} (それ以外の場合は空集合) とし、(''y'', ''z'')∘(''x'', ''y'') = (''x'', ''z'') と定義する。二つの半順序集合が[[圏同値|圏として同値]]となるのは、それらが順序集合として同型であるときであり、かつその時に限る。半順序集合に最小元が存在すればそれは[[始対象]]であり、最大元が存在すればそれは[[終対象]]となる。また、任意の前順序集合はある半順序集合に圏同値であり、半順序集合の任意の部分圏は{{仮リンク|同型射閉圏|label=同型射について閉じて|en|isomorphism-closed}}いる。 |
|||
任意の半順序集合(および[[前順序集合]])は、任意の射の集合が唯一つの元からなる[[圏 (数学)|圏]]と看做すことができる。詳しく述べれば、射の集合を |
|||
: <math>\text{hom}(x, y) = \begin{cases} |
|||
{(x, y)} & (x \le y)\\ |
|||
\emptyset & (\text{otherwise}) |
|||
\end{cases}</math> |
|||
とし、射の合成を |
|||
: <math>(y, z)\circ(x, y) = (x, z)</math> |
|||
で定めるのである。ふたつの半順序集合が[[同値関係|同値]]であるというのを、それらが同型であることとして定める。半順序集合を圏と見たとき、半順序集合における最小元はいずれも[[始対象]]であり、最大元はいずれも[[終対象]]である。また、任意の前順序集合はある半順序集合に同値であり、半順序集合の任意の部分圏は[[同型射閉圏|同型射について閉じて]]いる。 |
|||
半順序集合からの函手、すなわち半順序圏で添字付けられた[[図式 (圏論)|図式]]は、[[可換図式]]である。 |
半順序集合からの函手、すなわち半順序圏で添字付けられた[[図式 (圏論)|図式]]は、[[可換図式]]である。 |
||
== その他 == |
|||
* ('''半順序関係の総数''')<!-- [[Image:poset6.jpg|right|thumb|250px| Partially ordered set of [[power set|set of all subsets]] of a six-element set {a, b, c, d, e, f}, ordered by the subset relation.]]-->''n'' 個の元からなる集合上の半順序の総数(狭義半順序の総数も同じ)は {{OEIS|A001035}} <!-- {{Number of relations}} -->[[違いを除いて|同型を除いた]]総数は 1, 1, 2, 5, 16, 63, 318, … {{OEIS|A000112}}. |
|||
* ('''線型順序拡大''')半順序集合''P'' の全順序集合への埋め込みを'''線形順序拡大'''([[:en:linear extension|linear extension]])という。任意の半順序は全順序に拡張することができる({{仮リンク|順序拡大原理|en|order-extension principle}}<ref>{{cite book |last=Jech |first=Thomas |title=The Axiom of Choice |year=2008 |origyear=originally published in 1973 |publisher=[[Dover Publications]] |isbn=0-486-46624-8}}</ref>)。[[計算機科学]]において([[有向非循環グラフ]]の{{仮リンク|到達可能性|en|reachability}}順序として表現される)半順序の線型拡張を求めるアルゴリズムは[[位相ソート]] {{lang|en|(topological sorting)}} と呼ばれる。 |
|||
== 関連項目 == |
|||
{{colbegin|3}} |
|||
* {{仮リンク|反マトロイド|en|antimatroid}}: 半順序集合よりも一般の順序付けの族を許すような、集合上の順序付けの一般化 |
|||
* [[因果集合]] |
|||
* {{仮リンク|比較可能グラフ|en|comparability graph}} |
|||
* [[有向集合]] |
|||
* {{仮リンク|次数付き順序集合|en|graded poset}} |
|||
* [[半束]] |
|||
* [[束 (順序集合論)]] |
|||
* [[順序群]] |
|||
* {{仮リンク|準順序|en|semiorder}} (semiorder) |
|||
* {{仮リンク|直並列半順序|en|series-parallel partial order}} |
|||
* {{仮リンク|狭義弱順序|en|strict weak ordering}}: "''a'' < ''b'' または ''b'' < ''a'' の何れかが成り立つ" という関係が推移的となるような狭義半順序 "<" |
|||
* [[完備半順序]] (cpo) |
|||
* [[ツォルンの補題]] |
|||
{{colend}} |
|||
== 注記 == |
== 注記 == |
||
| 173行目: | 368行目: | ||
== 参考文献 == |
== 参考文献 == |
||
* Jayant V. Deshpande |
* {{Cite journal|first=Jayant V. |last=Deshpande|title= On Continuity of a Partial Order|journal= Proceedings of the American Mathematical Society|volume= 19|year= 1968|pages= 383–386|issue= 2|doi=10.1090/S0002-9939-1968-0236071-7|postscript=.}} |
||
* Bernd S. W. Schröder |
* {{cite book|first=Bernd S. W. |last=Schröder|title= Ordered Sets: An Introduction |publisher=Birkhäuser, Boston|year=2003}} |
||
* |
* {{cite book|first=Richard P.|last=Stanley|authorlink=Richard P. Stanley|title=Enumerative Combinatorics 1|series=Cambridge Studies in Advanced Mathematics|volume=49|publisher=Cambridge University Press|isbn=0-521-66351-2}} |
||
== 外部リンク == |
== 外部リンク == |
||
{{Commons|Hasse diagram|Hasse diagram}} |
|||
* ''n'' 個の元に入れられる半順序関係の個数を示した数列 [{{fullurl:OEIS:A001035}} A001035] : [[オンライン整数列大辞典|OEIS]] |
|||
* {{OEIS|A001035}}: Number of posets with ''n'' labeled elements in the [[On-Line Encyclopedia of Integer Sequences|OEIS]] |
|||
* {{OEIS|A000112}}: Number of posets with ''n'' unlabeled elements in the OEIS |
|||
== 関連項目 == |
|||
* [[順序数]] |
|||
* [[順序型]] |
|||
* [[単項式順序]] |
|||
* [[ソート]] |
|||
* [[ハッセ図]] |
|||
{{DEFAULTSORT:しゆんしよしゆうこう}} |
{{DEFAULTSORT:しゆんしよしゆうこう}} |
||
[[Category:順序構造|*]] |
[[Category:順序構造|*]] |
||
[[Category:数学に関する記事]] |
[[Category:数学に関する記事]] |
||
[[be:Дачыненне парадку]] |
|||
[[fa:مجموعه جزئا مرتب]] |
|||
2015年4月27日 (月) 13:07時点における版
数学において順序集合(じゅんじょしゅうごう、英: ordered set)とは 「順序」の概念が定義された集合の事で、「順序」とは大小、高低、長短等の序列に関わる概念を抽象化したものである。
ただし順序集合内の2つの元a、b に順序関係が定まっている必要はなく、両者が「比較不能」であってもよい。よってa、b の関係は「a はb 以上である」、「b はa 以上である」、「a とb は比較不能である」の3通りのいずれかとなる。
比較不能のケースを許容している強調して順序集合の事を半順序集合(はんじゅんじょしゅうごう、英: partially ordered set, poset)ともいう。一方、半順序集合の中で特に比較不能のケースがないものをしないものを全順序集合(totally ordered set)という。(「半順序」という言葉が「全順序」の対義語ではない事に注意。全順序集合も半順序集合の一種である)。
全順序集合の簡単な例は整数の集合や実数の集合で、通常の大小比較を順序とみなしたものがある。
一方、全順序ではない半順序集合の例としては(2つ以上元を含む)集合の冪集合で、包含関係を順序とみなしたものがある。例えば3元集合P ={a,b,c}において{a,b}と{b,c}はいずれも他方を包含していないのでP の冪集合は全順序ではない。実生活に近い例では、「AさんはBさんの子孫である」という事を「A<B」という大小関係とみなす事で人間全体の集合を半順序集合とみなせる。AさんとBさんはどちらも他方の子孫でない事もありうる(兄弟同士、叔父と甥、赤の他人等)ので、この順序集合は全順序ではない。
定義
全順序集合、半順序集合、およびこれらよりさらに弱い概念である前順序集合の定義を述べる為にまず以下の性質を考える。ここでP は集合であり、「≤」をP 上で定義された二項関係 である。
「≤」が全順序律を満たさない場合、「a ≤ b」でも「b ≤ a」でもないケースがある。このような第三のケースにあるときa とbは比較不能であるという。
前順序・半順序・全順序
P を集合とし、≤ を P 上で定義された二項関係 とする。
- ≤ が反射律と推移律を満たすとき ≤ を P 上の前順序という。
- 前順序な ≤ が反対称律をも満たすとき ≤ を P 上の半順序という。
- 半順序な ≤ が全順序律をも満たすとき ≤ を P 上の全順序という。
≤ が前順序である (P, ≤) を前順序集合という。同様に ≤ が半順序なら (P, ≤) は半順序集合、全順序なら (P, ≤) は全順序集合である。また集合 P は (P, ≤) の台 (support) と呼ばれる。紛れがなければ ≤ を省略し、P の事を(いずれかの意味で)順序集合という。
順序集合 (P, ≤) に対し、≤ を台 P 上の順序関係ともいう。 なお多くの数学の分野では半順序集合を主に扱うので、単に順序あるいは順序集合といった場合はそれぞれ半順序、半順序集合を意味する場合が多いが、分野によっては、主な対象が半順序集合でなく前順序集合や全順序集合である場合があり、そのような分野では前順序集合や全順序集合の意味で「順序集合」という言葉が用いられることがあるので注意が必要である。
上では順序を記号 ≤ で表したが、必ずしもこの記号で表現する必要はない。 実数の大小を表す記号 ≤ と区別する為、順序の記号として や を使うこともある。
全順序の事を線型順序ともいい、全順序集合のことを鎖と呼ぶこともある。また半順序集合の部分集合 A で A の任意の相異なる二元が比較不能であるものを反鎖という。
半順序集合の元 a が他の元 b によって被覆される a <: b とは、a は b よりも真に小さく、かつそれらの間に別の元が入ることはないこと(後述する狭義の記号を使って書けば a < b かつ任意の c に対して a < c < b が偽となること)をいう。
順序集合の例
- 自然数全体の集合 N、整数全体の集合 Z、有理数全体の集合 Q、実数全体の集合 R は通常の代数的な大小関係によって全順序集合になるが、複素数はそうではない。複素数全体の集合 C に R × R としての辞書式順序を定めたものは全順序集合であるが、この順序は複素数の乗法とは両立しない。
- 自然数全体の成す集合は整除関係を順序として半順序集合である。
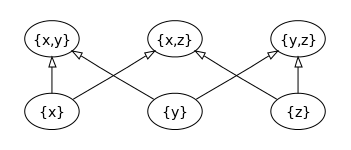
- ある集合の冪集合は部分集合の包含関係を順序として半順序集合となる。これは一般には全順序ではない。例えば {1, 2, 3} の冪集合について、たとえば {1, 2} と {2, 3} を考えれば、これらは比較不能である({1, 2} ≤ {2, 3} でも {2, 3} ≤ {1, 2} でもない)。
- ベクトル空間の部分空間全体は包含関係で順序付けられた半順序集合である。
- 半順序集合 P に対し、P の元の列全体の成す集合は、列 a, b に対し、と定めると半順序集合となる。
- 集合 X と半順序集合 P に対し、X から P への写像全体の成す写像空間は、ふたつの写像 f, g に対して、f ≤ g を X の任意の元 x に対して f(x) ≤ g(x) となることとして定義すると、半順序集合になる。
- 非循環有向グラフの頂点集合は、到達不可能性によって順序付けられる。
- 半順序集合における順序関係の向きが a < b > c < d ... というように交互に入れ替わる列をフェンスと呼ぶ。
逆順序、狭義の順序、双対順序
上で述べた順序関係「≤」は直観的には左辺が右辺よりも「小さい、もしくは等しい」事を意味しているが、逆に左辺が右辺よりも「大きい、もしくは等しい」順序関係や等しい事を許容しない順序関係を考える事もできる。
逆順序
「大きい、もしくは等しい」事を意味する順序関係は「≤」の逆順序と呼ばれ、
により定義される。
狭義の順序
一方、等しい事を許容しない順序は狭義の(半)順序と呼ばれ、以下のように定義される:
- ...(1)
狭義の逆順序「>」も自然に定義される。
狭義の順序「<」の対義語として、等しい事も許容する順序「≤」の事を広義の(半)順序(もしくは弱い意味 (weak) の(半)順序、反射的 (reflexive) な(半)順序)という。
(1)式で定義された「<」を「≤」の反射的簡約 (reflexive reduction) という。
「≤」が半順序であるとき、その反射的簡約「<」は任意のa, b, c ∈ P に対して以下を満たす:
- 非反射性
- ¬(a < a);
- 非対称性
- a < b ならば ¬(b < a);
- 推移性
- a < b かつ b < c ならば a < c
以上では広義の順序からスタートして狭義の順序を定義したが、逆に上の三性質を満たすものを狭義の順序として定義し、広義の順序を
- ...(2)
により定義する事もできる。 この場合、(2)式で定義された「≤」を「<」の反射閉包という。 「<」が前述の3条件を満たせば反射閉包「≤」が半順序である事を簡単に示す事ができる。
双対順序集合
(P , ≤)を順序集合とするとき、P 上の二項関係「」を
と定義する(すなわち「」は「≤」の逆順序を順序とみなしたものである)。すると、「」もP 上の順序になっている事が簡単に示せる。を(P , ≤)の双対順序集合という。
双対順序集合はその定義よりもとの順序集合(P , ≤)とは大小が逆転している。したがって(P , ≤)における上限、極大元、最大元はではそれぞれ下限、極小元、最小元になる。
ハッセ図
P を有限集合とし、「<」をP 上の狭義の半順序とするとき、以下のようにしてP を自然に単純有向グラフとみなせる:
- 頂点:Pの元
- a ∈ P から b ∈ P への辺がある⇔ a < b であり、しかもa < c < bを満たすc ∈ Pが存在しない。(すなわちb はa を被覆している)。
この有向グラフを図示したものをハッセ図という。
右に示した図がハッセ図の例である。この図では三元集合 {x, y, z}の 部分集合の全体を包含関係を順序とする順序集合とみなしたものをハッセ図として表している。
ハッセ図を用いると、順序関係に関する基本的な概念が図示できる。 例えばこの図で {x} と {x,y,z} は比較可能だが、{x} と {y} は比較不能である。 また一元集合の族 {{x}, {y}, {z}}は反鎖である。 さらに{x} は {x,z} によって被覆されるが、{x,y,z} には被覆されない。
なお、有限半順序集合から前述の方法で作ったグラフは閉路を持たない。 逆に(V , E )を閉路を持たない有限な単純有向グラフとすると、V 上に以下の順序を入れる事でV を半順序集合とみなせる:
- a < b ⇔ a からb への道がある
したがって有限半順序集合は閉路を持たない有限な単純有向グラフと自然に同一視できる。
上界、最大、極大、上限、上方集合
P を半順序集合とし、A をその部分集合とし、x を P の元とする。 このとき上界、最大、極大、上限の概念、およびこれらの双対概念である下界、最小、極小、下限は以下のように定義される:
定義
- x が A の上界(resp. 下界): ∀y ∈ A : y ≤ x (resp. y ≥ x)
- x が A の最大元(resp. 最小元): x は A の元でしかも x は A の上界(resp. 下界)である
- x が A の極大元(resp. 極小元): x は A の元でしかも (resp. ) を満たす y ∈ A が存在しない
- x が A の上限(resp. 下限): x は集合{y ∈ P | y は A の上界(resp. 下界)} の最小元(resp. 最大元)
上界および上限の定義において x が A に必ずしも属さないことには注意が必要である。
極大元の概念と最大元の概念は以下の点で異なる。 まず x が A の極大元であるとは、A の元は「x 以下である」か、もしくは「x とは大小が比較不能である」かのいずれかである事を意味する。一方 x が A の最大元であるとは A の元は常に x 以下である事を意味する(このとき A の元は x と比較可能である)。したがって最大元は極大元であるが、極大元は必ずしも最大元であるとは限らない。
さらに A が P の上方集合(resp. 下方集合)であるとは、任意の a ∈ A と x > a (resp. x < a) を満たす任意の P の元に対しx ∈ A となることをいう。
具体例
 |
 |
正整数全体の成す集合を整除関係で順序付ける時、1 は任意の正整数を割り切るという意味において 1 は最小元である。しかしこの半順序集合には最大元は存在しない(任意の正整数の倍数としての 0 を追加して考えたとするならば、それが最大元になる)。この半順序集合には極大元も存在しない。実際、任意の元 g はそれとは異なる例えば 2g を割り切るから g は極大ではありえない。この半順序集合から最小元である 1 を除いて、順序はそのまま整除関係によって入れるならば、最小元は無くなるが、極小元として任意の素数をとることができる。この半順序に関して 60 は部分集合 {2,3,5,10} の上界(上限ではない)を与えるが、1 は除かれているので下界は持たない。他方、2 の冪全体の成す部分集合に対して 2 はその下界(これは下限でもある)を与えるが、上界は存在しない。
写像と順序
順序に関する写像の概念に以下のものがある:
定義
S 、T を順序集合とし、f: S → T を写像とする。このとき
- f: S → T が順序を保つ(order-preserving。同調 (isotone)とも) とは、任意の x, y ∈ S に対して x ≤ y ⇒ f (x) ≤ f (y) である事を言う。
- f: S → T が順序を逆にする(order-reversing)とは、任意の x, y ∈ S に対して x ≤ y ⇒ f (x) ≥ f (y) である事を言う。
- 上の2つを合わせて単調(monotone) 写像と言う。
- fが順序を反映する (order-reflecting) とは任意の x, y ∈ S に対して f (x) ≤ f (y) ⇒ x ≤ y であることを言う。
- f が順序埋め込みであるとは、任意の x, y ∈ S に対しx ≤ y ⇔ f (x) ≤ f (y) である事を言う。
- fが順序同型写像であるとは、f が順序埋め込みな全単射である事を言う。
f: S → T が順序埋め込みであるとき、S はf によって T に(順序集合として)埋め込まれるという。 またf: S → T が順序同型なとき、S とT は順序同型あるいは単に同型であるという。
性質
上で述べた概念は以下の性質を満たす:
- 順序を反映する写像は単射である。実際f (x) = f (y) ⇒f (x) ≤ f (y) かつ f (x) ≥ f (y) ⇒ x ≤ y かつ x ≥ y ⇒x = y である。
- f が順序埋め込みである必要十分条件はf が順序を保存し、しかも順序を反映する事である。またf: S → T とその逆関数 f -1: T → S が順序同型ならf 、f -1は順序同型である。
- 順序を保つ写像と順序を保つ写像の合成は順序を保つ。 順序を反映する写像と順序を反映する写像の合成も順序を反映する。
具体例
 |
 |
自然数全体が整除関係に関して成す半順序集合から、その冪集合が包含関係に関して成す半順序集合への写像 f: ℕ → ℙ(ℕ) を各自然数にその素因数全体の成す集合を対応させることにより定まる。これは順序を保つ集合である(すなわち、x が y を割るならば x の各素因数は y の素因数にもなる)が単射ではない(例えば 12 も 6 もこの写像で {2,3} に写る)し、順序を反映もしない(例えば 12 は 6 を割らない)。少し設定を変えて、各自然数にその素冪因子の集合を対応させる写像 g: ℕ → ℙ(ℕ) を考えれば、これは順序を保ち、かつ順序を反映するから、従って順序埋め込みになる。一方、これは順序同型ではない(実際、たとえば単元集合 {4} に写る数は無い)が終域を g の値域 g(ℕ) に変更すれば順序同型にすることができる。このような冪集合の中への順序同型の構成は、より広汎な分配束と呼ばれる半順序集合のクラスに対して一般化することができる(バーコフの表現定理の項を参照)。
区間
P を順序集合とし、a、b をP の元とする時、閉区間 [a, b] と開区間 (a, b)を以下のように定義する:
さらに[a,b) および (a,b] を以下のように定義し、半開区間と呼ぶ:
文献によっては(a, b)、[a,b)、 (a,b] の事を ]a, b[、[a,b[、 ]a,b] と表す場合もある。
半順序集合が局所有限であるとは、すべての区間が有限集合であることを言う。たとえば、整数全体の成す集合は通常の大小関係による半順序に関して局所有限である(端点の無い無限区間のようなものは今考えていない)。
順序集合における区間の概念と、区間順序として知られる特定の半順序の類いとを混同してはならない。
順序構造と位相構造
全順序集合の位相
順序位相
全順序集合A に対し、無限半開区間
全体の集合を準開基とする位相を順序位相(order topology)という[1]。例えば、通常の大小関係 ≤ によって実数全体の集合を全順序集合と見ると、その順序位相は通常の距離により定められる位相と同等になる。
全順序集合Aの部分集合B には、B を全順序集合とみなした時の順序位相と A の順序位相から誘導される位相との2つの位相が入る。しかしこの2つの位相は一致するとは限らない。(Bの順序位相における開集合は誘導位相でも開集合であるが逆は一般には成り立たない)。
例えばA を実数全体の集合とし、A の部分集合
を考えると、A からB に誘導される位相では一元集合 {2} は明らかに開集合であるが、B は順序集合としてみたときはそうではない。実際B は(2を1に移す写像により)と順序同型だが、C の順序位相で {1} は開集合ではないのでB の順序位相で {2} は開集合ではない。
上極限位相、下極限位相
単に「実数体上の位相」といった場合、前述の順序位相を指すがその他の位相を考える事も(主に反例として用いる為に)できる。
実数体上の上極限位相とは
全体の集合を開基とする位相の事であり、同様に上の下極限位相とは逆向きの半開区間
実数体に下限位相を入れた空間はしばしと書かれ、ゾルゲンフライ直線と呼ばれる。またゾルゲンフライ直線2つの直積はゾルゲンフライ平面と呼ばれる。
overlapping interval topology
区間[-1,1]上のoverlapping interval topologyとは
- for
- for
を準開基とする位相である。
半順序集合の位相
半順序空間
位相構造を持つ半順序集合P で以下の性質を満たすものを半順序空間という:
- a < b を満たす任意のa, b ∈ P に対し、a の開近傍Uで上方集合であるものとb の開近傍V で下方集合であるものが存在する事である。
(P の位相構造でこの性質を満たすものは1つとは限らないが、それらを全て半順序空間という。) なお、半順序空間と名前の似たposet topologyは別概念であるので注意が必要である。
定義より明らかに半順序空間は常にハウスドルフ性を満たす。
半順序空間では以下が成立する:
- ai → a, bi → b かつ任意の i に対して ai ≤ bi ならば a ≤ b である[3]
位相構造を持つ半順序集合P が半順序空間である必要十分条件は以下を満たす事である:
2つ半順序空間の間の順序を保つ連続写像の事をdimapという。
上方位相、下方位相
順序集合P 上の以下の2つの位相は同一である事が簡単に示せる。以下のいずれか一方(したがって両方)の条件を満たす位相を上方位相という。
- {x ∈ P | x ≥ a} for a ∈ P を全て閉集合とする最弱の位相
- 任意のa ∈ P に対し、一点集合{a} の閉包が{x ∈ P | x ≥ a}と一致する最弱の位相
下方位相も同様にして定義できる。
アレクサンドロフ空間
位相空間P がアレクサンドロフ空間であるとは、P上の(有限または無限個の)任意の開集合の共通部分が必ず開集合になる事を言う。
アレクサンドロフ空間は前順序集合と自然に1対1対応している事が知られている。 実際任意の前順序集合P に対し、
- U がP の開集合 ⇔ U がP の上方集合
によりP に位相を入れたものはアレクサンドロフ空間になる。(この位相をP のアレクサンドロフ位相という。)
逆に任意のアレクサンドロフ空間P に対しP 上の「specialization preorder」を前順序とする事でP を前順序集合とみなす事ができる。
ここで位相空間P のspecialization preorderとは
で定義される前順序の事である。上式では一元集合 {x } の閉包である。(なお、PがT0空間であればspecialization preorderは半順序である事が知られている。)
以上の対応関係により、集合P におけるアレクサンドロフ空間としての構造とP 上の前順序は1対1対応する。
specialization preorderはアレクサンドロフ空間でなくとも定義可能であるが、アレクサンドロフ空間でない位相空間上ではspecialization preorderに対して上方集合でない開集合も存在する。(なおこの場合でも開集合は常に上方集合である)。したがって前述したような、上方集合を開集合とする位相を考えても元の位相は復元できない。
実数体における例
実数体(に通常の順序をいれたもの)を前順序集合とみなす事で実数体にアレクサンドロフ位相を入れる事ができる。アレクサンドロフ位相における実数体上の開集合(すなわち上方集合)は以下のもののいずれかになる:
- for some a
- for some a
- 空集合、全体集合
スコット位相
上で述べたようにアレクサンドロフ位相はのような「下に閉じた」集合すらも開集合とみなしてしまう。アレクサンドロフ位相からこのような不自然さを取り除いたのがスコット位相である。 順序集合P 上のスコット位相(Scott topology)とは、以下の2条件を満たすP の部分集合O 全体の集合を開集合族とする位相である:
後者の条件は内点概念の点列による特徴づけ(O の内点x に収束する点列はO と共通部分を持つ)に類似しているおり、この条件が「下に閉じた」集合を排除する。
よって実数体にスコット位相を入れた際、実数体上の開集合は以下のもののいずれかになる:
- for some a
- 空集合、全体集合
スコット位相を入れた順序集合をスコット空間といい、スコット空間からスコット空間への連続写像をスコット連続(Scott continuity)という。順序集合P から順序集合Q への写像f がスコット連続である必要十分条件は以下の性質が成り立つ事である事が知られている:
- P の任意の有向部分集合A に対し、A がP 内の上限を持てばf (A )もQ 内の上限を持ち、sup f (A) = f (sup A )が成立する。
スコット連続な関数は順序を保つ。実際、x ≥ y ⇒ sup{x , y } = x であるので、上述した条件よりsup{f (x ), f (y )}が存在し、しかもsup{f (x ), f (y )} = f (sup{x , y }) = f (x )となる。これはf (x ) ≥ f (y )を意味する。
なお、スコット位相と下方位相のいずれよりも強い位相構造の中で最弱のものをローソン位相という。
ストーン双対性
位相空間の開集合全体の集合は包含関係により順序集合とみなせる。位相空間が「sober性」という弱い性質を満たす時はこの順序構造のみで位相空間の構造が特徴づけられる事が知られている(ストーンの双対性定理)。 したがってsober性を満たす空間に話を限定すれば、点集合論に頼らなくても順序構造のみで位相空間論を展開できる(ポイントレス位相空間論)。
直積集合上の順序
ふたつの半順序集合(の台集合)の直積集合上の半順序としては次の三種類が考えられる。
最後の順序は対応する狭義全順序の直積の反射閉包である。これらの三種類の順序はいずれもふたつよりも多くの半順序集合の直積に対しても同様に定義される。
体上の順序線型空間に対してこれらの構成を適用すれば、結果として得られる順序集合はいずれもふたたび順序線型空間となる。
-
ℕ×ℕ 上の直積狭義順序の反射閉包。
-
ℕ×ℕ 上の積順序
-
ℕ×ℕ 上の辞書式順序
圏としての順序集合
任意の半順序集合(および前順序集合)は、任意の射集合が高々一つの元からなる圏と看做すことができる。具体的には、射の集合を x ≤ y ならば hom(x, y) = {(x, y)} (それ以外の場合は空集合) とし、(y, z)∘(x, y) = (x, z) と定義する。二つの半順序集合が圏として同値となるのは、それらが順序集合として同型であるときであり、かつその時に限る。半順序集合に最小元が存在すればそれは始対象であり、最大元が存在すればそれは終対象となる。また、任意の前順序集合はある半順序集合に圏同値であり、半順序集合の任意の部分圏は同型射について閉じている。
半順序集合からの函手、すなわち半順序圏で添字付けられた図式は、可換図式である。
その他
- (半順序関係の総数)n 個の元からなる集合上の半順序の総数(狭義半順序の総数も同じ)は オンライン整数列大辞典の数列 A001035 同型を除いた総数は 1, 1, 2, 5, 16, 63, 318, … オンライン整数列大辞典の数列 A000112.
- (線型順序拡大)半順序集合P の全順序集合への埋め込みを線形順序拡大(linear extension)という。任意の半順序は全順序に拡張することができる(順序拡大原理[4])。計算機科学において(有向非循環グラフの到達可能性順序として表現される)半順序の線型拡張を求めるアルゴリズムは位相ソート (topological sorting) と呼ばれる。
関連項目
注記
- ^ 原理的には半順序集合であっても同様の概念を定義できるが、本稿の英語版をはじめ、筆者が調べた範囲では全順序集合に対してのみorder topologyを定義している為、ここでは全順序のみに話を限定した。
- ^ 実数体でなくとも上極限位相と下極限位相を考える事ができるが、これも実数体以外に対してこれらの位相を定義した文献が見つけられなかったので、ここでは実数体のみを対象にした。
- ^ Ward, L. E. Jr (1954). “Partially Ordered Topological Spaces”. Proceedings of the American Mathematical Society 5 (1): 144–161. doi:10.1090/S0002-9939-1954-0063016-5.
- ^ Jech, Thomas (2008) [originally published in 1973]. The Axiom of Choice. Dover Publications. ISBN 0-486-46624-8
参考文献
- Deshpande, Jayant V. (1968). “On Continuity of a Partial Order”. Proceedings of the American Mathematical Society 19 (2): 383–386. doi:10.1090/S0002-9939-1968-0236071-7.
- Schröder, Bernd S. W. (2003). Ordered Sets: An Introduction. Birkhäuser, Boston
- Stanley, Richard P.. Enumerative Combinatorics 1. Cambridge Studies in Advanced Mathematics. 49. Cambridge University Press. ISBN 0-521-66351-2
外部リンク
- オンライン整数列大辞典の数列 A001035: Number of posets with n labeled elements in the OEIS
- オンライン整数列大辞典の数列 A000112: Number of posets with n unlabeled elements in the OEIS

















![{\displaystyle [a,b]:=\{x\in P\mid a\leq x\leq b\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d2dcddd1d6fae7736665dfb6078521fbc4f8ff2)


![{\displaystyle (a,b]:=\{x\in P\mid a<x\leq b\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5de16036e86c1f2e042103239c7bbd375d1a2ffe)





![{\displaystyle (a,b]=\{x\in \mathbb {R} ~:~a<x\leq b\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fbb3d2204163c48af4f24a8db8cf9ed19b1b362)





![{\displaystyle (b,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cda305d993b917d73f3c1dccf001af9d8cc8faf6)