冪対象

数学の特に圏論における指数対象（しすうたいしょう、英: exponential object）は、集合論における写像空間（配置集合）に相当する、圏論における対象である。任意の有限積と指数対象を持つ圏はデカルト閉圏という。指数対象は冪対象（べきたいしょう、英: power object）や配置対象（map object; 写像対象）とも呼ばれる（が、「冪対象」という呼称は、トポス論において「冪集合」のアナロジーとして本項で言うのとは異なる意味で用いるので注意すべきである）。

定義

C は二項積を持つ圏とし、Y, Z は C の対象とする。指数対象 Z^Y は 関手 — × Y から Z への普遍射として定義することができる（この C から C への函手 — × Y は対象 X を X × Y へ写し、射 φ を φ × id_Y へ写すような函手である）。

この定義を陽に述べるならば以下のようになる。評価射

$\mathrm{eval}\colon (Z^Y \times Y) \to Z$

を伴う対象 Z^Y が指数対象であるとは、任意の対象 X と射 g: (X × Y) → Z に対し、射

$\lambda g\colon X\to Z^Y$

で次の図式

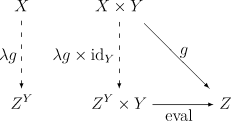
を可換とするものが一意的に存在するときに言う。C の各対象 Z に対して指数対象 Z^Y が存在するならば、Z を Z^Y へ写す函手は、函手 — × Y の右随伴となる。この場合、射集合 (hom-set) の間の自然な全単射

$\mathrm{Hom}(X\times Y,Z) \cong \mathrm{Hom}(X,Z^Y)$

が取れる。

（注意: 函数型言語では、ここで言う射 "eval" をしばしば適用 "​apply​" と呼び、構文 λg をしばしば ​curry(g)​ と書く。ここで言う射 "eval" を、何らかの言語における、引数にとった式の値を返す（式を評価する）評価函数 ​eval​ と混同してはならない）。

射 g および λg が、互いに他の「指数随伴」(exponential adjoints) と呼ばれることもある。

例

集合の圏における指数対象 Z^Y は Y から Z への写像全体の成す集合として与えられる。射 eval: (Z^Y × Y) → Z は、順序対 (f, y) を f(y) へ写す評価写像に他ならない。任意の射 g: (X × Y) → Z に対して、射 λg: X → Z^Y は g のカリー化

$\lambda g(x)(y) = g(x,y)$

によって与えられる。

位相空間の圏における指数対象 Z^Y は Y が局所コンパクトハウスドルフ空間として与えられれば存在する。この場合、空間 Z^Y はコンパクト開位相に関して連続な Y から Z への写像全体の成す集合として与えられる。評価射に関しては集合の圏のときと同様である。Y が局所コンパクトハウスドルフでないならば、指数対象は存在しない（空間 Z^Y 自体は存在するのだが、評価射が連続とは限らないために指数対象になれないのである）。このことから、位相空間の圏はデカルト閉でないことが従う。だからと言って、局所コンパクト位相空間の圏を考えたのでは、Z と Y が局所コンパクトでも空間 Z^Y は必ずしも局所コンパクトではないから、やはりデカルト閉圏にはならない。

参考文献

• Adámek, Jiří; Horst Herrlich, George Strecker (2006) [1990]. Abstract and Concrete Categories (The Joy of Cats). John Wiley & Sons. http://katmat.math.uni-bremen.de/acc/. 

外部リンク

• Interactive Web page which generates examples of exponential objects and other categorical constructions. Written by Jocelyn Paine.