平方根

平方根（へいほうこん、英語: square root）とは、ある値が与えられた時、平方してもとの値となるような新たな値のことをいう。幾何学的には、与えられた値を面積として持つ正方形を考えるとき、その一辺の長さは面積の平方根（の一つ）を与えるということで平方根のひとつの意味づけができる。また、単位長さと任意の長さ x が与えられたとき、長さ x の平方根は定規とコンパスを用いて作図することができる。二乗根（にじょうこん）、自乗根（じじょうこん）とも言う。

定義

ある与えられた値 a に対して、a = b² となるような b を一般に、a の平方根という。ただし、これらがどのような値をとるかによって、この概念が意味を持つかどうかということを含め、さまざまな点で差異が生じるということに注意が必要である。

a = 0 ならば a の平方根は 0 のみである。また、どんな正の実数 a に対しても平方根は正と負の2つ存在し、そのうち正である方を根号（こんごう、radical symbol）√ を用いて

{\sqrt {a}}

のように表して「正の（あるいは非負の）平方根」（principal square root; 主平方根）と呼ぶ（文脈上紛れのおそれの無いと思われるときは「正の」を省略してしまうこともある）。このとき、もう一方の「負の平方根」は −√a と表すことができる。また、2つの平方根を合わせて ±√a と表記することもできる。例えば、16 の平方根は 4 と −4 の2つであり、√16 は正である 4 の方を表す。√0 は、0 の唯一の平方根 0 を意味すると約束する。根号に関するこれらの規約は、非負の実数の範囲でのみ通用する便宜的なものであることに注意を要する。

負の実数に対する平方根は、考える数の範囲を複素数まで拡大してやれば定義できる。また、数とは限らず、もっと一般にいくつかの数学的対象についても、それぞれに意味のある仕方で平方根が定義されるものがある（正定値行列など）。

いくつかの基本的なこと

与えられた値 a が整数であっても、 a の平方根が整数になるとは限らない。例えば √10 は小数表示すれば 3.16227766016… と小数部分が無限に続く無理数である。平方根がふたたび整数となるような整数は平方数と呼ばれる。整数や小数で表された数の平方根を、筆算で求める方法が知られていて、それを開平法という。

0 < a, x, y について a = x²y が成り立つならば、その正の平方根について √a = x√y と書くことができるから、整数 a が平方因子を持つ場合は、根号の中身が小さい別表示が与えられる。例えば 18 = 3² × 2 であるから、√18 = 3√2 と表せる。

いくつか基本的な数の平方根については、概数として大体の値を知る必要から、以下のような無限小数の数桁目までの値を覚えるための語呂合わせが知られている。

${\sqrt {2}}=1.41421356\ldots$ 一夜一夜に人見頃（ひとよひとよにひとみごろ）
${\sqrt {3}}=1.7320508075\ldots$ 人並みに奢れや女子（ひとなみにおごれやおなご）
${\sqrt {5}}=2.2360679\ldots$ 富士山麓鸚鵡鳴く（ふじさんろくおーむなく）
${\sqrt {6}}=2.4494897\ldots$ ツヨシ串焼くな（つよしくしやくな）、煮よ良く弱く（によよくよわく） $\approx$ 2.44949 似よ良く良く（によよくよく）、二夜しくしく（によしくしく）
${\sqrt {7}}=2.64575\ldots$ 菜 (7) に虫いない（（な）にむしいない）
${\sqrt {8}}=2.828427\ldots$ ニヤニヤ呼ぶな（にやにやよぶな）
${\sqrt {10}}=3.162277\ldots$ 父 (10) さん一郎兄さん（とうさんいちろーにーさん）

実数 x に対して、その平方 x² は非負の実数であって

{\sqrt {x^{2}}}=|x|\left(={\begin{cases}x,&{\mbox{if }}x\geq 0\\-x,&{\mbox{if }}x\leq 0\end{cases}}\right)

が成り立つ。ここで |x| は x の絶対値である。また、x と y が非負の実数であるときには

{\sqrt {xy}}={\sqrt {x}}{\sqrt {y}}

が成り立つ。これは（証明を述べれば明らかであるが）非負の実数に対してその非負の平方根が一意に定まるということに依存して成立しており、後に述べるようにもっと一般の場合には保障されず実際に複素数の範囲の議論では破綻する。また、非負実数 x に対しては、その冪乗と冪根について

x=({\sqrt {x}})^{2}=({\sqrt[{4}]{x^{2}}})^{2}=({\sqrt[{6}]{x^{3}}})^{2}=\cdots

が成立しており、特に

x^{1/2}:={\sqrt {x}}

と定めることは（有理数として 1/2 = 2/4 = 3/6 = … のように同じものに無数の表示があるということと矛盾しないという意味で）well-defined で、（指数法則の成立などのいくつかの性質に関して）整合的である。

平方根函数

入力 x に対してその非負の平方根 √x を返す函数 f(x) = √x を非負実数全体の集合 R⁺ ∪ {0} 上で定義されていると考えた正の平方根函数

{\sqrt {}}\colon \mathbb {R} ^{+}\cup \{0\}\ni x\ {\xrightarrow {\text{1-1,onto}}}\ {\sqrt {x}}\in \mathbb {R} ^{+}\cup \{0\}

は（函数として well-defined で）、それ自身への全単射になる。正の平方根函数のグラフと負の平方根函数

{-{\sqrt {}}}\colon \mathbb {R} ^{+}\cup \{0\}\ni x\ {\xrightarrow {\text{1-1,onto}}}\ {-{\sqrt {x}}}\in \mathbb {R} ^{-}\cup \{0\}

のグラフを合わせたものは、二次函数 y = x² のグラフと直線 y = x に関して対称であるような放物線を成す。

正の平方根函数 √ は連続かつ至る所微分可能で

{\frac {d{\sqrt {x}}}{dx}}={\frac {1}{2{\sqrt {x}}}}

を満たし、原始関数のひとつは

\int {\sqrt {x}}\,dx={\frac {2}{3}}{\sqrt {x}}^{3}

で与えられる。また、収束冪級数としての二項展開

{\sqrt {1+x}}=\sum _{n=0}^{\infty }{\binom {1/2}{n}}x^{n}=1+{\frac {x}{2}}-{\frac {x^{2}}{8}}+\cdots

が |x| < 1 なるとき成立する。

x > 0 に対して自然数 n に関して帰納的に

f_{n}(x)={\sqrt {x+{\sqrt {x+{\sqrt {x+{\sqrt {x+...}}}}}}}}

（x および根号の個数は n）と定めると、函数列 f_n は漸化式

f_{n+1}(x)^{2}=x+f_{n}(x)

に従い、f_n(x) > 0 が α(x) > 0 に収束するならば α(x)² - α(x) - x = 0 でなければならないから、

\lim _{n\to \infty }f_{n}(x)={\sqrt {x+{1 \over 4}}}+{1 \over 2}

が成り立つ。

負の数の平方根

a が負の数のときは厄介な問題が生じる。平方根は実数の中には存在せず、複素数まで数の範囲を拡げると、 a の平方根、すなわち a = b² を満たすような b はふたつ存在するが、このふたつのうちのいずれを √a と定めるべきであるかということには必然的な答えを見出すことはできない。どちらを選んだのかを論理的に区別することができないのである。

b² = −1 の二つある根のうちどちらでもよいからひとつの解を i （虚数単位と呼ばれる）で表し、負の数 a に対して

{\sqrt {a}}={\sqrt {|a|}}\,i

とする。

このように定義すれば、b² = a の根は ±√a と求めることができる（a = −1 のとき √−1 = i だからこう定めることに矛盾はない）。しかしながら、i は b² = −1 の根であればどちらでもよかったこと、どちらを選んでももう一方の根は −i であることを考えれば、負の数 a に対する √a という記号は単独で 方程式 b² = a の根のいずれか一方を一意的に指し示すものではなく 、 i のとり方に依存してようやく一つの数を指し示している、ということが理解されなければならない。

次の誤った「証明」は興味深いものである。

-1=i\cdot i={\sqrt {-1}}\cdot {\sqrt {-1}}={\sqrt {(-1)\cdot (-1)}}={\sqrt {1}}=1

この証明において成り立たないのは三番目の等号である。つまり、

{\sqrt {a}}{\sqrt {b}}={\sqrt {ab}}

は一般には（特に $a,b$ 両方が負の場合）成り立たないのである。

二次体

必ずしも正とは限らない有理数全体 Q で定義される函数

\mathbb {Q} \ni x\mapsto {\sqrt {x}}\in \mathbb {A}

を考えるならば、その値域は（複素数となるものも含めた）代数的数（の一部）からなる。有理数の平方根が再び有理数となるならば、その有理数は（有理数の範囲での）平方数であるという。有理数内で平方数とならない有理数 d に対して √d は二次の無理数であって、Q に √d を付け加えて得られる体は二次体と総称される。

複素数の平方根

a が複素数のとき、代数学の基本定理によれば b² = a を満たす複素数は a に対して高々ふたつ存在する。0 でない a の極形式が

a=re^{i\theta }\quad (r>0,\,-\pi <\theta \leq \pi )

であるとき、r は正の実数であるからその正の平方根 √r が唯一つ定まり、複素数の平方が偏角を2倍にすることから、

{\sqrt {a}}={\sqrt {r}}\,e^{i\theta /2}

によって定義される複素数 √a は a のみによって一意的に定まり、√a² = a を満たす。これを a の平方根の主値（しゅち、principal value）という。この主値によって定義される平方根函数

\mathbb {C} \ni z\mapsto {\sqrt {z}}\in \mathbb {C}

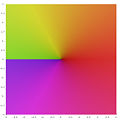
は、負の実軸上を除くガウス平面 C の全域で至る所正則である。しかし負の実軸上では連続でさえない。これを二枚のガウス平面を負の実軸で張り合わせた平方根函数のリーマン面上で考えるならば、至る所解析的である。

ガウス平面上の平方根函数を色で示したもの。原点の周りを偏角が正の方向にまわって、負の実軸を跨ぐときもう一枚のガウス平面へ跳ぶ（緑→緑）。
もう一枚のガウス平面上の平方根函数。こちらもやはり原点を正の方向にまわると、負の実軸を境に最初のガウス平面に帰る（紫→紫）。
原点付近での平方根函数のリーマン面（ガウス平面の張り合わせの様子）

なお、上記とはやや異なる観点から、 ${\sqrt {a+bi}}=c+di$ （ただし、a,b,c,dは実数とする。）とする式から、係数を比較して、複素数の平方根を求める手法に触れている文献がある。^[1]

脚注

^ ア・オ・ゲリファント、　ア・ゲ・クローシュ『方程式の解き方』東京図書株式会社、1995年、134頁

参考文献

一松信『√2の数学―無理数を見直す』海鳴社 ISBN 4875250568

外部リンク

数の泉（ ${\sqrt {2}}$ や ${\sqrt {3}}$ などを小数点以下100万桁まで掲載しているサイト）
資料庫（平方根）（ ${\sqrt {1}}$ から ${\sqrt {100}}$ までを小数点以下30桁まで掲載している）
Japanese soroban techniques - 加藤福太郎教授が考案した計算法（英語）

[1] ア・オ・ゲリファント、　ア・ゲ・クローシュ『方程式の解き方』東京図書株式会社、1995年、134頁

[1]

定義