固体核磁気共鳴

固体核磁気共鳴(こたいかくじききょうめい、固体NMR、英: Solid-state NMR, SSNMR)は、核磁気共鳴 (NMR) 分光法の一種。方向依存的な異方性相互作用の存在が特徴である。
概要[編集]
基本概念[編集]
スピンは磁場あるいは電場と相互作用する。空間的近接と2原子間の化学結合の両方あるいは一方は、核間の相互作用を生じさせる。一般的に、これらの相互作用は方向依存的である。全くあるいはほとんど流動性のない媒体(結晶、粉末、大きな膜ベジクル、分子集合体など)中では、異方性相互作用が核スピン系のふるまいについて実質的な影響を与える。対照的に、古典的な液体NMR実験では、ブラウン運動により異方性相互作用が平均化される。このような場合、これらの相互作用は、NMR実験のタイムスケールでは無視できる。
異方性核相互作用の例[編集]
固体NMRで一般的に見られる2つの方向依存性相互作用は、「化学シフト異方性」(chemical shift anisotropy; CSA) および核間「双極子カップリング」である。さらに多くのこのような相互作用が存在する。例えばNMRあるいは関連分野における異方性J結合、電子スピン共鳴 (ESR) におけるgテンソルなどである。数学的には、これらの相互作用は全て同じ形式で記述される。
実験的背景[編集]
異方性相互作用は、分子中の全ての部位の核スピンエネルギーレベルを修飾し、しばしばNMRスペクトルの線幅拡大の原因となる。しかしながら、異方性相互作用の存在を避けることができなかったり、あるいは異方性相互作用から興味のある分子における方向性情報といった構造パラメータを読み取れるため逆に望ましかったりと、様々な状況がある。
(広義の)固体における高分解能条件はマジック角回転 (magic angle spinning; MAS)、巨視的サンプル配向、これらの手法の組み合わせ、高粘度サンプル条件による流動性の向上、様々な高周波(ラジオ波、RF磁場)照射パターンを用いて確立することができる。後者はスピン空間において相互作用をデカップリングすることができるが、その他は実空間において相互作用の平均化を容易にする。加えて、巨視的不均一性からくる線幅拡大効果は適切なサンプル調製手法によって低減することができる。
デカップリング条件下では、例えば等方性化学シフトによって局所構造の等方性相互作用も観測される。加えて、デカップリングされた相互作用は選択的に再導入(リカップリング)することができ、例えば多くの構造パラメータを導きだすための位相の散逸の制御あるいは分極の伝達のために用いることができる、
固体NMRの線幅[編集]
回転速度5–15 kHzでのMAS条件下の13C核の残留線幅(半値全幅)は、通常0.5–2 ppmの程度であり、溶液NMR条件と同等である。しかしながら、20 kHzおよびそれ以上のMAS速度であっても、同種核双極子相互作用を経てリンクしているいくつかの核の非線形グループは部分的にしか抑制されないため、適切な溶液NMR条件をかなり越える0.5 ppmかそれ以上の線幅となってしまう。四極子相互作用といったその他の相互作用も相互作用の強さによって様々な度合いで線幅に影響を与える。一次の四極子広がりは十分速いMASによってかなり抑制されるが、二次の四極子広がりは異なる角度依存性を有しており一つの角度のみの回転では除去することができない。四重極核について等方性線幅を得る方法としては同時 (DOR) あるいは連続に2つの角度で回転させる方法や、MQMASあるいはSTMASといった二次元実験によって二次の四極子相互作用をリフォーカスする方法がある。
溶液NMRにおける異方性相互作用[編集]
溶液NMRの観点からは、配向媒体による双極子相互作用の運動平均化を低減することが望ましい。これらの残余双極子カップリング (residual dipolar coupling; RDC) の桁は通常、数rad/Hzのみであり、また高分解能条件を壊さない。これは様々な情報、特に互いの分子ドメインの配向に関するものを提供する。
双極子切り捨て[編集]
2つの核間の双極子カップリグは距離の三乗に反比例する。このため、双極子相互作用によって媒介される分極移動がこれらの核の一つが近接する3つ目の核(同様のもの全て、例えば13C)の存在によって切り捨てられる。この効果は一般的に双極子切り捨て (dipolar truncation) と呼ばれる。これは、生体分子の構造解析に必須である核間距離の効率的な抽出における主要な障害の一つとなっている。しかしながら、標識やパルスシークエンスを用いるなど数多くの方法によってこの問題を回避することが可能となってきている。
固体における核スピン相互作用[編集]
化学遮蔽[編集]
化学遮蔽はそれぞれの核の局所的な特性であり、外部磁場に依存する。
具体的には、外部磁場は分子軌道中の電子の電流を誘導する。これらの誘導電流は、しばしば分子構造全体に渡って影響を及ぼす局所磁場を作る。そのため違った分子環境にある核は大抵、この効果から独自の局所磁場を経験する。
十分に速いマジック角回転下あるいは溶液NMRでは、化学シフトの方向依存的特徴は除去され、等方性化学シフトが残る。
Jカップリング[編集]
Jカップリングあるいは間接的核スピン-スピン相互作用(Jは実際はテンソル量であるにもかかわらず「スカラー」カップリングとも呼ばれることがある)は、化学結合を通した核スピンの相互作用である。
双極子カップリング[編集]

核スピンは双極子モーメントを示し、他の核の双極子モーメントと相互作用する。相互作用の強度はスピン種や核間距離、外部磁場 B(図を参照)に対する2つの核スピンを繋ぐベクトルの配向に依存している。最大双極子カップリングは双極子カップリング定数 d によって与えられる。
rは核間距離、γ1およびγ2は核の磁気回転比である。強い磁場中では、双極子カップリングは外部磁場に対する核間ベクトルの配向に依存する。
その結果として、双極子カップリングベクトルが強い外部磁場に対する角度θm=54.7°(Dがゼロになる角度)にある2つの核は、双極子カップリングがゼロになる。θmはマジック角と呼ばれる。少くともある程度双極子カップリングを除去する一つの手法がマジック角回転である。
四極子相互作用[編集]
1/2より大きいスピンを持つ核は非球状の電荷分布を持つ。これは四極子核として知られている。非球状電荷分布は、ある種の非対称性(例えば三角形結合原子では平面中の原子周囲には電子が存在するが、上下には存在しない)電場勾配と相互作用でき、ゼーマン効果に加えてエネルギーレベルの変化を生み出す。四極子相互作用は、ジーマン相互作用は別にするとNMRにおける最大の相互作用であり、その大きさは同程度になることさえある。
この相互作用がとても大きいため、その他のほとんどの相互作用のように一次のみで扱うことができない。これは、それぞれ別に扱うことができる一次と二次の相互作用があることを意味している。一次相互作用は磁場に対して角度依存的であり(、P2ルジャンドル多項式)、これはサンプルを (~54.74°) で回転させることで一次相互作用を平均化できることを意味している(ゼーマン、化学シフト、常磁性、J結合相互作用以外のその他全ての相互作用もまた角度依存的である)。しかしながら、二次相互作用はP4ルジャンドル多項式に依存し、そのゼロ点は30.6°および70.1°である。これらは同時に2つの角度で回転させるDOR (DOuble angle Rotation) あるいは2つの角度を素早く入れ換えるDAS (Double Angle Spinning)[2] を使用することによってうまく出し抜くことができる。このような実験のために特殊化された機器(プローブ)が開発されている。革命的な進歩はLucio Frydmanが1995年に発表したの多量子マジック角回転 (multiple quantum magic angle spinning; MQMAS) NMRであり、これによって四極子角の高分解能固体NMRスペクトルを常法によって得ることが可能になった[3][4]。MQMASと類似した手法として、2000年にZhehong Ganによって提唱されたサテライト遷移マジック角回転 (satellite transition magic angle spinning; STMAS) NMRがある[5]。
その他の相互作用[編集]
常磁性物質はナイトシフトの影響下にある。
歴史[編集]
パーセル、Torrey、Pound: 1945年パラフィン中の1Hにおける「核誘導」の発見、ほぼ同時にBlochらによって水中の1Hでも観測された。
最新の固体NMR分光法[編集]
基本例[編集]
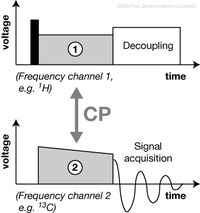
ほとんどの固体NMR実験における基本RFパルスシークエンスおよびビルディングブロックは交差分極 (cross-polarization; CP) によって始まる[6]。交差分極は低磁気回転比を持つ核(例えば13Cや15N)の信号を増強するためや、スペクトル編集手法(例えばタンパク質分光法における15N→13C向きの交差分極)として使用できる。磁化移動を起こすには、2つの周波数チャネルで印加されたRFパルスはハートマン–ハーン条件を満たさなければならない[7]。MAS下では、この条件はRFコイルの電圧とサンプル回転の速度の相関を定義する。こういった条件の実験最適化は(固体)NMR実験を行う上での日常的な仕事の一つである。
CP-MASは固体NMR分光法におけるほとんどのパルスシークエンスの基本ビルディングブロックである。その重要性から、1Hスピン分極の直接励起に続く13C、15Nあるいは同様の核へのCP移動ならびにこれら核のシグナル検出に用いられるパルスシークエンスは、「CP実験」あるいはMASと繋げて「CP-MAS」としばしば呼ばれる[8]。これが固体NMR分光法を用いた解析の典型的な出発点である。
デカップリング[編集]
核スピン相互作用は、NMRスペクトルの分解能を向上しスピン系を単離するために除去(デカップリング)しなければならない。
化学シフト異方性および双極子カップリングを実質的に低減あるいは除去することができる手法は「サンプル回転」(最も一般的なマジック角回転、あるいはオフ-マジック角回転[2])である。
「同種核RFデカップリング」は検出するものと同じ核のスピン相互作用をデカップリングする。「異種核RFデカップリング」は他の核とのスピン相互作用をデカップリングする。
リカップリング[編集]
線幅の拡がりは多くの場合望ましくないが、結晶格子中の原子間の双極子相互作用は非常に有用な情報を与える。双極子カップリングは距離依存的であるため、同位体標識した分子中の原子間距離を算出するために使用できる。
ほとんどの双極子相互作用はサンプル回転によって除去されるため、望む双極子相互作用を観測できるように再導入するためにはリカップリング実験が必要である。
リカップリング実験の一例は、回転エコー二重共鳴 (Rotational Echo DOuble Resonance; REDOR) 実験である[9]。これは、アモルファス固体などのNMR結晶研究の基礎ともなる。
応用[編集]
生物学[編集]
膜タンパク質およびアルツハイマー病やパーキンソン病と関連しているアミロイド繊維(フィブリル)は、固体NMR分光法が溶液NMR分光法およびビーム回折法(例えばX線結晶構造解析や電子顕微鏡法)を補完する2つの応用例である。
化学[編集]
固体NMR分光法は有機化学および無機化学において解析ツールとして役立っている。SSNMRはまた様々な系の局所的な動力学、反応速度、熱力学を研究するための有益なツールである。
脚注[編集]
- ^ National Ultrahigh-field NMR Facility for Solids. “900 MHz Bruker Avance II NMR spectrometer”. 2011年11月11日閲覧。
- ^ a b Qian C, Pines A, Martin RW (2007). “Design and construction of a contactless mobile RF coil for double resonance variable angle spinning NMR”. J. Magn. Reson. 188 (1): 183-189. doi:10.1016/j.jmr.2007.06.006. PMID 17638585.
- ^ Lucio Frydman and John S. Hardwood (1995). “Isotropic Spectra of Half-Integer Quadrupolar Spins from Bidimensional Magic-Angle Spinning NMR”. J. Am. Chem. Soc. 117: 5367—5368. doi:10.1021/ja00124a023.
- ^ D. Massiot, B. Touzo, D. Trumeau, J. P. Coutures, J. Virlet, P. Florian and P. J. Grandinetti (1996). “Two-dimensional Magic-Angle Spinning Isotropic Reconstruction Sequences for Quadrupolar Nuclei”. Solid-State NMR 6: 73-83. doi:10.1016/0926-2040(95)01210-9. PMID 8925268.
- ^ Zhehong Gan (2000). “Isotropic NMR Spectra of Half-Integer Quadrupolar Nuclei Using Satellite Transitions and Magic-Angle Spinning”. J. Am. Chem. Soc. 122 (13): 3242–3243. doi:10.1021/ja9939791.
- ^ Pines A., Gibby M. G., Waugh J. S. (1973). “Proton-enhanced NMR of dilute spins in solids”. J. Chem. Phys. 59: 569-590. doi:10.1063/1.1680061.
- ^ Hartmann S. R., Hahn E. L. (1962). “Nuclear Double Resonance in the Rotating Frame”. Phys. Rev. 128: 2042-2053. doi:10.1103/PhysRev.128.2042.
- ^ Schaefer, J. and Stejskal, E. O. (1976). “Carbon-13 Nuclear Magnetic Resonance of Polymers Spinning at the Magic Angle”. J. Am. Chem. Soc. 98: 1031-1032. doi:10.1021/ja00420a036.
- ^ Gullion, T. and Schaefer, J. (1969). “Rotational-Echo, Double-Resonance NMR”. J. Magn. Reson. 81: 196-200. doi:10.1016/0022-2364(89)90280-1.
初心者向け推薦文献[編集]
- “High Resolution Solid-State NMR of Quadrupolar Nuclei” (PDF). Grandinetti ENC Tutorial. 2011年11月11日閲覧。
- David D. Laws, Hans-Marcus L. Bitter, and Alexej Jerschow (2002). “Solid-State NMR Spectroscopic Methods in Chemistry”. Angew. Chem. Int. Ed. 41: 3096. doi:10.1002/1521-3773(20020902)41:17<3096::AID-ANIE3096>3.0.CO;2-X.
- Levitt, Malcolm H. (2001). Spin Dynamics: Basics of Nuclear Magnetic Resonance. Chichester, United Kingdom: Wiley(固体NMRを含むNMRの基礎)
- Duer, Melinda J. (2004). Introduction to Solid-State NMR Spectroscopy. Oxford: Blackwell (固体NMR分光法の詳細な例)
上級者向け文献[編集]
専門書および総説
- McDermott, A. (2009). “Structure and Dynamics of Membrane Proteins by Magic Angle Spinning Solid-State NMR”. Annu. Rev. Biophys. 38: 385-403. doi:10.1146/annurev.biophys.050708.133719. PMID 19245337.
- Mehring, M. (1983). Principles of High Resolution NMR in Solids (2nd ed. ed.). Heidelberg: Springer
- Slichter, C. P. (1990). Principles of Magnetic Resonance (3rd ed. ed.). Heidelberg: Springer
- Gerstein, B. C. and Dybowski, C. (1985). Transient Techniques in NMR of Solids. San Diego: Academic Press
- Schmidt-Rohr, K. and Spiess, H.-W. (1994). Multidimensional Solid-State NMR and Polymers. San Diego: Academic Press
- Dybowski, C. and Lichter, R. L. (1987). NMR Spectroscopy Techniques. New York: Marcel Dekker
- Ramamoorthy, A. (2006). NMR Spectroscopy of Biological Solids. New York: Taylor & Francis
一般[編集]
参考書および論文
- Andrew, E. R., Bradbury, A. and Eades, R. G. (1959). “Removal of Dipolar Broadening of Nuclear Magnetic Resonance Spectra of Solids by Specimen Rotation”. Nature 183: 1802-1803. doi:10.1038/1831802a0.
- Richard R. Ernst, Geoffrey Bodenhausen, Alexander Wokaun (1990). Principles of Nuclear Magnetic Resonance in One and Two Dimensions. International series of monographs on chemistry 14 (2nd ed.). Clarendon Press. ISBN 9780198556473
- Hartmann S. R., Hahn E. L. (1962). “Nuclear Double Resonance in the Rotating Frame”. Phys. Rev. 128: 2042-2053. doi:10.1103/PhysRev.128.2042.
- Pines A., Gibby M. G., Waugh J. S. (1973). “Proton-enhanced NMR of dilute spins in solids”. J. Chem. Phys. 59: 569-590. doi:10.1063/1.1680061.
- Purcell, E. M.; Torrey, H. C.; Pound, R. V. (1946). “Resonance Absorption by Nuclear Magnetic Moments in a Solid”. Phys. Rev. 69 (1-2): 37–38. doi:10.1103/PhysRev.69.37.
- Schaefer, J. and Stejskal, E. O. (1976). “Carbon-13 Nuclear Magnetic Resonance of Polymers Spinning at the Magic Angle”. J. Am. Chem. Soc. 98: 1031-1032. doi:10.1021/ja00420a036.
- Gullion, T. and Schaefer, J. (1969). “Rotational-Echo, Double-Resonance NMR”. J. Magn. Reson. 81: 196-200. doi:10.1016/0022-2364(89)90280-1.
- MacKenzie, K. J. D and Smith, M. E. (2002). Multinuclear Solid-State NMR of Inorganic Materials. Pergamon Materials Series Volume 6. Oxford: Elsevier.
外部リンク[編集]
- SSNMRBLOG Solid-State NMR Literature Blog by Prof. Rob Schurko's Solid-State NMR group at the University of Windsor
- www.ssnmr.org Rocky Mountain Conference on Solid-State NMR




