一筆書き

一筆書き(ひとふでがき)とは、広い意味では「筆記具を平面から一度も離さず線図形を描く」ことである。狭い意味では、これに加えて「同じ線を二度なぞらない(点で交差するのはかまわない)」という条件が加わる。
以下は後者の狭い意味での一筆書きについて記す。
三角形「△」や四角形「□」は一筆書き可能だが、十字「+」は一筆書きできない。また、五芒星や白星「☆」、六芒星「✡」は一筆書き可能だが、アスタリスク「*」は一筆書きができない。このように、一筆書きできる図形とできない図形がある。
「与えられた図形が一筆書き可能かどうか」という問題の例として、「ケーニヒスベルクの橋の問題」(独: Königsberger Brückenproblem)が知られている。なお、ケーニヒスベルクとは実際にあった場所の名前である。
ケーニヒスベルクの七つの橋問題[編集]
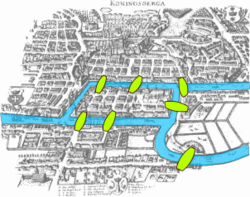
現在のケーニヒスベルクの橋のLink(現在は、橋の本数が過去とは異なる)
問題[編集]
18世紀の初め頃にプロイセン王国の東部、東プロイセンの首都であるケーニヒスベルク(現・ロシア連邦カリーニングラード)という大きな町があった。この町の中央には、プレーゲル川という大きな川が流れており、七つの橋が架けられていた。あるとき町の人が、次のように言った。
「このプレーゲル川に架かっている7つの橋を2度通らずに、全て渡って、元の所に帰ってくることができるか。ただし、どこから出発してもよい」
町の人が言ったことはできるだろうか。
グラフ理論との関連[編集]
1736年、レオンハルト・オイラーは、この問題を以下のグラフに置き換えて考えた。
このグラフが一筆書き可能であれば、ケーニヒスベルクの橋を全て1度ずつ通って戻ってくるルートが存在することになる。
そして、オイラーは、このグラフが一筆書きできないことを証明し、ケーニヒスベルクの問題を否定的に解決したのである。
他の解法[編集]
問題として示されている範囲の枠外にいったん出ると、その枠外で任意の経路をとることができるため、「指定された橋を全て1度ずつ通って戻ってくるルート」をとることも可能となる。ただし、いわゆる「題意」からは外れる。
一筆書き可能かどうかの判定法[編集]
ある連結グラフが一筆書き可能な場合の必要十分条件は、以下の条件のいずれか一方が成り立つことである(オイラー路参照)。
一筆書きの解法[編集]
- すべての頂点の次数が偶数 →ある頂点から出発し、元の頂点に戻り、さらにその頂点から出発し、元の頂点に戻る順路を考える。もし、まだ通っていない経路があれば、先ほどの順路からある頂点を選び、そこから寄り道をしてその頂点に戻ってくる順路を付け足したものに修正する。その修正を繰り返せばよい。
- 次数が奇数の頂点の数が2で、残りの頂点の次数は全て偶数 →ある奇点から出発し、もう一方の奇点へ抜ける順路を考える。もし、まだ通っていない経路があれば、先ほどの順路からある頂点を選び、そこから寄り道をしてその頂点に戻ってくる順路を付け足したものに修正する。その修正を繰り返せばよい。
鉄道における「一筆書き」[編集]

日本の鉄道旅行(主にJRグループの路線)において、目的地まで最短経路で移動・往復するのでなく、出発地やその近くまでの大回りきっぷを購入することを比喩的に「一筆書き」と呼ぶことがある[1]。
ただし実際には、きっぷの規則は「同じ駅を2度通過してはいけない」という原則によっており、この記事で説明しているオイラー路である「一筆書き」ではなく、グラフ理論ではハミルトン路と呼ばれているものの規則に近い。
最長片道切符などの途中下車扱いで主な目的地に立ち寄ったり(運賃の遠距離逓減制で割安になることが多い)、娯楽として大都市近郊区間の大回り乗車を楽しんだりする。
脚注・出典[編集]
- ^ 【知っとくトク】鉄道でぐるり一筆書き 長距離は運賃安く 途中下車も可能『日本経済新聞』夕刊2018年4月23日(くらしナビ面)
関連項目[編集]
- グラフ理論
- 橋づくし
- 大都市近郊区間 (JR) - 同じ駅・区間を二度通らずに長い経路をとって隣の駅まで乗車する「大回り乗車」ができる。
- 最長片道切符 - 同じ駅・区間を二度通らずにとることのできる最も長い経路(主にJRグループ)。


