モアレ
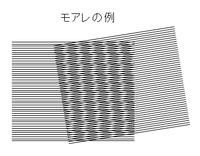  |
モアレまたはモワレ(仏: moiré)は、干渉縞ともいい、規則正しい繰り返し模様を複数重ね合わせた時に、それらの周期のずれにより視覚的に発生する縞模様のことである。
また、規則正しい模様を、デジタル写真などのビットマップ画像にした場合も、画像の画素解像度と模様の周波数のずれが原因で同様の縞模様が発生するがこれもモアレと呼ぶ。また印刷でも網点という点の集まりに画像を変換するので同様の現象が発生する。(これらの詳細は下記参照)
モアレそのものも周期を持ち、この周期は元になる模様の周期の組み合わせで決まる。物理学的にいうと、モアレとは二つの空間周波数のうなり現象といえる。様々な形態で発生するため、モアレにもいろいろなものがある。モアレを望ましからぬものとして取り除く対象にする場合もあり、逆に発生したモアレを有用なものとして利用する分野もある。
概要[編集]
図1のように2組の平行模様を斜めに重ねると交差部分が平行線の周期とは異なる縞模様になる。これがモアレの代表的な例である。 モアレは平行線でなく、碁盤の目のような平面パターンでも発生する。たとえば、升目のピッチが異なる二つの市松模様を重ねると発生する。図2に縦横に並んだ模様(金属板に開いた丸穴)の重なりによるモアレの例を示す。これは二次元空間周波数のうなりである。この効果は印刷分野や画像処理分野では特に注意を要するものである。
モアレの実例[編集]
モアレを利用した測定[編集]
モアレは迷惑な現象だけではなく、これを積極的に利用することもある。高精度の位置決め用の位置センサの一種モアレスケールでは、わずかにピッチを変えた平行縞を重ねたときに発生するモアレが、二つの平行縞の相対変位よりも大きく移動することを利用し、変位を拡大して測定するものである。また、立体の表面に二つの格子縞を投影したときに発生する干渉縞の形状(等高線)から物体の立体形状を得る方法を、モアレトポグラフィという。脊柱検査の一環でモアレ撮影(検査)にモアレ写真法が使われる。
印刷[編集]

印刷では、写真のような階調を表現するために、網点を用いる。すなわち色の濃さを規則正しく配置された点それぞれの大きさで表現する。このため、印刷された写真をもとに原版を作成して再び印刷すると、網点のピッチの違いや、ピッチが同じでもわずかな傾きによってモアレが発生することがある。またカラー印刷では、複数の色版の網点を重ねて印刷するため、周期的な色模様がみえる場合がある。このため、各版はモアレが最も目立たないとされる角度に網点を傾けて印刷している。 単色では45度、CMYKでは、モアレが目立つCMKの3色のうち1色を45度に置き、これに対して他の版をそれぞれ30度ずつ離しておくのが伝統的な角度である。そしていずれか2色の中間にモアレがめだちにくいY版を置くようにする。(例としてM版を15度、K版を45度、C版を75度、Y版を30度)。モアレの出た写真は極めて見栄えが悪いため印刷においては注意して避けるべき点の一つである[1]。
画像処理[編集]


コンピュータによる画像処理においても、画像は画素とよばれる縦横に周期的に配置した点に分解して表現することから、印刷と同様なモアレが発生する可能性がある。
画像処理の過程では、縦横画素数を整数分の1以外の大きさに縮小・変形した場合に発生しやすい。グラフィックソフトウェアにおいて縮小が単なる間引き処理であると、ありもしない模様が発生 (偽解像) する。これは折り返し雑音の一種である。これを防ぐためには、縮小後の画素位置周辺の縮小前の複数画素からの距離と強度で重み付けするリサンプリング処理などが有効である。
デジタルカメラでは、画素が縦横に規則的に配列されているため、画素ピッチの1/2を超えるピッチの明暗模様を撮影すると偽解像する。レンズの解像度がこれより低い場合や光路で干渉によるボケ (小絞りボケなど) が生じる場合は問題にならないが、一般的にこれを解決するアプローチとして、撮像素子の手前にローパスフィルタ (画素ピッチ程度にぼかすフィルタ) を入れるのが普通である。なおフィルムカメラでは、画素にあたる感光粒子が不規則に配列しているため、この問題は生じない。
網点印刷された写真などをスキャナで入力する場合にも、写真とスキャナの分解能の差次第でモアレが発生する。スキャナの光学的な分解能が高い場合には、網点のピッチ以上の解像度でスキャンした後、グラフィックソフトウェアにおいて必要とする分解能まで落とす (間引きではなく補間する) アプローチが有効である。例えば縦3000pxでスキャンした画像を、縦1600pxの解像度のモニターで見るとモアレが発生するため、画像の解像度を縦1500~1600px程度まで落とすことでモアレを回避できる。
表示においては、処理する解像度と表示する解像度が異なる場合にも発生することがある。グラフィックソフトウェアなどで縮小表示するときに、やはり表示分解能で補間するフィルタ処理が必要であるが、高速表示のためにこれを省いているグラフィックソフトウェアも多い。
テレビ[編集]
テレビでも走査線が上下方向に周期的にならぶため画像処理と同様な問題がある。
さらにアナログテレビ、特にNTSCカラー方式においては、輝度信号において細かな模様を伝送する高周波領域と、色差信号とが、クシ状に交互に重畳されているため、信号の干渉により色付きのモアレ状の画質劣化が発生する。これはモアレ現象というよりカラー方式の信号処理の限界から来る現象で、クロスカラー妨害と呼ばれる。
アナログ方式のVTRでは、記録時の時間軸のわずかな揺れ(ジッタ)によって色がわずかに変動し、これがモアレ状の画質劣化として感知されることがある。
繊維・衣服[編集]
繊維分野で、布・織物を構成する繊維の不規則性から波型模様が生ずることがあるが、これが「起源」の項でしめすモアレの語源である。織機の動作不良や保存方法の問題などによって起こり、布製品の均一性を損なうため望ましくないものである。しかし絹織物などで意図的に美しい模様を発生させて用いる例もある。
漫画[編集]
漫画制作においては、異なる複数の規則的な模様のスクリーントーンを重ねた際にモアレが生じる。乱れとして避けられることが多いが、一方で演出として意図的に用いる制作者もいる。
医学[編集]
1980年から脊柱検査の一環でモアレ撮影(検査)が行われている。
起源[編集]

モアレの元来の意味は織物(古くは絹織物であるが、毛織物や合成繊維にも用いられる)にあらわれた波型の模様で、杢目模様(もくめ~)あるいは水模様という。このパターンはふたつ、あるいはそれ以上の平行な繊維を重ねることにより発生するものである。
モアレという語はもともとアラビア語/ペルシア語でアンゴラ羊の毛織物製の衣料を意味する。英語に取り入れられた後、フランス語にも mouaire として登場する。1660年には英語に再輸入されて moire あるいは moyre となった。一方フランス語では mouaire が動詞 moirer(巻きずれや圧力で水模様を発生させる)に変化し、1823年には形容詞 moire を派生させた。英語では moire と moiré とは同義語として扱われている。
計算[編集]
平行パターン[編集]
幾何学的方法[編集]

ふたつの、平行かつ等間隔なパターンを考える。第一パターンの間隔をp、第二パターンの間隔をp+δpとする。ただし、0<δp<pである。
図の左端でふたつのパターンの線が重ね合わせられたとしたら、右にいくほどずれは増加していく。ある数だけ右にいくと、パターンは「向かい合う」。つまり、第二パターンの線は第一パターンの線の間に位置する。これを遠くから眺めたとすると、線が重なり合っている部分は空白が広く見えるため淡く見え、線が向かい合っている部分は暗く見える。
ひとつめの暗部の中間点は、ずれがp/2に等しくなった点である。第二パターンのn番目の線は、第一パターンの線からn・δpだけずれているので、ひとつめの暗部の中間点は、
- n・δp = p/2
に相当する。すなわち、
である。淡部と暗部の中間点の距離dは、
であり、ふたつの暗部の中間点の距離(もしくは淡部の中間点の距離)は、
である。この式から、次のことがわかる。
- 線間隔が大きいほど、淡部と暗部の距離は大きくなる。
- ずれδpが大きいほど、淡部と暗部の距離は小さくなる。つまり、淡部と暗部が大きく離れているということは、ふたつのパターンの間隔が近いということになる。
もちろん、δp = p/2のときは、コントラストのない一様に灰色な図が得られる。
モアレの原理はノギスに類似している。
干渉による方法[編集]
コントラストIが正弦関数で変化するような、透明なパターンをふたつ考える。
間隔はそれぞれp1 = 1/k1およびp2 = 1/k2である。これらが重ね合わせられたとき、結果として得られる明度(干渉)は
が得られる。これより、明度はふたつの三角関数の合成であることがわかる。正弦関数に係る部分は高周波成分であり、ふたつのパターンの空間的振動数の平均となっている。余弦関数に係る部分は低周波成分で、ふたつのパターンの空間的振動数の差の半分となっている。低周波成分は高周波成分の「包絡線」となっている。この成分の波長λは空間的振動数の逆数であり、
p1 = p、p2 = p+δpとおくと、
が得られる。 この包絡線のゼロ点間の距離はλ/2であり、最大点間の距離もまたλ/2である。ここで前述した幾何学的方法と同じ結果が得られたが、p/2だけずれている。このずれはどちらのパターンを基準とするかに結びついている不確定性で、δp << pのとき無視できる。
この現象はストロボスコープに類似している。








