接触 (数学)

数学において二つの函数が点 P において k-次の（あるいは k-位の）接触（せっしょく、英: contact）をなすとは、P においてそれらの値および k-階までの導函数の値が一致するときに言う。これは同値関係をなし、その同値類は一般にジェットと呼ばれる。

点における高次の接触は、曲線などの幾何学的対象についても定義される（ここに、微分は弧長変数に関するものを考える）。この場合には、接触は接吻 (osculation, kissing) とも呼ばれ、接する (tangent) という性質を一般化するものである。

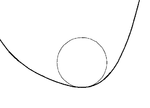
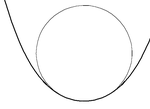
曲線とその上の点が与えられたとき、ある固定した曲線族に属する接触曲線とは、その曲線上の点において曲線族の中で可能な最も高次の接触を持つ曲線を言う。例えば接線は、直線族に属する接触曲線として、与えられた曲線と一次の接触を持つものである。また例えば曲線の接触円は、円族の中で、与えられた曲線と二次の接触をなす（接触角が一致し曲率も等しい）ものを言う。他も同様。

接触形式は、奇数次元多様体上で定義される特定の一次微分形式を言う（接触幾何学を参照）。接触変換は座標変換と関係し、古典力学において重要である（ルジャンドル変換の項を参照せよ）。

多様体同士の接触はしばしば特異点論において研究され、そこでの接触の分類として A-系列（A₀: 交点, A₁: 接点, A₂: 接吻点, …）に加えて、球面と高次の接触を持つことによって定義される臍点を含む D-系列がある。

曲線と円との一次の接触 (tangent)

曲線と円との二次の接触 (osculating)

曲線と円との、曲線の頂点における、三次の接触

曲線同士の接触

二つの平面曲線が点 p において交わるとき、

• 零次の接触をなすとは、それら曲線が p において単に交わることをいう（接線が存在する必要はない）
• 一次の接触をなすとは、それら曲線が p において接する (tangent) ときに言う。
• 二次の接触をなすとは、それら曲線の p における曲率が等しいときに言う。またそのような曲線たちは p において接吻する (osculate) と言う。
• 三次の接触をなすのは曲率の微分が等しいときである。
• 四次の接触をなすのは曲率の二階微分が等しい時である。

曲線と円との接触

滑らかな平面曲線 S 上の各点 S(t) に対して、ちょうど一つの接触円（その半径は S の t における曲率 κ(t) の逆数）が存在する。曲率が零の点（つまり曲線の変曲点）では接触円は直線となる。各点における接触円の中心（曲率中心）の軌跡は、その曲線の縮閉線である。

曲率の微分 κ′(t) が零ならば、接触円は三次の接触をなし、曲線はその点において頂点を持つという。このとき、縮閉線は接触円の中心において尖点を持つ。またこの時の曲率の二階微分の符号が、その曲線の曲率が極小となるか極大となるかを決定する。任意の閉曲線が、少なくとも四つの頂点を持ち、そのうち二つは最大点、二つは最小点である（四頂点定理）。

一般に、一つの曲線が任意の円と四次の接触を持つことはない。しかし曲線の一径数族との四次の接触が生成的に生じ、それは二つの頂点（極大点と極小点）を零化する。そのような点において曲率の二階微分は零である。

参考文献

• 矢野健太郎『微分積分学』裳華房、1956年。 
• Bruce, J. W.; P.J. Giblin (1992). Curves and Singularities. Cambridge. ISBN 0-521-42999-4 
• Ian R. Porteous (2001) Geometric Differentiation, pp 152–7, Cambridge University Press ISBN 0-521-00264-8 .