シュタイナーの円鎖

幾何学において、シュタイナーの円鎖（しゅたいなーのえんさ^[1]、英語: Steiner chain）または シュタイナー環^[2]、シュタイナーの円環^[3]、シュタイナー円鎖^[4]^[5]^[6]は、 $n$ 個の円が2つの交わらない円と円鎖の前と次の円に接しているとき、その $n$ 個の円を指す用語である^[7]。ただし $n$ は有限の整数であるとする。特に円鎖が閉じる（closed chains）とは最初の円と最後（ $n$ 個目の円）が接する状態にある、ということである。逆にopen chains とは、そうでない場合を表す。シュタイナーの円鎖の2つの円（図1の赤と青の円）の条件は円 $α,β$ が交わっていないことだけである。つまり、一方の円がもう一方の円の内部になければならないということはない。シュタイナーの円鎖の円の中心の軌跡は、一方の円がもう一方の円の内部にあるならば楕円を、そうでないならば双曲線を成す。

シュタイナーの円鎖はヤコブ・シュタイナーに因み名づけられた。彼の功績の一つにSteiner's porismと呼ばれる以下の様に定義される図形がある。

2つの円

α,β

に対して、

n

個の円の閉じているシュタイナーの円鎖が一つでもあれば、

n

個の円の閉じているシュタイナーの円鎖は無数に見つけることができる。そして

α,β

に接する円はすべて、そのようなシュタイナーの円鎖の一つになり得る^{[注釈 1]}。

反転幾何学はシュタイナーの円鎖をうまく扱うのに有用である。反転は交点、角、円を一対一対応させるため、 $n$ 個のシュタイナーの円鎖を反転させると、シュタイナーの円鎖は別の $n$ 個の円に移る。ある円における反転は円 $α,β$ を同心円に変換し、その変換によってとシュタイナーの円鎖のすべての円は同じ大きさになり、玉軸受のようにアニュラス上を"転がる"ことができる。この構成がシュタイナーの円鎖の様々な性質をもたらしている。たとえば、シュタイナーの円鎖の円同士の接点は常に共円である。シュタイナーの円鎖の一般化には例えばソディの六球連鎖やパップス円鎖がある。

定義と接し方の種類[編集]

シュタイナーの円鎖の接し方の違い
7円のシュタイナーの円鎖 (黒)。赤い内部の円に外接し青い外部の円に内接している。
7円のシュタイナーの円鎖 (黒)。青と赤どちらの円にも外接している。
8円のシュタイナーの円鎖 (黒)。青と赤どちらの円にも内接している。

2円 $α,β$ が交わっていなければ円の配置は、小さい方の円は、大きい方の円の内部にあるか、外部のあるかのみである。この2円は基本アニュラスのように小さい円が大きい円の内部にある場合で示される。この構成ではシュタイナーの円鎖は内側の円に外接し、外側の円に内接している。しかし、小さい方の円が大きい円の外部にある場合も存在する。この場合も、シュタイナーの円鎖の条件を満たし、元の2円に外接のみ、または内接のみするようになる。元の2円が接している場合は円鎖は無限となりアルベロスとともに議論されることが多い（パップス円鎖）。

閉じている、開いている円鎖[編集]

9つの円の円鎖が閉じている。
9つの円の円鎖が開いていて、一部が重なっている。
17つの円が二周することで多環を成している。

2つの円 $α,β$ は $n$ 個のシュタイナーの円鎖の円と接しているが、 $n$ 個の各円 $C k$ は $α,β$ と両隣の円の4つとしか接していない。普通はシュタイナーの円鎖が閉じている場合を議論するがそうでない場合、つまり $C 1, C n$ が接さない場合、 $C 1, C n$ は3円とだけ接することとなる。多環のシュタイナーの円鎖ではその円鎖が閉じる前にさらに何周かすることとなる。

シュタイナーの円鎖は双角錐におけるcircle packing theorem（英語版）の系である。

アニュラスと条件[編集]

アニュラスにおけるシュタイナーの円鎖
n = 3
n = 6
n = 9
n = 12
n = 20

シュタイナーの円鎖のもっとも簡単な場合は、2つの円 $α,β$ が同心円であるときである。 $α,β$ の中心を $O$ とする。 $n$ 個のシュタイナーの円鎖について、2円 $α,β$ の大きい方の半径を $R$ 、小さい方の半径を $r$ 、隣り合うシュタイナーの円鎖の円の中心を $O i, O i +1$ として対称性より、 $∠ O i OO i +1 =2 θ =360°/ n$ である。また隣り合うシュタイナーの円鎖の円は接するのでその円の中心の距離は円の半径 $ρ$ の2倍に等しい。図のように $∠ O i OO i +1 =2 θ$ の角の二等分線は2つの直角三角形をつくるので $θ =180°/ n$ として、その正弦を求めることができる。

\sin \theta ={\frac {\rho }{r+\rho }}

よって $ρ$ について整理して以下の式を得る。

\rho ={\frac {r\sin \theta }{1-\sin \theta }}

シュタイナーの円鎖とそれぞれ $α,β$ の接点と、 $α,β$ の中心は明らかに共線であるからR = r + 2ρが従う。

この等式は、シュタイナーの円鎖ができる条件を与える。 $n$ 個のシュタイナーの円鎖ができる条件は、2円の半径 $R,r$ が以下の式を満たすことである。

{\frac {R}{r}}=1+{\frac {2\sin \theta }{1-\sin \theta }}={\frac {1+\sin \theta }{1-\sin \theta }}=\left[\sec \theta +\tan \theta \right]^{2}

下記の様に、半径の比は2円の反転距離（英語版）によって、任意の円に拡張することができる。

\delta =\ln {\frac {R}{r}}

同心円上の2円についての解法を使って、一般の位置にある2円に対する $n$ 個のシュタイナーの円鎖ができる条件は以下の様にまとめられる。

\delta =2\ln \left(\sec \theta +\tan \theta \right).

$n$ 個のシュタイナーの円鎖が多環であるときは、アニュラスを $m$ 周するとして隣り合うシュタイナーの円鎖の円の中心の成す中心角が以下を満たせばよい。

\theta ={\frac {m}{n}}180^{\circ }

別の言い方をすれば、シュタイナーの円鎖のできる条件は不変であるということである。

反転下での性質[編集]

シュタイナーの円鎖の反転したものの性質
2円（桃と水）は元の円の両方に内接する。それらの円の中心は円の交点の成す中心角が $2 θ$ ならば、 $α,β$ の中心と共線である。
反転した図では、広義の円は広義の円へと移り、交点や角度を保つ。茶色の円は $α,β$ と直交している。
2つのシュタイナーの円鎖の隣り合う円の接点を通る円は最初の二2円に直交する。
2つのシュタイナーの円鎖と与円の接点を通る円は元の2円に直交する。

円による反転はシュタイナーの円鎖を、同数の円を持つ他の図形に変換する。

円鎖の反転で、隣り合う円が接するという事実は変わらない。また、与円が同心円になるよう反転したとき、シュタイナーの円鎖の隣り合う円の接点は与円を反転したものの中間上にある。したがってシュタイナーの円鎖で、隣り合う円との接点は同一円周上にある。この方法はパップス円鎖にも適応できる。

反転された円鎖では、 $α,β$ の中心 $O$ からシュタイナー円鎖の円への接線は等角度で離れている。これは元の円鎖において反転の中心を通るシュタイナー円鎖の円の接線の成す角が常に等しいことを示している。

円鎖の反転で、元の円とシュタイナーの円鎖を成す円の接点と、その反対側の接点を結ぶ $n$ 本の直線はすべて一点 $O$ で交わる。同様に接点における接線も $O$ で交わる。反転の中心を通る直線は反転で不変でありまた、接したり交わったりするなども不変であるので上で言及した2n本の直線に反転で対応する図形は一点で交わる。

無限個の族[編集]

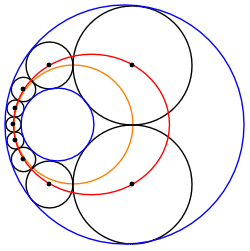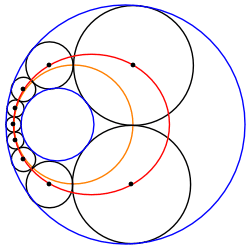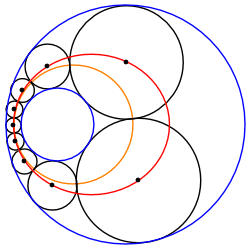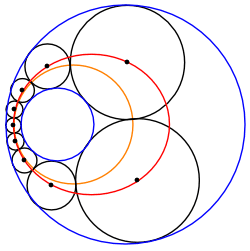
2つの円(青)について、1つでも閉じている円鎖が存在すれば、そのような円鎖は無限に存在する。

2つの交わらない円について、そのシュタイナーの円鎖を反転させたものをアニュラス上で"転がす"ことにより、別のシュタイナーの円鎖を作ることができる。故に、2つの与円についてのシュタイナーの円鎖は無限個ある。

中心の軌跡[編集]

シュタイナー円鎖を成す円の中心は常に二次曲線上にある。例えば元の円の一方の円がもう一方の円の内部にある場合は楕円、外部にある場合は双曲線となる。これはアポロニウスの問題やパップス円鎖にも利用されている。3次元ではソディの六球連鎖に応用されている。

元の2円を $α,β$ 、その半径をそれぞれ $r α,r β$ 、中心をそれぞれ $A,B$ とする。ただし $α$ は $β$ の内部にあるとする。またシュタイナーの円鎖の $k$ 番目の円の円周、半径、直径、中心をそれぞれ $C k,r k,d β,P k$ とする。

$P k$ は常にある楕円上にある。これは円が接することを式にしたとき下記の様になり、この時 $P k$ の軌跡はよく知られた事実により楕円となるためである。

{\overline {\mathbf {P} _{k}\mathbf {A} }}+{\overline {\mathbf {P} _{k}\mathbf {B} }}=(r_{\alpha }-r_{k})+\left(r_{\beta }+r_{k}\right)=r_{\alpha }+r_{\beta }

このため $P k$ とそれぞれ $A,B$ の距離の和は常に $r α + r β$ となる。特に、この楕円の焦点は $A,B$ となることが従う。

更にこの楕円の長軸 $a$ は以下の式を満たす。

2a=r_{\alpha }+r_{\beta }

$p$ を $A,B$ の距離とすると、楕円の離心率 $e$ について以下の式が成立する。

e={\frac {p}{2a}}={\frac {p}{r_{\alpha }+r_{\beta }}}

短軸を $b$ 、半直弦を $L$ とすれば以下の式が成り立つ。

b^{2}=a^{2}\left(1-e^{2}\right)=a^{2}-{\frac {p^{2}}{4}}

L={\frac {b^{2}}{a}}=a-{\frac {p^{2}}{4a}}

したがって軌道の方程式は以下のようになる。

d={\frac {L}{1-e\cos \theta }}

ここで $θ$ は軌跡を成す点が二つの頂点に対して成す角である。

円鎖の共役[編集]

n=4での円鎖の共役
赤と青の円に対する4円でのシュタイナーの円鎖
左図と同じではあるが最初の円を変えたもの
左図と同じではあるが最初の円を変えたもの

シュタイナーの円鎖は偶数個の円で構成されるならば、同じ図形内で元の2円を円鎖の正反対の円に変えても、他の円で円鎖が起きているとみなすことができる。元の円鎖が $n$ 個で $m$ 周期、初めの円を変えた後の円鎖が $p$ 個で $q$ 周期とすれば、以下の式が成り立つ。

{\frac {m}{n}}+{\frac {p}{q}}={\frac {1}{2}}.

もっとも簡単なものは円鎖が4円で構成されていて周期が1の時である。より一般的には、シュタイナーの円鎖を成す円はすべて4円と接して、与円2つはn個の円と接しているが、この場合は与円2つと、円鎖を成す4円は、すべて4つの円と接していることになる。したがって $m = q =1, n = q =4$ なので下記の様に式が成立していることが分かる。

{\frac {1}{4}}+{\frac {1}{4}}={\frac {1}{2}}.

一般化[編集]

シュタイナーの円鎖の自然な一般化は、与円が交わっているときである。一点で交わる、つまり接しているときはパップス円鎖となる。パップス円鎖は無限個の円から成る。

ソディの六球連鎖は6円のシュタイナーの円鎖を3次元に一般化した場合である。このとき六球の中心は同一円錐曲線、特に楕円上にある。六球の中心をある平面に固定したとき、六球連鎖の包絡線はデュパンのサイクライド（英語版）と呼ばれる図形となり、その反転はトーラスとなる。六球は与円にそれぞれ内接、外接するだけでなく他のある二球にも接している。

階層的に、シュタイナーの円鎖は別の一般化をすることができる。普通のシュタイナーの円鎖の2円が入れ子になっている、すなわち一方の円がもう一方の円に完全に収まっている場合、シュタイナーの円鎖は大きい方の与円に内接することになる。階層的なシュタイナーの円鎖ではシュタイナーの円鎖のそれぞれの円はそれ自身が他のシュタイナーの円鎖の円に内接している。この過程を続けていくと、アポロニウスのギャスケットのようなフラクタルを作ることができる。

出典[編集]

^ 海野啓明 (2015). “『美しい幾何学』書評：マオール，ヨスト共著，高木監訳，稲葉・河崎・田中・平澤・吉田訳”. 形の科学会誌 (形の科学会) 2 (30): 115. https://dl.ndl.go.jp/pid/13719886.
^ 修一, 森継「シュタイナー環におけるデカルトの円定理の拡張について : Extended Abstract」『数理解析研究所講究録』第1843号、2013年7月、155–162頁。
^ “シュタイナーの円環における半径の間の公式”. 2024年7月6日閲覧。
^ 平田浩一,四宮雅士 (2019-4). “池田の定理の拡張について”. 愛媛大学教育学部紀要 65巻: 137-141.
^ 平田浩一 (2014-9). “池田の定理の一般化と重心の役割について”. 日本数学教育学会高専・大学部会論文誌 25巻.
^ “アルベロス図形と算額図形の数理”. izumi-math. 2024年7月6日閲覧。
^ “円環の諸定理”. aozoragakuen.sakura.ne.jp. 2024年7月6日閲覧。

^ つまり見つかった任意のシュタイナーの円鎖の円は、元のシュタイナー鎖の円と同様に内接または外接するということ。

論文[編集]

Ogilvy, C. S. (1990). Excursions in Geometry. Dover. pp. 51–54. ISBN 0-486-26530-7
Coxeter, H.S.M.; Greitzer, S.L. (1967). Geometry Revisited. New Mathematical Library. 19. Washington: MAA. pp. 123–126, 175–176, 180. ISBN 978-0-88385-619-2. Zbl 0166.16402
Johnson RA (1960). Advanced Euclidean Geometry: An elementary treatise on the geometry of the triangle and the circle (reprint of 1929 edition by Houghton Mifflin ed.). New York: Dover Publications. pp. 113–115. ISBN 978-0-486-46237-0
Wells D (1991). The Penguin Dictionary of Curious and Interesting Geometry. New York: Penguin Books. pp. 244–245. ISBN 0-14-011813-6

参考文献[編集]

Eves H (1972). A Survey of Geometry (revised ed.). Boston: Allyn and Bacon. pp. 134–135. ISBN 978-0-205-03226-6
Pedoe D (1970). A Course of Geometry for Colleges and Universities. Cambridge University Press. pp. 97–101. ISBN 978-0-521-07638-8
Coolidge JL (1916). A Treatise on the Circle and the Sphere. Oxford: Clarendon Press. pp. 31–37

外部リンク[編集]

Weisstein, Eric W. "Steiner Chain". mathworld.wolfram.com (英語).
Interactive animation of a Steiner chain, CodePen
nteractive Applet by Michael Borcherds showing an animation of Steiner's Chain with a variable number of circles made with GeoGebra.

[1] 海野啓明 (2015). “『美しい幾何学』書評：マオール，ヨスト共著，高木監訳，稲葉・河崎・田中・平澤・吉田訳”. 形の科学会誌 (形の科学会) 2 (30): 115. https://dl.ndl.go.jp/pid/13719886.

[2] 修一, 森継「シュタイナー環におけるデカルトの円定理の拡張について : Extended Abstract」『数理解析研究所講究録』第1843号、2013年7月、155–162頁。

[3] “シュタイナーの円環における半径の間の公式”. 2024年7月6日閲覧。

[4] 平田浩一,四宮雅士 (2019-4). “池田の定理の拡張について”. 愛媛大学教育学部紀要 65巻: 137-141.

[5] 平田浩一 (2014-9). “池田の定理の一般化と重心の役割について”. 日本数学教育学会高専・大学部会論文誌 25巻.

[6] “アルベロス図形と算額図形の数理”. izumi-math. 2024年7月6日閲覧。

[7] “円環の諸定理”. aozoragakuen.sakura.ne.jp. 2024年7月6日閲覧。

[8] つまり見つかった任意のシュタイナーの円鎖の円は、元のシュタイナー鎖の円と同様に内接または外接するということ。

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[注釈 1]