モジュラー群

数学においてモジュラー群(modular group)とは、数論、幾何学、代数学や他の現代の数学の分野における基礎研究対象であり、幾何学的変換群や行列群により表されるものである。

定義

モジュラー群 $\Gamma$ は、ad − bc = 1 を満たす整数 a, b, c, dによって、

$z\mapsto {\frac {az+b}{cz+d}}$

と表せる複素上半平面の一次分数変換の群である。群演算は写像の合成である。

この変換の群は、特殊射影線型群 PSL(2, Z) に同型である。PSL(2, Z)は整数上の 2-次元の特殊線型群 SL(2, Z) をその群の中心 {I, −I} で割った商である。言い換えると、PSL(2, Z) は、 ad − bc = 1 を満たす整数a, b, c, dによって

${\begin{pmatrix}a&b\\c&d\end{pmatrix}}$

と表される全ての行列で構成される。ただし、行列 A と -A は同一視する。群の演算は通常の行列の積である。

モジュラー群を PSL(2, Z) であると定義する著者がいる一方で、より大きな群である SL(2, Z) であると定義する者もいる。

数学的な関係より、+1または-1の行列式をもつ行列の群 GL(2, Z) を考えることを求めることもある。（ SL(2, Z) はこの群の部分群である。）同様に、PGL(2, Z) は商群 GL(2,Z)/{I, −I} である。単位行列式を持つ 2 × 2 行列は、シンプレクティック行列であるので、SL(2, Z) = Sp(2, Z) は 2 × 2 行列のなすシンプレクティック群である。

数論的性質

${\begin{pmatrix}a&b\\c&d\end{pmatrix}}$

の行列式が１であるということは、分数 a/b, a/c, c/d, b/d がすべて既約であること、つまり、共通因子を持たないこと（もちろん分母が 0 ではないという条件で）を意味する。もっと一般的には、p/q が既約分数であれば、

${\frac {ap+bq}{cp+dq}}$

も既約となる（繰り返すが、分母は 0 ではないという条件で）。既約分数の任意のペアは、このように関連つけることができる。つまり、任意の既約分数のペア p/q と r/s に対して、

$r=ap+bq$　と　$s=cp+dq$

となるような

${\begin{pmatrix}a&b\\c&d\end{pmatrix}}\in \operatorname {SL} (2,\mathbf {Z} )$

が存在する。

モジュラー群の元は、2次元の周期格子上の対称性をもたらす。$\omega _{1}$ と $\omega _{2}$ を 2つの比率が実数でないような 2つの複素数とすると、点の集合

$\Lambda (\omega _{1},\omega _{2})=\{m\omega _{1}+n\omega _{2}:m,n\in \mathbf {Z} \}$

は、平面上の平行四辺形の格子となる。異なるベクトルのペア $\alpha _{1}$ と $\alpha _{2}$ が全く同じ格子を生成することと、$\operatorname {SL} (2,\mathbf {Z} )$の行列を用いて

${\begin{pmatrix}\alpha _{1}\\\alpha _{2}\end{pmatrix}}={\begin{pmatrix}a&b\\c&d\end{pmatrix}}{\begin{pmatrix}\omega _{1}\\\omega _{2}\end{pmatrix}}$

と書けることは等価である。このため、楕円函数のような二重周期函数(doubly periodic function)は、モジュラー群対称性を持つ。

有理数に対するモジュラー群の作用は、格子点 (p, q) が分数 p/q を表している正方格子として可視化すると、最も容易に理解することができる（ユークリッドのオーチャード(Euclid's orchard)を参照のこと）。この格子においては、既約分数は原点から見ることのできる点である。分数上のモジュラー群の作用は、見ることのできる点を見ることができない（既約な）点へ変換することは決してないし、逆も成り立つ。

$p_{n-1}/q_{n-1}$ と $p_{n}/q_{n}$ が 連続した２つの連分数の近似分数あれば、行列

${\begin{pmatrix}p_{n-1}&p_{n}\\q_{n-1}&q_{n}\end{pmatrix}}$

は GL(2, Z) に属する。特に、a < b かつ c < d である正の整数 a, b, c, d に対し、bc − ad = 1 であれば、a/b と c/d は max(b, d) に対応するファレイ数列において隣接する。連分数の近似分数の特別に重要な例として、フィボナッチ数列とペル方程式の解がある。どちらの場合も、モジュラー群の半群を形成するように数列を並べることができる。

群論的な性質

表示

モジュラー群は、次の 2つの変換

$S:z\mapsto -1/z$

$T:z\mapsto z+1$

により生成されると見ることができ、すべてのモジュラー群の元は、S と T の（一意ではない）合成により表すことができる。幾何学的には、S は単位円に関する反転をしてから虚軸に対して線対称の位置への移動を表し、T は右方向への１単位の移動を表す。

生成元 S と T は関係式 S² = 1 と (ST)³ = 1 を満たす。 これらは関係式の完全な集合であることが示されており、よって、モジュラー群は次の表示(presentation)を取る。

$\Gamma \cong \langle S,T\mid S^{2}=I,(ST)^{3}=I\rangle$

この表示は、回転する三角形群(triangle group) (2,3,∞) （∞ は T 上の関係式が存在しない）としてモジュラー群を記述する。また、関係式 Tⁿ = 1 を加えることにより、三角形群 (2,3,n) 全体の上へ写像する。たとえば、これは合同部分群 Γ(n) を発生させる。

生成元 S と ST を S と T の代わりに使うと、このことからモジュラー群は巡回群 C₂ と C₃ の自由積(free product)に同型である。すなわち、

$\Gamma \cong C_{2}*C_{3}\ .$

ブレイド群

ブレイド群 B₃ は、モジュラー群の普遍中心拡大(universal central extension)である。

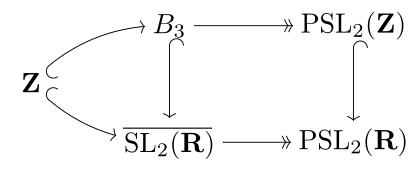
ブレイド群 B₃ は、（位相的）普遍被覆群 ${\overline {\mathrm {SL} _{2}(\mathbf {R} )}}\to \mathrm {PSL} _{2}(\mathbf {R} )$ の中の格子としてこれらを置いたモジュラー群の普遍中心拡大である。さらに、モジュラー群は自明な中心を持っているので、B₃ の中心を modulo とする商群と同型である。同じことであるが、B₃ の内部自己同型(inner automorphism)の群に同型である。

ブレイド群 B₃ は三葉結び目の結び目群 である。

双曲幾何学との関係

「PSL2(R)」も参照

モジュラー群は、双曲平面の等長(isometries)群の部分群をなすので、重要である。双曲平面の幾何学の上半平面モデル H を考えると、H のすべての向きを保つ(orientation-preserving)等長群は、a, b, c, d を普通の実数の代わりに整数とし、ad − bc = 1 とすると、

$z\mapsto {\frac {az+b}{cz+d}}$

形のメビウス変換のすべてから構成される。また、これとは別に次の式に従う H 上の PSL(2, R) 群の作用でもある。

${\begin{pmatrix}a&b\\c&d\end{pmatrix}}\cdot z\,=\,{\frac {az+b}{cz+d}}\ .$

この（左-）作用は、忠実であり、PSL(2, Z) は PSL(2, R) の部分群であるので、モジュラー群は H の向きを保つ等長群の部分群である。

双曲平面のタイル貼り

上半平面上の Γ の作用の典型的な基本領域

モジュラー群 Γ は H 上に PSL(2, R) の離散部分群(discrete subgroup)として作用する、つまり、H の各々の 元 z に対して、z の近傍をとり、z の軌道の他の元を含まないようにすることができる。このことはまた、基本領域を構成することができることを意味する。（大まかには、）基本領域は H の中のすべての z の軌道からちょうど一つづつの代表元を選ぶことで構成することができる。（領域の境界に注意が必要である。）

基本領域を構成する方法は多数あるが、すべてに共通なことは、領域

$R=\left\{z\in \mathbf {H} :\left|z\right|>1,\,\left|\,{\mbox{Re}}(z)\,\right|<{\frac {1}{2}}\right\}$

は、垂直線 Re(z) = 1/2 と Re(z) = −1/2 と円 |z| = 1 により囲まれていることであり、双曲三角形である。また、頂点 1/2 + i√3/2 と −1/2 + i√3/2 を持ち、辺どうしのなす角度が π/3 であり、三番目の頂点が無限点では、辺どうしのなす角度が 0 である。 この領域をモジュラー群の各々の元で変換すると、合同双曲三角形により双曲平面のタイリングが作られる。そのような三角形は無限点か、または実軸 Im(x) = 0 上のどちらかに一つの頂点を持つことに注意する。このタイリングはポアンカレ円板の拡張であり、そこではすべての双曲三角形が円板の境界に一つの頂点を持つ。ポアンカレ円板のタイリングは、モジュラー群の下に不変であるJ-不変量により自然な方法で与えられ、すべての複素数にこれらの領域の各々の三角形の中のひとつの点が与えられる。

このタイリングは、各々の領域を半分づつに分割（黒色と白色と塗り分けて）し、反対の向きを加えることで、少し改善することができる。(x, y) ↦ (−x, y) と変換し、領域 R (Re(z) ≥ 0) の右半分をとることは、通常のタイリングをとることである。まず、このタイリングは(Klein & 1878/79a),で提示され、このことはリヒャルト・デデキント(Richard Dedekind)による(Dedekind 1877) を参照した。

付帯するタイリンクを写像することにより、写像 (2, 3, ∞) → (2, 3, 7) を可視化

（モジュラー群から三角形群への）写像 (2, 3, ∞) → (2, 3, n) の群は、このタイリングのことばで（モジュラー曲線のタイリングである）右図のように可視化することができる。

合同部分群

詳細は「合同部分群」を参照

モジュラー群 Γ の重要な部分群には、合同部分群(congruence subgroup)と呼ばれる群があり、付帯する行列の上に合同関係式を導入することにより与えられる。

自然な準同型 SL(2, Z) → SL(2, Z/NZ) が各要素に対して modulo N をとることにより得られる。このことはモジュラー群の準同型 PSL(2, Z) → PSL(2, Z/NZ) を導く。この準同型の核は、レベル N の主合同部分群(principal congruence subgroup)と呼ばれ、Γ(N) と書く。次の短完全系列を得る。

$1\to \Gamma (N)\to \Gamma \to {\mbox{PSL}}(2,\mathbf {Z} /N\mathbf {Z} )\to 1$.

準同型の核 Γ(N) はモジュラー群 Γ の正規部分群である。群 Γ(N) は、a ≡ d ≡ ±1 (mod N) であり b ≡ c ≡ 0 (mod N) であるすべてのモジュラー変換

$z\mapsto {\frac {az+b}{cz+d}}$

の集合である。

レベル 2 の主合同部分群 Γ(2) はモジュラー群 Λと呼ばれる。PSL(2, Z/2Z) は対称群 S₃ と同型であるので、Λ は指数 6 の部分群である。群 Λ は、a と d が奇数で、b と d が偶数であるすべてのモジュラー変換からなる。

他の重要な合同部分群の族に、モジュラー群ガンマ0(modular group Γ₀(N))が c ≡ 0 (mod N)、同じことであるが、N を modulo として上三角変換のすべてのモジュラー変換の集合として定義される。Γ(N) は Γ₀(N) の部分群である。これらの群に付帯するモジュラー曲線は、モンストラス・ムーンシャインの一側面でもある。ある素数 p に対し、正規化されたモジュラー曲線の種数が 0 であることと、p がモンスター群の位数を割ることとは同値である。同じことであるが、p が超特異素数(supersingular prime)とは同値である。

写像トーラス

群 GL(2, Z) は、標準格子 Z² を保存する線形写像であり、SL(2, Z) はこの格子の向きを保存する写像である。これらは、（SL 写像は向きを保存する）トーラスの半同相(self-homeomorphism)となり、実際、トーラスの（拡張された）写像類群(mapping class group)に同型な写像は、トーラスのすべての半同相写像は、この形の写像と等方的(isotopic)となる。GL(2, Z) の元としての代数的性質はトーラスの誘導写像の力学と対応する。

ヘッケ群

モジュラー群は、エーリッヒ・ヘッケの名前をとったヘッケ群へ一般することができ、次のように定義することができる

ヘッケ群 H_q は離散群で、$\lambda _{q}=2\cos(\pi /q)$ とすると、

$z\mapsto -1/z$

$z\mapsto z+\lambda _{q},$

により生成される。

モジュラー群 Γ は H₃ に同型であり、性質や応用を共有する。たとえば、巡回群の自由積(free product)である

$\Gamma \cong C_{2}*C_{3},$

や、より一般的には、三角形群(triangle group) (2, q, ∞) に対応する

$H_{q}\cong C_{2}*C_{q},$

を持っている。Z[λ] の主イデアルに付帯する主合同部分群の考え方も存在する。小さな値の q に対し、

$\lambda _{3}=1,$

$\lambda _{4}={\sqrt {2}},$

$\lambda _{5}={\tfrac {1}{2}}(1+{\sqrt {5}}),$

$\lambda _{6}={\sqrt {3}}$

である。

歴史

モジュラー群とその部分群は、最初に、詳細にリヒャルト・デーデキント (Richard Dedekind) とフェリックス・クライン (Felix Klein) により、1870年代に彼らのエルランゲン・プログラムの一部として研究された。しかし、密接に関連する楕円曲線は、1785年にジョゼフ＝ルイ・ラグランジュ(Joseph Louis Lagrange)により研究され、さらに楕円函数に関する結果は、カール・グスタフ・ヤコブ・ヤコビ(Carl Gustav Jakob Jacobi)とニールス・アーベル(Niels Henrik Abel)により1827年に出版された。

関連項目

• メビウス変換
• フックス群(Fuchsian group)
• ビアンキ群
• クライン群(Kleinian group)
• 双曲タイリング(Hyperbolic tiling)
• モジュラー函数
• J-不変量
• モジュラー形式
• モジュラー曲線
• 古典的モジュラー曲線(classical modular curve)
• ポアンカレの上半平面モデル
• ミンコフスキーの疑問符関数(Minkowski question-mark function)
• 写像類群(Mapping class group)

参考文献

• Tom M. Apostol, Modular Functions and Dirichlet Series in Number Theory, Second Edition (1990), Springer, New York ISBN 0-387-97127-0 See chapter 2.
• Klein, Felix (1878/79), “Über die Transformation der elliptischen Funktionen und die Auflösung der Gleichungen fünften Grades (On the transformation of elliptic functions and ...)”, Math. Annalen 14: 13–75 (in Oeuvres, Tome 3), http://mathdoc.emath.fr/cgi-bin/oetoc?id=OE_KLEIN__3 
• Dedekind, Richard (September 1877), “Schreiben an Herrn Borchard uber die Theorie der elliptische Modulfunktionen”, Crelle's Journal 83: 265–292 .