ヒッグス機構
| 標準模型 | ||||||||
|---|---|---|---|---|---|---|---|---|
| ||||||||
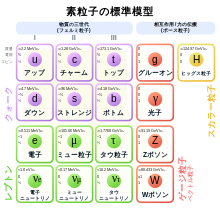
| 標準模型の素粒子 | ||||||||
| ||||||||
ヒッグス機構(ヒッグスきこう、Higgs mechanism)とは、ピーター・ヒッグスが1964年に提唱した、ゲージ対称性の自発的破れとゲージ粒子の質量獲得に関する理論である[1]。
ゲージ理論においてゲージ場が質量項を持つことはないが、ヒッグス機構ではヒッグス場が真空期待値を持つことで系の対称性を破り、ゲージ粒子はヒッグス場との相互作用を通して質量を獲得するものと考える。
ただし、この理論によれば真空と同じ量子数を持つスカラー粒子が現れるとされるので、この理論が現実の物理に適用できるものだと証明するためには、その粒子(ヒッグス粒子)を実験的に見つけることが課題になる[2]。
この機構(メカニズム)は、まず1962年にフィリップ・アンダーソンによって提唱され、類似のモデルが1964年に3つの独立したグループによって発展させられた。すなわち (1) ロベール・ブルーen:Robert Broutとフランソワ・アングレール 、(2) ピーター・ヒッグス、および(3) en:Gerald GuralnikとC. R. HagenとTom Kibbleの3グループである。よって、このメカニズムは次のような様々な呼称で呼ばれている。Brout–Englert–Higgs mechanism(ブルー・エングレール・ヒッグス・メカニズム)、あるいはEnglert–Brout–Higgs–Guralnik–Hagen–Kibble mechanism,[3] Anderson–Higgs mechanism,[4] Higgs–Kibble mechanism(アブドゥッサラームによる)[5]あるいはできるだけ頭文字だけにしてABEGHHK'tH mechanism (Anderson, Brout, Englert, Guralnik, Hagen, Higgs, Kibble and 't Hooftの頭文字。ピーター・ヒッグスが他の研究者たちに敬意を払ってこう呼んだ。)[5]。
概要[編集]
ゲージ対称性を持つ理論において、ラグランジアンの中にゲージ場の質量項は入らないため、ゲージ場の裸の質量は0である。しかしながら、ヒッグス機構はゲージ場とスカラー場の相互作用によって、低エネルギーにおいてゲージ粒子に質量を与えることが出来る[2]。 つまり、もしヒッグス機構が起こっていれば、従来は困難とされたゲージ粒子の質量に対して、物理学的に整合性を保った、合理的な説明が与えられる。
系の対称性が破れると南部・ゴールドストーン粒子が生じるが、この機構が起こるときには物理的な南部・ゴールドストーン粒子は現れず、その自由度はゲージ場の縦波成分として吸収されてゲージ場は質量を持ったベクトル粒子となる[2]。 この機構において系の対称性を破るために導入される場はヒッグス場と呼ばれる[6]。 ヒッグス場はゲージ群の下で非自明な表現(チャージ)をもち、ゲージ理論に従ってゲージ相互作用をする。 ヒッグス場が真空期待値をもつと対称性が破れ、ヒッグス場とのゲージ相互作用を通じてゲージ場は質量を獲得する。 対称性が破れた後に残る場が量子化されて得られる粒子がヒッグス粒子である[6]。
標準模型における例[編集]
ワインバーグ=サラム理論或いはそれを含む標準模型において、ヒッグス場はウィークアイソスピンとウィークハイパーチャージのチャージをもつ。 ヒッグス場が真空期待値をもつと、電弱対称性が破れてWボソンとZボソンは質量を獲得する。 なお、フェルミオンはヒッグス場が真空期待値を持つことで湯川相互作用を通して質量を獲得するが、湯川相互作用項はゲージ理論から要請される項ではない。
簡単な例[編集]
簡単な例としてtreeレベルのU(1)ゲージ理論を考える。ラグランジアンは
である。 共変微分とゲージ場の強度は
である。
ポテンシャル項からヒッグス場の真空期待値は
であるが、真空期待値の位相を選んだ時点で対称性が破れる。以降は位相θ=0と選ぶ。
真空からのゆらぎを
と書いたとき、ラグランジアンは
となる。 ここで、 は
により再定義されたベクトル場である。 再定義されたベクトル場には質量項が存在し、その質量は
である。 再定義されたベクトル場の強度は
である。 は再定義されたベクトル場に吸収されてラグランジアンに出てこない。 残ったスカラー場 の質量は
である。このスカラー場 がヒッグスボソンである。 ヒッグス機構により生じる質量は、ヒッグス場の真空期待値の大きさに比例し、その比例係数はヒッグス場との相互作用の結合定数により決まる。
ゲージ場 への再定義は元のゲージ場 にゲージ固定を施すことと等価であり、当然ゲージ変換によって が現れるラグランジアンを構成することも可能であるが、ゲージ変換によって消滅する場である は物理的な自由度を有しない。このように自発的対称性の破れによって現れる無質量のボゾン場を南部=ゴールドストーンボゾンと呼ぶ。対して物理的な自由度を有する は物理的なヒッグス粒子を記述し、 の質量項や相互作用項によって物理的なヒッグス粒子の質量、相互作用が記述される。 南部=ゴールドストーンボゾンがラグランジアンに現れないゲージ固定をユニタリティゲージ呼び、このゲージ固定の下ではゲージ場のプロパゲータは
と書かれる。ユニタリティゲージの下では場の自由度が少なくラグランジアンに現れる相互作用も少なくて済むが上記の通りプロパゲータの形が複雑になり摂動計算には不向きである[7]。 トフーフト=ファインマンゲージなど摂動計算に便利なゲージ固定の下では南部=ゴールドストーンボゾンとの相互作用が現れるが、その際南部=ゴールドストーンボゾンのプロパゲータは質量 を持つ形で書かれる。 これはゲージ場 の縦波成分と南部=ゴールドストーンボゾンが等価である(Equivarence Theorem)ことに由来する。
脚注[編集]
- ^ Higgs (1964)
- ^ a b c 『改訂 物理学事典』 p.1710 「ヒグス機構」
- ^ “Englert–Brout–Higgs–Guralnik–Hagen–Kibble Mechanism on Scholarpedia”. Scholarpedia.org. 2012年6月16日閲覧。
- ^ Liu, Guo-Zhu; Cheng, Geng (2002). “Extension of the Anderson-Higgs mechanism”. Physical Review B 65 (13). doi:10.1103/PhysRevB.65.132513. ISSN 0163-1829.
- ^ a b Close, Frank (2011). The Infinity Puzzle: Quantum Field Theory and the Hunt for an Orderly Universe. Oxford: Oxford University Press. ISBN 978-0-19-959350-7
- ^ a b 標準模型(電弱対称性)のもののみを指して使われる場合もあるが、通常は大統一論に現れる大きなゲージ群を破る場や標準模型の拡張版のヒッグス場など自発的に対称性を破るスカラー場一般をヒッグス場と呼ぶ。
- ^ 九後 (1989) (「摂動計算に不向き」は原文ままである)
参考文献[編集]
- 論文
-
- P. W. Higgs (1964). “Broken symmetries, massless particles and gauge fields”. Phys. Lett. 12: 132.
- 参考書籍
-
- 九後汰一郎『ゲージ場の量子論Ⅱ』培風館〈新物理学シリーズ〉、1989年。ISBN 4-563-02424-4。
- 『改訂 物理学事典』培風館、1992年。
















