アムダールの法則
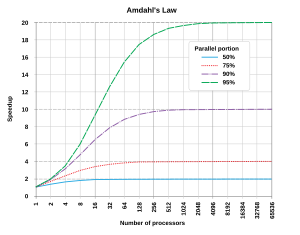
アムダールの法則(アムダールのほうそく、英語: Amdahl's law)は、ある計算機システムとその対象とする計算についてのモデルにおいて、その計算機の並列度を上げた場合に、並列化できない部分の存在、特にその割合が「ボトルネック」となることを示した法則である。コンピュータ・アーキテクトのジーン・アムダールが主張したものであり、アムダールの主張(アムダールのしゅちょう、英語: Amdahl's argument)という呼称もある[1]。
複数のプロセッサを使い並列計算によってプログラムの高速化を図る場合、そのプログラムの中で逐次的に実行しなければならない部分の時間によって、高速化が制限される。例えば、1プロセッサでは20時間かかる問題があり、そのプログラムのうち、合計で1時間分が並列処理できないとする。この場合、19時間分(95%)は並列処理できるが、どれだけプロセッサを追加したとしても、最小実行時間は並列処理できない部分にかかる1時間(5%)より短くならない。
詳細[編集]
アムダールの法則は、並列化しても問題の大きさが変化しないという前提と、問題には並列化できない部分があるという前提の上で、逐次的アルゴリズムとそれに対応したアルゴリズムの並列化実装によって期待できる高速化の関係をモデル化したものである。例えば、ある大きさの問題をあるアルゴリズムを並列化実装したもので実行した場合、問題の12%を並列化によって好きなように高速化できるとする(残り88%は並列化できない処理である)。アムダールの法則によれば、このときの並列化していない実装と比較した並列化版による高速化は最大でも 倍にしかならない。
より技術的に解説すると、この法則は、ある計算のうち高速化によって影響を受ける部分の割合 P とその性能向上率 S から、全体として達成可能な性能向上率を求めるものである。例えば、ある改良が計算全体の 30% に影響する場合、P は 0.3 である。また、その部分が2倍に高速化されるなら S は 2 である。アムダールの法則によれば、全体としての性能向上は次の式で表される。
- .
従来の計算時間を 1 とする。改良されたプログラムの計算時間は、改良と関係しない部分の計算時間(1 − P)と改良された部分の計算時間(P/S)の合計となる。全体の性能向上率は、従来の計算時間を改良されたプログラムの計算時間で割ったものであり、上の式はそれを表している。
もう少し複雑な例を挙げる。あるタスクが4つの部分に分割されるとする。各部のタスク実行時間に占める割合は P1 = 0.11 (11%)、P2 = 0.18 (18%)、P3 = 0.23 (23%)、P4 = 0.48 (48%) で、全部を合計すると 100% になる。そこで、各部分に独自の改良を施す。P1 は改良しないので S1 = 1 (100%)、P2 は5倍に性能向上したので S2 = 5 (500%)、同様に S3 = 20 (2000%)、S4 = 1.6 (160%) とする。改良されたタスクの実行時間は であるから、これに代入すると
となり、オリジナルの半分弱の時間ということがわかる。従って、性能向上率は と約2倍以上になる。注意すべきは、20倍とか5倍といった改良を施しても、システム全体としてはあまり効果が出ない点である。これは、P4 が元々実行時間の約半分を占めていて、S4 が 1.6 という点と P1 が全く改良されていない点が影響している。
並列化[編集]

プログラムの並列化できる部分の実行時間の割合を P としたとき、並列化不可能な部分は (1 − P)であり、N個のプロセッサを使ったときの全体の性能向上率は次の式で表される。
N が無限大に近づく極限では、性能向上率は 1 / (1 − P) となる。実際、(1 − P) の並列化不可能な成分がどれほど小さくとも N が大きくなれば価格性能比は急激に低下していく。
例として、P が90%ならば (1 − P) は 10% となり、N をどれだけ大きくしても性能向上は1プロセッサの10倍までで頭打ちとなる。このため、並列計算が有効であるのは、プロセッサ数が少ない場合か、適応領域の問題の P の値が極めて大きい場合(embarrassingly parallel 問題と呼ぶ)に限られる。並列計算のプログラミング技法の多くは、(1 – P) を可能な限り小さくするためのものである。
特定のプロセッサ数 (NP) での実測高速化係数 (SU) すなわち1プロセッサの何倍の性能かという値を使えば、P すなわち並列化可能部分の割合は次のように推定できる。
このように推定した P をアムダールの法則の式に適用すれば、異なるプロセッサ数での高速化の度合いが推定できる。
| プロセッサ数(N) | 順次実行部分の実行時間の割合 |
|---|---|
| 2 | 25% |
| 4 | 8.3% |
| 6 | 5.0% |
| 8 | 3.6% |
| 12 | 2.3% |
| 16 | 1.7% |
| 32 | 0.81% |
| 64 | 0.40% |
| 256 | 0.10% |
| 1024 | 0.024% |
| 4096 | 0.0061% |
| 65536 | 0.00038% |
これは 0.25 / (N - 1) で計算できる。
収穫逓減の法則との関係[編集]
アムダールの法則は収穫逓減の法則と組み合わせて述べられることが多いが、アムダールの法則を適用した特殊な例のみが「収穫逓減の法則」を示す。最初から(性能向上の観点で)最適な実装をしていく場合、改良に対して得られる性能向上は単調減少していく。しかし最適でない改良なら、さらなる改良を施すことで新たな性能向上が得られる場合もある。一般にシステムの改良は困難を伴う場合や時間がかかる場合があり、必ずしも常に最善の改良を行えるわけではない。
プロセッサを追加するとそれに対応して並列化して動作するプログラムがあるとする。そのようなプログラムで解くべき問題の大きさが固定の場合に、プロセッサを追加して性能向上を図ろうとしたとき、アムダールの法則は収穫逓減の法則と同じことを表す。プロセッサを追加する度に、それによって得られる性能向上の度合いは減っていく。プロセッサを倍増させたときの性能向上比率は減少していき、最終的には へと近づいていく。
ここでは、メモリ帯域幅やI/O帯域幅といったボトルネックの可能性を考慮していない。それらがプロセッサ数に比例して拡大しないなら、収穫逓減の傾向がさらに強まることになる。
アムダール本人の見解[編集]
結局のところ(並列化のオーバヘッドといったものを全て無視できるとしても)、解きたい問題が必要とする計算のうち、どれだけが並列化可能か、という点が支配的であり、アムダール本人は並列化による高性能化に悲観的であったと言われる[2]。高性能計算の識者の間でも以前は見解が分かれており、ゴードン・ベル賞はこの問題へのチャレンジとして当初は設定された[3]。
逐次的プログラムの高速化[編集]

ある逐次的プログラムを改良したときの最大高速化係数は、そのプログラムの一部を 倍に高速化した場合、次の不等式で表される。
ここで () は、改良した部分の(改良以前の)所要時間の割合である。例えば(右図参照)、
- B を5倍に高速化した場合 ()、、、 とすると、
- A を2倍に高速化した場合 ()、、、 とすると、
となる。したがって、Aを2倍に高速化した方がBを5倍に高速化するよりもよい結果となる。性能向上をパーセントで表す場合、次のように計算できる。
- Aを2倍に高速化すると、プログラム全体は1.6倍に高速化し、オリジナルから37.5%の性能向上となる。
- しかし、Bを5倍に高速化しても、全体としては1.25倍の高速化でしかなく、20%しか性能向上しない。
グスタフソンの法則との関係[編集]
1988年、ジョン・グスタフソンはグスタフソンの法則と呼ばれることを指摘した。すなわち、人々が関心を持っているのは、アムダールの法則で示されるように、既に解かれた問題をより高速に解くことではなく、より大きな問題を(可能な限り正確な近似で)それなりの時間内に解くことだ、という点である。並列化できない部分が固定あるいは、問題の大きさの増大に対して非常にゆっくり増大する場合(例えば、O(log n))、解ける問題の大きさはプロセッサの追加に比例して増大していく。
関連項目[編集]
脚注[編集]
- ^ Rodgers 1985, p. 226
- ^ 富士通と共同開発したアムダールコンピュータでも、アムダール側のモデルはマルチプロセッサとしなかった( http://homepage2.nifty.com/Miwa/6_F230-60/6_7(4).html )
- ^ https://twitter.com/ProfMatsuoka/status/536447955352289280
参考文献[編集]
- Amdahl, Gene (1967). “Validity of the Single Processor Approach to Achieving Large-Scale Computing Capabilities” (PDF). AFIPS Conference Proceedings (30): 483–485.
- Rodgers, David P. (June 1985). “Improvements in multiprocessor system design”. ACM SIGARCH Computer Architecture News archive (New York, NY, USA: ACM) 13 (3): 225–231. doi:10.1145/327070.327215. ISSN 0163-5964.
外部リンク[編集]
- Cases where Amdahl's law is inapplicable
- Oral history interview with Gene M. Amdahl Charles Babbage Institute, University of Minnesota.
- Reevaluating Amdahl's Law
- Reevaluating Amdahl's Law and Gustafson's Law
- A simple interactive Amdahl's Law calculator
- "Amdahl's Law" by Joel F. Klein, Wolfram Demonstrations Project, 2007.
- Amdahl's Law in the Multicore Era
- Amdahl's Law explanation
- Blog Post: "What the $#@! is Parallelism, Anyhow?"
- Amdahl's Law applied to OS system calls on multicore CPU





















