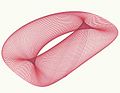
ハーモノグラフ

ハーモノグラフ(英: harmonograph)は幾何学像を生成するために振り子を用いる機械的装置。生成される図は普通はリサージュ曲線、もしくはより複雑な関連する図である。19世紀中ごろに登場し1890年代に人気のピークを迎えたこの装置は1人の人間に帰属することはできないが、グラスゴー大学の数学教授を務めていたHugh Blackburnが一般的には発明者であると考えられている[1]。
単純ないわゆる「横」ハーモノグラフは2つの振り子を用いて描く面に対するペンの動きを制御する。1つの振り子はペンを1つの軸に沿って前後に動かし、もう1つの振り子は描く面を垂直軸に沿って前後に動かす。振り子の相対的な周波数と位相を変化させることで異なるパターンが生成される。前述の単純なハーモノグラフでも楕円、渦巻、figure eightsや他のリサージュ図形を生成することができる。
より複雑なハーモノグラフも存在し、3つ以上の振り子もしくは連結した振り子(例えば振り子を別の振り子にひっかける)を用いるものや、ジンバルに取り付けて任意の方向に動けるようにした振り子に回転運動を行わせるものなどがある。
ハーモノグラフの一種であるピントグラフ(図を拡大するための装置であるパントグラフとは異なる)は2つの回転ディスクの相対的な動きに基づいている(#外部リンクに図解がある)。
ブラックバーン振り子
[編集]
ブラックバーン振り子は調和振動を説明するための装置で、これを1844年に記述したHugh Blackburnにちなんで名づけられた。これは1815年にJames Deanにより最初に議論され、同年Nathaniel Bowditchにより数学的に解析された[2]。おもりが糸からつるされ、糸はV字型の糸から垂れ下がっているので、振り子は異なる周期で2つの垂直方向に同時に振動する。結果としておもりはリサージュ曲線に似た経路をたどる。これはハーモノグラフとして知られている機械装置の仲間である[3]。
20世紀半ばの物理学の教科書にはこの種の振り子を二重振り子と呼んでいるものもある[4]。
コンピュータで生成されたハーモノグラフの図
[編集]ハーモノグラフは減衰する振り子の動きを用いて図形を作成する。減衰する振り子の動きは次の方程式で表される。
は角周波数、は位相、は振幅、は減衰係数、は時間を表す。その振り子が2つの軸に対して動くことができる(円形もしくは楕円形)場合、重ね合わせの原理により、振り子の底に1つの軸に沿ってつながれたロッドの運動は方程式
で表される。普通のハーモノグラフにはこのような方法で動く2つの振り子と、これらの振り子につながれた2つの垂直ロッドにより動かされるペンがある。したがって、ハーモノグラフの通る道はパラメトリック方程式
により記述される。適切なコンピュータプログラムはこれらの方程式をグラフに変換することでハーモノグラフ図を再現できる。各方程式に最初の方程式をもう1度適用すると、動く紙をまねることができる(下図参照)。[訳語疑問点]
ギャラリー
[編集]-
ピントグラフにより作られた図
脚注
[編集]- ^ Turner, Steven (February 1997). “Demonstrating Harmony: Some of the Many Devices Used To Produce Lissajous Curves Before the Oscilloscope”. Rittenhouse 11 (42): 41.
- ^ L.P. Pook (2011). Understanding Pendulums: A Brief Introduction. Springer.
- ^ Gregory L. Baker and James A. Blackburn (2005). The Pendulum: a case study in physics. Oxford.
- ^ Francis Sears and Mark W. Zemansky: University Physics, Third Edition, Addison-Wesley Publishing Company, 1964.
関連項目
[編集]外部リンク
[編集]- A complex harmonograph with a unique single pendulum design
- Harmonograph background, equations, and illustrations
- How to build a 3-pendulum rotary harmonograph
- Interactive JavaScript simulation of a 3-pendulum rotary harmonograph
- HTML5 Animated Harmonograph
- Virtual Harmonograph web application
- An Animated Harmonograph Model in MS Excel
- An interactive Pintograph for iOS
- Harmonographs, pintographs, and Excel models