「リミットサイクル」の版間の差分
| (同じ利用者による、間の11版が非表示) | |||
| 1行目: | 1行目: | ||
[[File:VanDerPolPhaseSpace.png|thumb|300px|[[ファン・デル・ポール振動子]]で現れる安定なリミットサイクル。内側の軌道も外側の軌道も、ある閉軌道に漸近している。]] |
|||
{{出典の明記|date=2017年8月}} |
|||
'''リミットサイクル'''とは、[[力学系]]における[[相空間]]上での[[閉軌道]]であり、時間 |
'''リミットサイクル'''(英語:limit cycle)とは、[[力学系]]における[[相空間]]上での[[閉軌道]]であり、時間 {{Mvar|t}} を[[無限大]]、またはマイナス無限大にしたとき、その閉軌道に収束する軌道が少なくとも一つ存在するものである。'''極限閉軌道'''や'''極限周期軌道'''とも呼ばれる。1881年、力学系の始祖でもある[[アンリ・ポアンカレ]]によって初めて見いだされた<ref>P. Yu & W. Lin (2016) Complex dynamics in biological systems arising from multiple limit cycle bifurcation, Journal of Biological Dynamics, 10:1, 263-285, {{doi|10.1080/17513758.2016.1166270}}</ref>。 |
||
リミットサイクルは非線形系でのみ現れる。リミットサイクルの十分近くの軌道がすべてリミットサイクルに収束するとき、'''安定'''である、または''' |
リミットサイクルは非線形系でのみ現れる。リミットサイクルの十分近くの軌道がすべてリミットサイクルに収束するとき、'''漸近安定'''である、または単に'''安定'''であるという。 |
||
安定なリミットサイクルは |
安定なリミットサイクルは、閉軌道に小さな[[摂動]]が加わっても元に戻る。物理的には、リミットサイクルは[[自励振動]]の[[数理モデル]]となる。また、相空間上の様々な初期値から出発した軌道はリミットサイクル軌道に収束し、やはり[[自励振動]]を示す。リミットサイクルを持つ例として、[[ファン・デル・ポール振動子]]がある。代数的微分方程式におけるリミットサイクル軌道の数を求める問題は、[[ヒルベルトの23の問題|ヒルベルトの第16問題]]の第二の問題として知られる。2次元相空間の場合は、[[ポアンカレ・ベンディクソンの定理]]などによってリミットサイクルの存在(または非存在)を予見できる。 |
||
リミットサイクルを持つ例として、[[ファン・デル・ポール振動子]]がある。代数的微分方程式におけるリミットサイクル軌道の数を求める問題は、[[ヒルベルトの23の問題|ヒルベルトの第16問題]]の第二の問題として知られる。2次元相空間の場合は、[[ポアンカレ・ベンディクソンの定理]](またはベンディクソンの定理)によってリミットサイクル軌道の存在(または非存在)を予見できる。 |
|||
==定義== |
|||
定義として、十分近くに別の閉軌道を持たない閉軌道をリミットサイクルとする場合もある。一方で、[[カオス理論]]におけるカオスの性質の一つとして「位相空間に無限の密度でリミットサイクルを持つ領域が存在する」という例があるように、あるリミットサイクルの十分近くに別のリミットサイクルが無数に存在することを前提とした議論も存在する。 |
|||
系の時間を {{math|''t'' ∈ '''R'''}}、状態変数を {{math|1= ''X'' = (''x''<sub>1</sub>, ''x''<sub>2</sub>,... ''x<sub>n</sub>'') ∈ '''R'''''<sup>n</sup>''}} とする。{{mvar|n}} 次元連続力学系のある解 {{math|''X''(''t'')}} が[[平衡点]]ではなく、なおかつ {{math|1= ''X''(''t'') = ''X''(''t'' + ''T'')}} を満たすような {{math|''T'' > 0}} が存在するとき、{{math|''X''(''t'')}} は'''閉軌道'''(あるいは周期軌道、周期解)と呼ばれる{{Sfn|Strogatz|2015|p=161}}。特に {{math|1= ''X''(''t'') = ''X''(''t'' + ''T'')}} を満たす最小の {{mvar|T}} を'''周期'''と呼ぶ。閉軌道となる解 {{math|''X''(''t'')}} を {{mvar|C}} で表すとする。系の[[相空間]] {{math|''x''<sub>1</sub>, ''x''<sub>2</sub>,... ''x<sub>n</sub>''}} 上で、閉軌道 {{mvar|C}} は[[単純閉曲線]]を描く{{Sfn|アリグッドほか|2012|p=149}}。 |
|||
'''リミットサイクル'''は次のように定義される。ある閉軌道 {{mvar|C}} が存在するとする。{{mvar|C}} のある[[近傍 (位相空間論)|近傍]]で任意の初期点(初期値){{math|''X''<sub>0</sub>}} を取り、{{math|''X''<sub>0</sub>}} を通る解 {{math|''ϕ'' (''t'', ''X''<sub>0</sub>)}} が {{math|''t'' → ∞}} または {{math|''t'' → −∞}} で {{math|''ϕ'' (''t'', ''X''<sub>0</sub>)}} が {{mvar|C}} に漸近するとき、{{mvar|C}} はリミットサイクルと呼ばれる{{Sfn|Strogatz|2015|p=214 訳注より}}。あるいは、 |
|||
:<math>\lim_{t \to \infty} d(\phi(t, X_0),C)=0</math> |
|||
または |
|||
:<math>\lim_{t \to -\infty} d(\phi(t, X_0),C)=0</math> |
|||
となる {{mvar|C}} と {{math|''X''<sub>0</sub> ∉ C}} が存在するとき、{{mvar|C}} はリミットサイクルと呼ばれる。ここで、{{math|''d''(''ϕ''(''t'', ''X''<sub>0</sub>), ''C'')}} は時刻 {{mvar|t}} における点 {{math|''ϕ'' (''t'', ''X''<sub>0</sub>)}} と[[集合]] {{mvar|C}} の[[距離函数|距離]]である{{Sfn|Hirsch et al.|2007|pp=229–232}}。 |
|||
リミットサイクル型の振動を示す系をリミットサイクル振動子などとも呼ぶ{{Sfn|郡・森田|2011|p=17}}。「リミット」は[[極限集合]]を意味し{{Sfn|郡・森田|2011|p=17}}、リミットサイクルは'''極限閉軌道'''<ref>{{Cite book ja-jp |title=カオスはこうして発見された |editor=ラルフ・エイブラハム、ヨシスケ・ウエダ |translator =稲垣耕作・赤松則男 |publisher=共立出版 |year=2002 |edition=初版 |isbn= 4-320-03418-X }} p. 31.</ref>や'''極限周期軌道'''{{Sfn|船越|2008|p=84}}とも呼ばれる。[[極限集合]]には {{math|''t'' → ∞}} 方向の {{mvar|ω}} 極限集合と {{math|''t'' → −∞}} 方向の {{mvar|α}} 極限集合の2つがある。極限集合を用いてリミットサイクルを定義すれば、閉軌道 {{mvar|C}} が存在し、{{math|''X''<sub>0</sub> ∉ C}} の {{mvar|ω}} 極限集合 {{math|''ω''(''X''<sub>0</sub>)}} または {{mvar|α}} 極限集合 {{math|''α''(''X''<sub>0</sub>)}} が {{mvar|C}} となるとき、{{math|''ω''(''X''<sub>0</sub>)}} または {{math|''α''(''X''<sub>0</sub>)}} はリミットサイクルと呼ばれる{{Sfn|郡・森田|2011|p=53}}。 |
|||
2次元連続力学系では、相平面上でリミットサイクルは必ず孤立した閉軌道となる。すなわち、リミットサイクルとなる閉軌道 {{mvar|C}} の近傍には他の閉軌道は存在し得ない。{{mvar|C}} 近傍の全ての軌道は、{{mvar|C}} に吸引されるように近づくか、{{mvar|C}} から反発するように遠ざかるかの2通りしかない{{Sfn|Strogatz|2015|p=214}}。周りの軌道を吸引するリミットサイクルは'''漸近安定'''あるいは単に'''安定'''であるという。安定なリミットサイクルは[[アトラクタ]]の一種である{{Sfn|郡・森田|2011|pp=17, 121}}。安定なリミットサイクルのことを'''周期アトラクタ'''ともいう<ref>{{Cite book ja-jp |author = 井庭崇・福原義久 |year= 1998年 |title = 複雑系入門―知のフロンティアへの冒険 |publisher = NTT出版 |edition=初版 |isbn = 4-87188-560-7}} p. 69.</ref>。 |
|||
周りの軌道を反発するリミットサイクルは軌道不安定あるいは単に'''不安定'''であるという{{Sfn|郡・森田|2011|pp=17, 121}}。相平面のリミットサイクルで、内側の軌道が吸引されて外側の軌道が反発するような場合、あるいは内側の軌道が反発して外側の軌道が吸引されるような場合、これらの場合のリミットサイクルは'''半安定'''であるという<ref>{{Cite book ja-jp |author= 下郷太郎・田島清灝 |title=振動学 |publisher=コロナ社 |edition=初版 |year=2002 |isbn=4-339-04045-2 |series=機械系 大学講義シリーズ11}} p. 148.</ref>{{Sfn|Strogatz|2015|p=214}}。 |
|||
==存在条件== |
|||
[[実直線]]上の1次元[[自励系|自律系]]の微分方程式系では、周期解は存在し得ない{{Sfn|Strogatz|2015|pp=32–33}}。2次元自律系あるいは1次元非自律系以上から周期解が現れるようになる{{Sfn|Hirsch et al.|2007|pp=10–11}}。また、リミットサイクルは[[非線形]]の系のみで起こる現象である。[[線形力学系|線形の系]]ではリミットサイクルは起こらない{{Sfn|Strogatz|2015|p=215}}{{Sfn|郡・森田|2011|pp=17–18}}。 |
|||
[[フロー (数学)|流れ]]に沿って相空間の体積が変化しない系を[[保存系]]と呼び、体積が零に漸近する系を[[散逸系]]と呼ぶ{{Sfn|電子情報通信学会知識ベース|2010|p=3}}。散逸系の場合にリミットサイクルが存在する{{Sfn|郡・森田|2011|p=16}}。周期軌道が散逸系で存在する場合、それらの周期軌道の大抵はリミットサイクルであると推定される{{Sfn|川上|2005|p=65}}。系が[[勾配系]]である場合も、リミットサイクルは存在しない{{Sfn|桑村|2015|p=63}}。 |
|||
以下、変数の[[時間微分]] {{Math|{{Sfrac|d|d''t''}}}} を変数の上部に · を付けて表す([[ニュートンの記法]])。もし、系を2次元自律系 |
|||
:<math>\begin{align} |
|||
\dot{x} &= f(x,\ y),\\ |
|||
\dot{y} &= g(x,\ y) |
|||
\end{align}</math> |
|||
に限定すれば、閉軌道およびリミットサイクルの有無が判別できる定理がいくつかある。[[ポアンカレ・ベンディクソンの定理]]により、平衡点を含まない[[有界]]な軌道の極限集合は閉軌道である{{Sfn|Hirsch et al.|2007|p=229}}。すなわち、このような軌道は閉軌道そのものか、存在するリミットサイクルに吸引される軌道であるかのどちらかである{{Sfn|川上|2005|p=160}}。さらに、[[ベンディクソンの否定条件]]によれば、[[単連結]]な領域 {{Mvar|Ω}} 上で |
|||
:<math>\frac{\partial f(x,\ y)}{\partial x}+\frac{\partial g(x,\ y)}{\partial y}</math> |
|||
の値が零ではなく、かつ[[符号 (数学)|符号]]が一定であれば、{{Mvar|Ω}} に完全に含まれる閉軌道は存在しない{{Sfn|ウィギンス|2013|p=27}}。また、系がリエナール方程式に相当するのであれば、[[リエナールの定理]]より原点を囲む漸近安定なリミットサイクルの存在する{{Sfn|Strogatz|2015|p=230}}。 |
|||
力学系のパラメータ([[定数係数]])が変化することによって、解に定性的な変化が起こることを[[分岐 (力学系)|分岐]]という{{Sfn|電子情報通信学会知識ベース|2010|p=12}}。リミットサイクルも分岐を経て発生する。2次元系でリミットサイクルが発生する典型的な分岐は、[[ホップ分岐]]と呼ばれる分岐である{{Sfn|Strogatz|2015|pp=285}}。ホップ分岐では、パラメータ変化によって安定な平衡点が不安定に遷移し、その周囲に安定なリミットサイクルが起こる。あるいは、安定な平衡点と不安定なリミットサイクルが不安定な平衡点に遷移する場合もある{{Sfn|ウィギンス|2013|pp=276–277}}。ホップ分岐は局所分岐の一種である。リミットサイクルが関わる大域分岐としては、[[ホモクリニック分岐]]やリミットサイクル同士が衝突する[[サドルノード分岐]]などがある{{Sfn|Strogatz|2015|pp=285–289}}。 |
|||
[[File:Limit cycle Poincare map.svg|thumb|200px|2次元系のリミットサイクルにポアンカレ写像を適用した図。局所断面上の状態点が不動点へ漸近していく様子を示す。]] |
|||
周期軌道の安定性は、[[ポアンカレ写像]]の構成や周期軌道周りの[[変分方程式]](線形化方程式)の構成から判別できる。適当な {{Math|''n'' − 1}} 次元の局所断面を取り、ポアンカレ写像を設定することで連続力学系の周期解を離散力学系の写像に置き換えることができる。写像が漸近安定な不動点を持つ場合は元の周期軌道が漸近安定である{{Sfn|ウィギンス|2013|pp=64–69}}。ポアンカレ写像は、リミットサイクルを見出したポアンカレ自身がリミットサイクルを考察するために生み出した手法である{{Sfn|電子情報通信学会知識ベース|2010|p=4}}。あるいは、周期軌道からの微小なズレを想定して周期軌道に対する変分方程式を構成することによって、[[フロケ理論]]を適用することができる。変分方程式のフロケ乗数あるいはフロケ指数から周期軌道の安定性が決定できる{{Sfn|桑村|2015|pp=53–56}}{{Sfn|郡・森田|2011|pp=116–122}}。ただし、ポアンカレ写像による方法も線形化方程式による方法も、任意の微分方程式系に適用できる解析的な一般的手法は存在しない。ポアンカレ写像であれば対称の系ごとに個別に工夫して構成する必要があり、フロケ乗数による判定であれば数値計算による手法がある{{Sfn|ウィギンス|2013|p=65}}{{Sfn|桑村|2015|p=58}}。 |
|||
==具体例== |
|||
===2次元系=== |
|||
[[File:Vector field and trajectories of a simple limit cycle.svg|thumb|300px|微分方程式系 <math>\dot{x} = x - y - x(x^2 + y^2)</math>, <math>\dot{y} = x + y - y(x^2 + y^2)</math> の[[方向場]]。原点を除く全ての軌道は回転しながら[[単位円]]の閉軌道に漸近する。]] |
|||
リミットサイクルが現れる簡単な微分方程式系の例として、 |
|||
:<math>\begin{align} |
|||
\dot{x} &= x - y - x(x^2 + y^2),\\ |
|||
\dot{y} &= x + y - y(x^2 + y^2) |
|||
\end{align}</math> |
|||
という2次元系がある{{Sfn|Strogatz|2015|p=261}}<ref name="ブラウン">{{Cite book ja-jp |author=M. ブラウン |title=微分方程式 下―その数学と応用 |translator = 一樂重雄・河原正治・河原雅子・一樂祥子 |editor=シュプリンガー・ジャパン |publisher=丸善出版 |year=2012 |isbn=978-4-621-06234-0}} pp. 211–212.</ref>。この系を[[極座標]]で表せば、 |
|||
:<math>\begin{align} |
|||
\dot{r} &= r (1 - r^2),\\ |
|||
\dot{\theta} &= 1 |
|||
\end{align}</math> |
|||
となり、動径 {{mvar|r}} と偏角 {{mvar|θ}} の振る舞いが互いに無関係に決まる単純な形となる{{Sfn|Strogatz|2015|p=216}}。{{Math|''θ''(''t'')}} の一般解は一定振動数で回転し続ける関数となる。{{Math|''r''(''t'')}} の一般解は |
|||
:<math>r(t)=\frac{r_0}{\sqrt{r_0^2+(1-r_0^2)e^{-2t}}}</math> |
|||
という関数となる。ここで、{{Math|''r''<sub>0</sub>}} は {{Math|1=''t'' = 0}} における {{Mvar|r}} の値である。よって、{{Math|''r''<sub>0</sub> ≠ 0}} であれば、{{Math|''r''(''t'')}} は {{Math|''t'' → ∞}} で {{Math|''r'' → 1}} であり、系の原点を除く全ての軌道は回転しながら[[単位円]]に近づいていくこととなる<ref name="ブラウン"/>。この結果は、明示的な一般解を必要としない簡易な安定判別によっても得られる。よって、原点を中心とする単位円がこの系の安定なリミットサイクルである{{Sfn|Strogatz|2015|pp=216–217}}。 |
|||
上記の微分方程式系にパラメータ {{Mvar|a}} を与えた |
|||
:<math>\begin{align} |
|||
\dot{r} &= r (a - r^2),\\ |
|||
\dot{\theta} &= 1 |
|||
\end{align}</math> |
|||
では、{{Math|''a'' > 0}} であれば、半径 {{Math|{{sqrt|''a''}}}} の円が上記と同様に安定なリミットサイクルである{{Sfn|桑村|2015|pp=51–52}}。しかし {{Math|''a'' < 0}} のときは、全ての軌道は原点に収束する{{Sfn|Hirsch et al.|2007|p=187}}。{{Math|1=''a'' = 0}} のときも、代数的なオーダーの速さだが全ての軌道は原点に収束する{{Sfn|桑村|2015|pp=105–106}}。{{Math|''a'' > 0}} になったときに、原点は不安定となり、原点周囲に安定なリミットサイクルが発生する。よって、この系では {{Math|1=''a'' = 0}} で[[ホップ分岐]]が起きている{{Sfn|桑村|2015|pp=105–106}}{{Sfn|Hirsch et al.|2007|p=187}}。 |
|||
[[File:Van der pols equation phase portrait.svg|thumb|300px|[[ファン・デル・ポール方程式]]における、それぞれのリミットサイクルに漸近する軌道の様子。]] |
|||
上記は解析解を得ることができる例だが、ほとんどの非線形微分方程式系は解析的に解くことはできない{{Sfn|Hirsch et al.|2007|p=144}}。非線形振動現象の代表的な例であり、なおかつ実際の現象に由来する二階非線形微分方程式として、[[バルタザール・ファン・デル・ポール]]が[[三極真空管]]の[[発振回路]]で起こる[[自励振動]]を解明するために導いた[[ファン・デル・ポール方程式]]がある{{Sfn|上田|2008|p=22}}。2次元微分方程式系の形では、ファン・デル・ポール方程式は |
|||
:<math>\begin{align} |
|||
\dot{x} &= x,\\ |
|||
\dot{y} &= \mu (1-x^2)y - x |
|||
\end{align}</math> |
|||
として表される{{Sfn|上田|2008|p=42}}。ここで {{Math|''μ'' > 0}} がパラメータである。 |
|||
上記の例と異なり、このファン・デル・ポール方程式の解は[[初等関数]]で表すことができない{{Sfn|上田|2008|p=42}}。しかし上記の例と同様に、原点周りにリミットサイクルが存在し、初期値が原点を取る場合を除いて全ての軌道がリミットサイクルに収束する。この証明は[[ポアンカレ写像]]を構成する手法で行うことができる{{Sfn|アリグッドほか|2012|pp=132–137}}{{Sfn|Hirsch et al.|2007|pp=268–276}}。あるいは、ファン・デル・ポール方程式は[[リエナール方程式]]の一種であることから、[[リエナールの定理]]よりファン・デル・ポール方程式系の相平面上には唯一の安定なリミットサイクルが存在することがわかる{{Sfn|Strogatz|2015|p=231}}。 |
|||
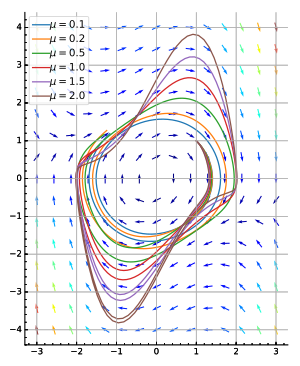
ファン・デル・ポール方程式のリミットサイクルは {{Mvar|μ}} の値によってその形状が変化する。{{Mvar|μ}} が小さいほど、リミットサイクルは円軌道に近づく。{{Mvar|μ}} が大きいほど形状は円から離れていき、{{Mvar|μ}} が大きいほど[[象限|第1象限]]と第3象限で背が高くなる。このとき、[[時系列]]では[[弛張振動]]の様相を示し、緩やかな変化と急な変化の組み合わせから成る振動現象が起きている{{Sfn|上田|2008|pp=42–43}}。 |
|||
===3次元系=== |
|||
{{multiple image |
|||
| align = right |
|||
| direction = vertical |
|||
| footer = [[レスラー方程式]]のリミットサイクル。{{Math|1=''a'' = ''b'' = 0.1}} で固定して、{{Mvar|c}} を変えたとき。 |
|||
| width = 260 |
|||
| image1 = Period-1 limit cycle on Rossler system.png |
|||
| caption1 = 1周期 {{Math|1=(''a'' = 0.1, ''b'' = 0.1, ''c'' = 4)}} |
|||
| image2 = Period-2 limit cycle on Rossler system.png |
|||
| caption2 = 2周期 {{Math|1=(''a'' = 0.1, ''b'' = 0.1, ''c'' = 6)}} |
|||
| image3 = Period-4 limit cycle on Rossler system.png |
|||
| caption3 = 4周期 {{Math|1=(''a'' = 0.1, ''b'' = 0.1, ''c'' = 8.5)}} |
|||
}} |
|||
3次元系においてリミットサイクルが現れる微分方程式系としては、[[レスラー方程式]]や[[ローレンツ方程式]]などがある。[[オットー・レスラー]]が提案したレスラー方程式は |
|||
:<math>\begin{align} |
|||
\dot{x} &= -y-z,\\ |
|||
\dot{y} &= x+ay,\\ |
|||
\dot{z} &= b+xz-cz |
|||
\end{align}</math> |
|||
で表される微分方程式系で、{{Math|''a'', ''b'', ''c''}} がパラメータである。非線形項は第3式の {{Mvar|xz}} のみであるにも関わらず、レスラー方程式の解は様々な振る舞いを見せる<ref>{{cite book ja-jp |title=カオス時系列解析の基礎と応用 |editor=合原一幸 |author=池口徹・山田泰司・小室元政 |publisher=産業図書 |year=2000 |edition=初版 |isbn= 978-4-7828-1010-1}} p. 46.</ref>。 |
|||
例えば、{{Math|1=''a'' = 0.1, ''b'' = 0.1, ''c'' = 4}} というパラメータ値の組み合わせで、レスラー方程式の相空間には安定なリミットサイクルが現れる。ここから、{{Mvar|a}} と {{Mvar|b}} の値は {{Math|0.1}} のままとして {{Mvar|c}} の値を増やしていくと、ある {{Mvar|c}} の値で1重巻きの閉曲線であったリミットサイクルは2重巻きの閉曲線に移り変わる。すなわち、2周して元の状態に戻るような閉曲線になる。パラメータ {{Mvar|c}} の変化によって周期 {{Mvar|T}} の長さがおおよそ倍になる分岐が起きており、このような分岐を[[周期倍分岐]]と呼ぶ{{Sfn|アリグッドほか|2012|pp=192–193}}。リミットサイクルが2重巻きになるには、閉軌道が交差せずに2周できる空間の余地が必要となる。よって、このようなリミットサイクルの周期倍分岐は3次元以上の系でのみ起こる現象である{{Sfn|Strogatz|2015|p=412}}。 |
|||
周期倍分岐を経て、例えば {{Math|1=''a'' = 0.1, ''b'' = 0.1, ''c'' = 6}} のとき、レスラー方程式のリミットサイクルは2重巻き(2周期)の状態にある。さらに {{Mvar|c}} の値を増やしていくと2重巻きのリミットサイクルは4重巻きのリミットサイクルになり、周期はさらに倍になる。以下同様に、{{Mvar|c}} の値の増加に伴って周期倍分岐が起き続け、ある {{Mvar|c}} の値で周期は無限となり、リミットサイクルからカオスへ変わる{{Sfn|アリグッドほか|2012|pp=192–193}}。これは系のアトラクタがカオス(ストレンジアトラクタ)へと分岐するルートの一つで、周期倍分岐ルートと呼ばれる{{Sfn|合原(編)|1990|p=98}}。この例では、 {{Math|1=''a'' = 0.1, ''b'' = 0.1, ''c'' = 9}} のアトラクタはカオスである{{Sfn|アリグッドほか|2012|pp=192–193}}。 |
|||
レスラー方程式は、[[エドワード・ローレンツ]]が提案したローレンツ方程式に触発され、導入されたものであった{{Sfn|合原(編)|1990|p=72}}。ローレンツ方程式でもまた同様に、リミットサイクルの存在と周期倍分岐ルートが確認される{{Sfn|船越|2008|pp=151–155}}。また、[[チュア回路]]では、2つのリミットサイクルが同時に存在する様とそれぞれの周期倍分岐が見られる{{Sfn|アリグッドほか|2012|pp=195–197}}。 |
|||
==実存の現象== |
|||
実存する現象に対して、リミットサイクルは[[自励振動|自励振動現象]]の数理モデルとなり得る{{Sfn|Strogatz|2015|p=215}}。自励振動とは、流入する[[エネルギー]]は非振動的であるにも関わらず、系自身の特性から自ずと発生する振動現象である<ref>{{Cite book ja-jp |editor=日本機械学会 |title=機械工学辞典 |publisher=丸善 |year=2007 |edition=第2版 |isbn=978-4-88898-083-8}} p. 607</ref>。リミットサイクル振動子には、外力による[[強制振動]]の周期に依存せずに系自身でリズムを生み出す自律性がある。また、リミットサイクル振動子に外乱が加わった場合、一時的に振幅が変化するかもしれないが、外乱が無くなれば元の振幅に戻ることができる。このようなリミットサイクルの安定性は、工学的にも生物的にも重要である<ref>{{Cite journal ja-jp |author = 秦 浩起 |year = 2012 |title = リミットサイクル,カオスと同期現象入門 |url =http://www.jspf.or.jp/Journal/PDF_JSPF/jspf2012_07/jspf2012_07-jp.pdf |journal = プラズマ・核融合学会誌 |volume = 88 |issue =7 |publisher = プラズマ・核融合学会 |page = 359}}</ref>。 |
|||
[[File:Wittner metronome.jpg|thumb|190px|初期状態に依存せずに安定なリズムを作る[[メトロノーム]]]] |
|||
一定のリズムを鳴らす機械式の[[メトロノーム]]は安定なリズムの好例である。最初に針を小さく振って動かしたとしても、針を大きく振って動かしたとしても、メトロノームは一定の振動に落ち着く。メトロノームの減衰力と駆動力がバランスすることによって安定な振動を生み出しており、簡単なモデル化によってもメトロノームにおけるリミットサイクルの存在が確認できる{{Sfn|郡・森田|2011|pp=10–11, 18–20}}。また例えば心臓の[[拍動]]などのように、生物のリズム現象の多くは(生物分野では[[恒常性]]と呼ばれる)安定性を持っている。このような安定なリズムを記述するのにリミットサイクルを持つモデルが有効である{{Sfn|郡・森田|2011|pp=9–10, 17}}。 |
|||
== 関連項目 == |
== 関連項目 == |
||
*[[非線形振動子]] |
*[[非線形振動子]] |
||
*[[安定多様体]] |
*[[安定多様体]] |
||
*[[アトラクター]] |
|||
*[[蔵本モデル]] |
*[[蔵本モデル]] |
||
*[[ファレイ数列#非線形現象に現れるファレイ数列|非線形現象に現れるファレイ数列]] |
*[[ファレイ数列#非線形現象に現れるファレイ数列|非線形現象に現れるファレイ数列]] |
||
==脚注== |
|||
{{Reflist|2}} |
|||
==参照文献== |
|||
*{{Cite book ja-jp |
|||
|author=Steven H. Strogatz |
|||
|translator=田中 久陽・中尾 裕也・千葉 逸人 |
|||
|title=ストロガッツ 非線形ダイナミクスとカオス―数学的基礎から物理・生物・化学・工学への応用まで |
|||
|publisher=丸善出版 |
|||
|year=2015 |
|||
|isbn=978-4-621-08580-6 |
|||
|ref={{Sfnref|Strogatz|2015}} |
|||
}} |
|||
*{{Cite book ja-jp |
|||
|author=郡 宏・森田 善久 |
|||
|title=生物リズムと力学系 |
|||
|series=シリーズ・現象を解明する数学 |
|||
|publisher=共立出版 |
|||
|year=2011 |
|||
|edition=初版 |
|||
|isbn=978-4-320-11000-7 |
|||
|ref={{Sfnref|郡・森田|2011}} |
|||
}} |
|||
*{{Cite book ja-jp |
|||
|author=桑村 雅隆 |
|||
|title=パターン形成と分岐理論―自発的パターン発生の力学系入門 |
|||
|series=シリーズ・現象を解明する数学 |
|||
|publisher=共立出版 |
|||
|year=2015 |
|||
|edition=初版 |
|||
|isbn=978-4-320-11004-5 |
|||
|ref={{Sfnref|桑村|2015}} |
|||
}} |
|||
*{{Cite book ja-jp |
|||
|author=船越 満明 |
|||
|title=カオス |
|||
|series=シリーズ 非線形科学入門3 |
|||
|publisher=朝倉書店 |
|||
|year=2008 |
|||
|edition=初版 |
|||
|isbn=978-4-254-11613-7 |
|||
|ref={{Sfnref|船越|2008}} |
|||
}} |
|||
*{{Cite book ja-jp |
|||
|author=Morris W. Hirsch; Stephen Smale; Robert L. Devaney |
|||
|translator=桐木 紳・三波 篤朗・谷川 清隆・辻井 正人 |
|||
|title=力学系入門 原著第2版―微分方程式からカオスまで |
|||
|publisher=共立出版 |
|||
|edition=初版 |
|||
|year=2007 |
|||
|isbn=978-4-320-01847-1 |
|||
|ref={{Sfnref|Hirsch et al.|2007}} |
|||
}} |
|||
*{{Cite book ja-jp |
|||
|author=上田睆亮 |
|||
|title=カオス現象論 |
|||
|series=現代非線形科学シリーズ12 |
|||
|publisher=コロナ社 |
|||
|year=2008 |
|||
|edition=初版 |
|||
|isbn=978-4-339-02611-5 |
|||
|ref={{Sfnref|上田|2008}} |
|||
}} |
|||
*{{Cite book ja-jp |
|||
|author=K.T.アリグッド・T.D.サウアー・J.A.ヨーク |
|||
|translator =星野高志・阿部巨仁・黒田拓・松本和宏 |
|||
|others=津田一郎(監訳) |
|||
|editor=シュプリンガー・ジャパン |
|||
|title=カオス 第2巻 力学系入門 |
|||
|publisher=丸善出版 |
|||
|year=2012 |
|||
|isbn=978-4-621-06279-1 |
|||
|ref={{Sfnref|アリグッドほか|2012}} |
|||
}} |
|||
*{{Cite book ja-jp |
|||
|author=S. ウィギンス |
|||
|translator =今井 桂子・田中 茂・水谷 正大・森 真 |
|||
|others=丹羽 敏雄(監訳) |
|||
|title=非線形の力学系とカオス |
|||
|edition=新装版 |
|||
|publisher=丸善出版 |
|||
|editor=シュプリンガー・ジャパン |
|||
|year=2013 |
|||
|isbn=978-4-621-06435-1 |
|||
|ref={{Sfnref|ウィギンス|2013}} |
|||
}} |
|||
*{{Cite book ja-jp |
|||
|title=カオス ―カオス理論の基礎と応用 |
|||
|editor=合原一幸 |
|||
|author=香田徹・小室元政・松本隆・CHUA, Leon O.・徳永隆治・相沢洋二・大石真一・八幡 |
|||
|publisher=サイエンス社 |
|||
|year=1990 |
|||
|edition=初版 |
|||
|isbn= 4-7819-0592-7 |
|||
|ref={{Sfnref|合原(編)|1990}} |
|||
}} |
|||
*{{Cite web |
|||
|author=川上 博 |
|||
|year=2005 |
|||
|url=http://cms.db.tokushima-u.ac.jp/DAV/lecture/125260/LectureNote/2006/NonlinearPhenomena.pdf |
|||
|title=非線形現象入門 |
|||
|accessdate=2018-06-14 |
|||
|website= 徳島大学 教育・研究者情報データベース |
|||
|ref={{Sfnref|川上|2005}} |
|||
}} |
|||
*{{Cite web |
|||
|date=2010-09-16 |
|||
|url=http://www.ieice-hbkb.org/files/01/01gun_11hen_01.pdf |
|||
|title=1群11編 非線形問題 1章 非線形力学系 |
|||
|accessdate=2018-06-16 |
|||
|work=電子情報通信学会知識ベース |
|||
|pages=1–13 |
|||
|ref={{Sfnref|電子情報通信学会知識ベース|2010}} |
|||
}} |
|||
==外部リンク== |
|||
*{{Commonscat-inline}} |
|||
*{{YouTube|0KV0Odhcl9g|Chaos4 Japanese(カオス4 ブランコ)}} 力学系、バタフライ効果、カオス理論に関する一般向けビデオ「CHAOS」、第4章、日本語訳:坪井俊 |
|||
{{DEFAULTSORT:りみつとさいくる}} |
{{DEFAULTSORT:りみつとさいくる}} |
||
[[Category:力学系]] |
[[Category:力学系]] |
||
[[Category:極限集合]] |
[[Category:極限集合]] |
||
[[Category:閉曲線]] |
|||
[[Category:数学に関する記事]] |
[[Category:数学に関する記事]] |
||
2018年6月17日 (日) 14:01時点における版

リミットサイクル(英語:limit cycle)とは、力学系における相空間上での閉軌道であり、時間 t を無限大、またはマイナス無限大にしたとき、その閉軌道に収束する軌道が少なくとも一つ存在するものである。極限閉軌道や極限周期軌道とも呼ばれる。1881年、力学系の始祖でもあるアンリ・ポアンカレによって初めて見いだされた[1]。
リミットサイクルは非線形系でのみ現れる。リミットサイクルの十分近くの軌道がすべてリミットサイクルに収束するとき、漸近安定である、または単に安定であるという。
安定なリミットサイクルは、閉軌道に小さな摂動が加わっても元に戻る。物理的には、リミットサイクルは自励振動の数理モデルとなる。また、相空間上の様々な初期値から出発した軌道はリミットサイクル軌道に収束し、やはり自励振動を示す。リミットサイクルを持つ例として、ファン・デル・ポール振動子がある。代数的微分方程式におけるリミットサイクル軌道の数を求める問題は、ヒルベルトの第16問題の第二の問題として知られる。2次元相空間の場合は、ポアンカレ・ベンディクソンの定理などによってリミットサイクルの存在(または非存在)を予見できる。
定義
系の時間を t ∈ R、状態変数を X = (x1, x2,... xn) ∈ Rn とする。n 次元連続力学系のある解 X(t) が平衡点ではなく、なおかつ X(t) = X(t + T) を満たすような T > 0 が存在するとき、X(t) は閉軌道(あるいは周期軌道、周期解)と呼ばれる[2]。特に X(t) = X(t + T) を満たす最小の T を周期と呼ぶ。閉軌道となる解 X(t) を C で表すとする。系の相空間 x1, x2,... xn 上で、閉軌道 C は単純閉曲線を描く[3]。
リミットサイクルは次のように定義される。ある閉軌道 C が存在するとする。C のある近傍で任意の初期点(初期値)X0 を取り、X0 を通る解 ϕ (t, X0) が t → ∞ または t → −∞ で ϕ (t, X0) が C に漸近するとき、C はリミットサイクルと呼ばれる[4]。あるいは、
または
となる C と X0 ∉ C が存在するとき、C はリミットサイクルと呼ばれる。ここで、d(ϕ(t, X0), C) は時刻 t における点 ϕ (t, X0) と集合 C の距離である[5]。
リミットサイクル型の振動を示す系をリミットサイクル振動子などとも呼ぶ[6]。「リミット」は極限集合を意味し[6]、リミットサイクルは極限閉軌道[7]や極限周期軌道[8]とも呼ばれる。極限集合には t → ∞ 方向の ω 極限集合と t → −∞ 方向の α 極限集合の2つがある。極限集合を用いてリミットサイクルを定義すれば、閉軌道 C が存在し、X0 ∉ C の ω 極限集合 ω(X0) または α 極限集合 α(X0) が C となるとき、ω(X0) または α(X0) はリミットサイクルと呼ばれる[9]。
2次元連続力学系では、相平面上でリミットサイクルは必ず孤立した閉軌道となる。すなわち、リミットサイクルとなる閉軌道 C の近傍には他の閉軌道は存在し得ない。C 近傍の全ての軌道は、C に吸引されるように近づくか、C から反発するように遠ざかるかの2通りしかない[10]。周りの軌道を吸引するリミットサイクルは漸近安定あるいは単に安定であるという。安定なリミットサイクルはアトラクタの一種である[11]。安定なリミットサイクルのことを周期アトラクタともいう[12]。
周りの軌道を反発するリミットサイクルは軌道不安定あるいは単に不安定であるという[11]。相平面のリミットサイクルで、内側の軌道が吸引されて外側の軌道が反発するような場合、あるいは内側の軌道が反発して外側の軌道が吸引されるような場合、これらの場合のリミットサイクルは半安定であるという[13][10]。
存在条件
実直線上の1次元自律系の微分方程式系では、周期解は存在し得ない[14]。2次元自律系あるいは1次元非自律系以上から周期解が現れるようになる[15]。また、リミットサイクルは非線形の系のみで起こる現象である。線形の系ではリミットサイクルは起こらない[16][17]。
流れに沿って相空間の体積が変化しない系を保存系と呼び、体積が零に漸近する系を散逸系と呼ぶ[18]。散逸系の場合にリミットサイクルが存在する[19]。周期軌道が散逸系で存在する場合、それらの周期軌道の大抵はリミットサイクルであると推定される[20]。系が勾配系である場合も、リミットサイクルは存在しない[21]。
以下、変数の時間微分 d/dt を変数の上部に · を付けて表す(ニュートンの記法)。もし、系を2次元自律系
に限定すれば、閉軌道およびリミットサイクルの有無が判別できる定理がいくつかある。ポアンカレ・ベンディクソンの定理により、平衡点を含まない有界な軌道の極限集合は閉軌道である[22]。すなわち、このような軌道は閉軌道そのものか、存在するリミットサイクルに吸引される軌道であるかのどちらかである[23]。さらに、ベンディクソンの否定条件によれば、単連結な領域 Ω 上で
の値が零ではなく、かつ符号が一定であれば、Ω に完全に含まれる閉軌道は存在しない[24]。また、系がリエナール方程式に相当するのであれば、リエナールの定理より原点を囲む漸近安定なリミットサイクルの存在する[25]。
力学系のパラメータ(定数係数)が変化することによって、解に定性的な変化が起こることを分岐という[26]。リミットサイクルも分岐を経て発生する。2次元系でリミットサイクルが発生する典型的な分岐は、ホップ分岐と呼ばれる分岐である[27]。ホップ分岐では、パラメータ変化によって安定な平衡点が不安定に遷移し、その周囲に安定なリミットサイクルが起こる。あるいは、安定な平衡点と不安定なリミットサイクルが不安定な平衡点に遷移する場合もある[28]。ホップ分岐は局所分岐の一種である。リミットサイクルが関わる大域分岐としては、ホモクリニック分岐やリミットサイクル同士が衝突するサドルノード分岐などがある[29]。

周期軌道の安定性は、ポアンカレ写像の構成や周期軌道周りの変分方程式(線形化方程式)の構成から判別できる。適当な n − 1 次元の局所断面を取り、ポアンカレ写像を設定することで連続力学系の周期解を離散力学系の写像に置き換えることができる。写像が漸近安定な不動点を持つ場合は元の周期軌道が漸近安定である[30]。ポアンカレ写像は、リミットサイクルを見出したポアンカレ自身がリミットサイクルを考察するために生み出した手法である[31]。あるいは、周期軌道からの微小なズレを想定して周期軌道に対する変分方程式を構成することによって、フロケ理論を適用することができる。変分方程式のフロケ乗数あるいはフロケ指数から周期軌道の安定性が決定できる[32][33]。ただし、ポアンカレ写像による方法も線形化方程式による方法も、任意の微分方程式系に適用できる解析的な一般的手法は存在しない。ポアンカレ写像であれば対称の系ごとに個別に工夫して構成する必要があり、フロケ乗数による判定であれば数値計算による手法がある[34][35]。
具体例
2次元系

リミットサイクルが現れる簡単な微分方程式系の例として、
という2次元系がある[36][37]。この系を極座標で表せば、
となり、動径 r と偏角 θ の振る舞いが互いに無関係に決まる単純な形となる[38]。θ(t) の一般解は一定振動数で回転し続ける関数となる。r(t) の一般解は
という関数となる。ここで、r0 は t = 0 における r の値である。よって、r0 ≠ 0 であれば、r(t) は t → ∞ で r → 1 であり、系の原点を除く全ての軌道は回転しながら単位円に近づいていくこととなる[37]。この結果は、明示的な一般解を必要としない簡易な安定判別によっても得られる。よって、原点を中心とする単位円がこの系の安定なリミットサイクルである[39]。
上記の微分方程式系にパラメータ a を与えた
では、a > 0 であれば、半径 √a の円が上記と同様に安定なリミットサイクルである[40]。しかし a < 0 のときは、全ての軌道は原点に収束する[41]。a = 0 のときも、代数的なオーダーの速さだが全ての軌道は原点に収束する[42]。a > 0 になったときに、原点は不安定となり、原点周囲に安定なリミットサイクルが発生する。よって、この系では a = 0 でホップ分岐が起きている[42][41]。
上記は解析解を得ることができる例だが、ほとんどの非線形微分方程式系は解析的に解くことはできない[43]。非線形振動現象の代表的な例であり、なおかつ実際の現象に由来する二階非線形微分方程式として、バルタザール・ファン・デル・ポールが三極真空管の発振回路で起こる自励振動を解明するために導いたファン・デル・ポール方程式がある[44]。2次元微分方程式系の形では、ファン・デル・ポール方程式は
として表される[45]。ここで μ > 0 がパラメータである。
上記の例と異なり、このファン・デル・ポール方程式の解は初等関数で表すことができない[45]。しかし上記の例と同様に、原点周りにリミットサイクルが存在し、初期値が原点を取る場合を除いて全ての軌道がリミットサイクルに収束する。この証明はポアンカレ写像を構成する手法で行うことができる[46][47]。あるいは、ファン・デル・ポール方程式はリエナール方程式の一種であることから、リエナールの定理よりファン・デル・ポール方程式系の相平面上には唯一の安定なリミットサイクルが存在することがわかる[48]。
ファン・デル・ポール方程式のリミットサイクルは μ の値によってその形状が変化する。μ が小さいほど、リミットサイクルは円軌道に近づく。μ が大きいほど形状は円から離れていき、μ が大きいほど第1象限と第3象限で背が高くなる。このとき、時系列では弛張振動の様相を示し、緩やかな変化と急な変化の組み合わせから成る振動現象が起きている[49]。
3次元系
3次元系においてリミットサイクルが現れる微分方程式系としては、レスラー方程式やローレンツ方程式などがある。オットー・レスラーが提案したレスラー方程式は
で表される微分方程式系で、a, b, c がパラメータである。非線形項は第3式の xz のみであるにも関わらず、レスラー方程式の解は様々な振る舞いを見せる[50]。
例えば、a = 0.1, b = 0.1, c = 4 というパラメータ値の組み合わせで、レスラー方程式の相空間には安定なリミットサイクルが現れる。ここから、a と b の値は 0.1 のままとして c の値を増やしていくと、ある c の値で1重巻きの閉曲線であったリミットサイクルは2重巻きの閉曲線に移り変わる。すなわち、2周して元の状態に戻るような閉曲線になる。パラメータ c の変化によって周期 T の長さがおおよそ倍になる分岐が起きており、このような分岐を周期倍分岐と呼ぶ[51]。リミットサイクルが2重巻きになるには、閉軌道が交差せずに2周できる空間の余地が必要となる。よって、このようなリミットサイクルの周期倍分岐は3次元以上の系でのみ起こる現象である[52]。
周期倍分岐を経て、例えば a = 0.1, b = 0.1, c = 6 のとき、レスラー方程式のリミットサイクルは2重巻き(2周期)の状態にある。さらに c の値を増やしていくと2重巻きのリミットサイクルは4重巻きのリミットサイクルになり、周期はさらに倍になる。以下同様に、c の値の増加に伴って周期倍分岐が起き続け、ある c の値で周期は無限となり、リミットサイクルからカオスへ変わる[51]。これは系のアトラクタがカオス(ストレンジアトラクタ)へと分岐するルートの一つで、周期倍分岐ルートと呼ばれる[53]。この例では、 a = 0.1, b = 0.1, c = 9 のアトラクタはカオスである[51]。
レスラー方程式は、エドワード・ローレンツが提案したローレンツ方程式に触発され、導入されたものであった[54]。ローレンツ方程式でもまた同様に、リミットサイクルの存在と周期倍分岐ルートが確認される[55]。また、チュア回路では、2つのリミットサイクルが同時に存在する様とそれぞれの周期倍分岐が見られる[56]。
実存の現象
実存する現象に対して、リミットサイクルは自励振動現象の数理モデルとなり得る[16]。自励振動とは、流入するエネルギーは非振動的であるにも関わらず、系自身の特性から自ずと発生する振動現象である[57]。リミットサイクル振動子には、外力による強制振動の周期に依存せずに系自身でリズムを生み出す自律性がある。また、リミットサイクル振動子に外乱が加わった場合、一時的に振幅が変化するかもしれないが、外乱が無くなれば元の振幅に戻ることができる。このようなリミットサイクルの安定性は、工学的にも生物的にも重要である[58]。

一定のリズムを鳴らす機械式のメトロノームは安定なリズムの好例である。最初に針を小さく振って動かしたとしても、針を大きく振って動かしたとしても、メトロノームは一定の振動に落ち着く。メトロノームの減衰力と駆動力がバランスすることによって安定な振動を生み出しており、簡単なモデル化によってもメトロノームにおけるリミットサイクルの存在が確認できる[59]。また例えば心臓の拍動などのように、生物のリズム現象の多くは(生物分野では恒常性と呼ばれる)安定性を持っている。このような安定なリズムを記述するのにリミットサイクルを持つモデルが有効である[60]。
関連項目
脚注
- ^ P. Yu & W. Lin (2016) Complex dynamics in biological systems arising from multiple limit cycle bifurcation, Journal of Biological Dynamics, 10:1, 263-285, doi:10.1080/17513758.2016.1166270
- ^ Strogatz 2015, p. 161.
- ^ アリグッドほか 2012, p. 149.
- ^ Strogatz 2015, p. 214 訳注より.
- ^ Hirsch et al. 2007, pp. 229–232.
- ^ a b 郡・森田 2011, p. 17.
- ^ ラルフ・エイブラハム、ヨシスケ・ウエダ(編)、稲垣耕作・赤松則男(訳)、2002、『カオスはこうして発見された』初版、共立出版 ISBN 4-320-03418-X p. 31.
- ^ 船越 2008, p. 84.
- ^ 郡・森田 2011, p. 53.
- ^ a b Strogatz 2015, p. 214.
- ^ a b 郡・森田 2011, pp. 17, 121.
- ^ 井庭崇・福原義久、1998年、『複雑系入門―知のフロンティアへの冒険』初版、NTT出版 ISBN 4-87188-560-7 p. 69.
- ^ 下郷太郎・田島清灝、2002、『振動学』初版、コロナ社〈機械系 大学講義シリーズ11〉 ISBN 4-339-04045-2 p. 148.
- ^ Strogatz 2015, pp. 32–33.
- ^ Hirsch et al. 2007, pp. 10–11.
- ^ a b Strogatz 2015, p. 215.
- ^ 郡・森田 2011, pp. 17–18.
- ^ 電子情報通信学会知識ベース 2010, p. 3.
- ^ 郡・森田 2011, p. 16.
- ^ 川上 2005, p. 65.
- ^ 桑村 2015, p. 63.
- ^ Hirsch et al. 2007, p. 229.
- ^ 川上 2005, p. 160.
- ^ ウィギンス 2013, p. 27.
- ^ Strogatz 2015, p. 230.
- ^ 電子情報通信学会知識ベース 2010, p. 12.
- ^ Strogatz 2015, pp. 285.
- ^ ウィギンス 2013, pp. 276–277.
- ^ Strogatz 2015, pp. 285–289.
- ^ ウィギンス 2013, pp. 64–69.
- ^ 電子情報通信学会知識ベース 2010, p. 4.
- ^ 桑村 2015, pp. 53–56.
- ^ 郡・森田 2011, pp. 116–122.
- ^ ウィギンス 2013, p. 65.
- ^ 桑村 2015, p. 58.
- ^ Strogatz 2015, p. 261.
- ^ a b M. ブラウン、シュプリンガー・ジャパン(編)、一樂重雄・河原正治・河原雅子・一樂祥子(訳)、2012、『微分方程式 下―その数学と応用』、丸善出版 ISBN 978-4-621-06234-0 pp. 211–212.
- ^ Strogatz 2015, p. 216.
- ^ Strogatz 2015, pp. 216–217.
- ^ 桑村 2015, pp. 51–52.
- ^ a b Hirsch et al. 2007, p. 187.
- ^ a b 桑村 2015, pp. 105–106.
- ^ Hirsch et al. 2007, p. 144.
- ^ 上田 2008, p. 22.
- ^ a b 上田 2008, p. 42.
- ^ アリグッドほか 2012, pp. 132–137.
- ^ Hirsch et al. 2007, pp. 268–276.
- ^ Strogatz 2015, p. 231.
- ^ 上田 2008, pp. 42–43.
- ^ 池口徹・山田泰司・小室元政、合原一幸(編)、2000、『カオス時系列解析の基礎と応用』初版、産業図書 ISBN 978-4-7828-1010-1 p. 46.
- ^ a b c アリグッドほか 2012, pp. 192–193.
- ^ Strogatz 2015, p. 412.
- ^ 合原(編) 1990, p. 98.
- ^ 合原(編) 1990, p. 72.
- ^ 船越 2008, pp. 151–155.
- ^ アリグッドほか 2012, pp. 195–197.
- ^ 日本機械学会(編)、2007、『機械工学辞典』第2版、丸善 ISBN 978-4-88898-083-8 p. 607
- ^ 秦 浩起、2012、「リミットサイクル,カオスと同期現象入門」、『プラズマ・核融合学会誌』88巻7号、プラズマ・核融合学会 p. 359
- ^ 郡・森田 2011, pp. 10–11, 18–20.
- ^ 郡・森田 2011, pp. 9–10, 17.
参照文献
- Steven H. Strogatz、田中 久陽・中尾 裕也・千葉 逸人(訳)、2015、『ストロガッツ 非線形ダイナミクスとカオス―数学的基礎から物理・生物・化学・工学への応用まで』、丸善出版 ISBN 978-4-621-08580-6
- 郡 宏・森田 善久、2011、『生物リズムと力学系』初版、共立出版〈シリーズ・現象を解明する数学〉 ISBN 978-4-320-11000-7
- 桑村 雅隆、2015、『パターン形成と分岐理論―自発的パターン発生の力学系入門』初版、共立出版〈シリーズ・現象を解明する数学〉 ISBN 978-4-320-11004-5
- 船越 満明、2008、『カオス』初版、朝倉書店〈シリーズ 非線形科学入門3〉 ISBN 978-4-254-11613-7
- Morris W. Hirsch; Stephen Smale; Robert L. Devaney、桐木 紳・三波 篤朗・谷川 清隆・辻井 正人(訳)、2007、『力学系入門 原著第2版―微分方程式からカオスまで』初版、共立出版 ISBN 978-4-320-01847-1
- 上田睆亮、2008、『カオス現象論』初版、コロナ社〈現代非線形科学シリーズ12〉 ISBN 978-4-339-02611-5
- K.T.アリグッド・T.D.サウアー・J.A.ヨーク、シュプリンガー・ジャパン(編)、津田一郎(監訳)、星野高志・阿部巨仁・黒田拓・松本和宏(訳)、2012、『カオス 第2巻 力学系入門』、丸善出版 ISBN 978-4-621-06279-1
- S. ウィギンス、シュプリンガー・ジャパン(編)、丹羽 敏雄(監訳)、今井 桂子・田中 茂・水谷 正大・森 真(訳)、2013、『非線形の力学系とカオス』新装版、丸善出版 ISBN 978-4-621-06435-1
- 香田徹・小室元政・松本隆・CHUA, Leon O.・徳永隆治・相沢洋二・大石真一・八幡、合原一幸(編)、1990、『カオス ―カオス理論の基礎と応用』初版、サイエンス社 ISBN 4-7819-0592-7
- 川上 博 (2005年). “非線形現象入門”. 徳島大学 教育・研究者情報データベース. 2018年6月14日閲覧。
- “1群11編 非線形問題 1章 非線形力学系”. 電子情報通信学会知識ベース. pp. 1–13 (2010年9月16日). 2018年6月16日閲覧。
外部リンク
 ウィキメディア・コモンズには、リミットサイクルに関するカテゴリがあります。
ウィキメディア・コモンズには、リミットサイクルに関するカテゴリがあります。- Chaos4 Japanese(カオス4 ブランコ) - YouTube 力学系、バタフライ効果、カオス理論に関する一般向けビデオ「CHAOS」、第4章、日本語訳:坪井俊















