モルワイデ図法

モルワイデ図法で表した地球

モルワイデ図法の経緯線

地球温暖化の観測例として、1995-2005年の平均気温の1940-1980年の平均に対する差を示したもの。一部地域を拡大して偏った印象を与えないように、正積図法のモルワイデ図法で描かれている。

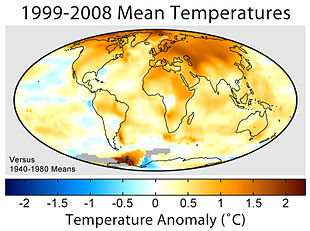
モルワイデ図法（モルワイデずほう）は、1805年にドイツの天文学者・数学者カール・モルワイデが考案した地図投影法の一種である。

特徴

擬円筒図法の一種で、地図上の任意の場所で実際の面積との比が等しくなる正積図法である。地球全体を1枚の平面に表現でき、地図の外周は楕円形になる。楕円の長径（横）と短径（縦）の比は2:1となり、もし縮尺1分の1の地図を作成したとすれば、横36040km、縦18020kmの楕円となる。

緯線はどれも水平な直線になる。経線は中央経線が垂直な直線となるが、それ以外の経線は弧を描く。等積になるように緯線の間隔を調整するため、距離の比は一定になっていない。赤道上では正角でなく、南北方向が東西方向に比べ1.234倍伸びている。中央経線上で正角になるのは緯度40度44分である。地図の周辺部の歪みが大きくなるが、サンソン図法ほど大きくはない。

主に分布図に利用される。

表式

地球を半径1の球とし、赤道上を縮尺1でモルワイデ図法に投影する場合、経度 λ、緯度 φ に対応する点は

$X=\lambda\cos\theta$

$Y=\frac{\pi}{2}\sin\theta$

ただし θ はラジアン単位で次の式を満たす数である：

$\pi\sin\phi=\sin 2\theta+2\theta$

赤道縮尺1のモルワイデ図法の面積は地球表面積の π²/8≒1.234倍であり、正積図法ゆえどの点でもこの面積倍率である。中央経線上での縦横の歪みは (π²/8)(cosφ/cosθ)² になる。

緯度$\phi\,$とY座標の関係

緯度$\phi\,$	媒介変数$\theta\,$	$\sin\theta\,$	歪み$\frac{\pi^2}{8}\left(\frac{\cos\phi}{\cos\theta}\right)^2$
0rad=0°	0rad=0°	0	1.23377
π/18rad=10°	0.13724rad= 7.863°	0.13681	1.21932
π/9rad=20°	0.27549rad=15.784°	0.27202	1.17643
π/6rad=30°	0.41586rad=23.827°	0.40398	1.10573
2π/9rad=40°	0.55975rad=32.071°	0.53097	1.00822
5π/18rad=50°	0.70911rad=40.629°	0.65116	0.88497
π/3rad=60°	0.86699rad=49.675°	0.76238	0.73650
7π/18rad=70°	1.03902rad=59.531°	0.86191	0.56129
4π/9rad=80°	1.23880rad=70.978°	0.94539	0.35019
π/2rad=90°	1.57079rad=90°	1	→0

関連項目

• 世界地図
• メルカトル図法
• ボンヌ図法
• ミラー図法
• ランベルト正積方位図法
• ランベルト正角円錐図法

外部リンク

• 地図投影法 / 投影法カタログ / モルワイデ図法