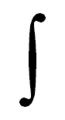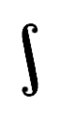積分記号

∫

積分記号（せきぶんきごう、英語: Integral symbol）は、積分を表す演算子である。Sを縦方向に長くした記号が使用される。

正式な名前は定められていないが、本稿では習慣上呼ばれている「積分記号」とする（他の呼び方については「呼び方」を参照のこと。）。

概要

積分記号はドイツの数学者のゴットフリート・ライプニッツによって17世紀末に発表された。長いs（ſ）を変形させた記号である。

この記号はSの形を上下に伸ばした形を書く場合と、斜めに寝かせたものとがある。

定積分の場合は、積分記号の右下に下端を書き、右上に上端を書く（下に下端、上に上端を書くこともある）。あるいは、積分記号の右下に積分領域を書く。

• 使用例（関数$\ f(x)$の不定積分$\ F(x)$、集合$\ D$上での$\ f(x)$の積分$\ I$）

$F(x)=\int f(x)dx,\quad I=\int _{D}f(x)dx$

呼び方

「積分記号」や単にインテグラル（Integral）と呼ばれる。

数式を口頭で伝える場合や数学の授業で本記号を示す場合は「インテグラル」と発音することが多い。単に「積分する」と説明することもある。以下の例では「インテグラル エックス二乗 ディーエックス」や「エックスの二乗をエックスで積分する」などと口述する。；

• $\int x^{2}dx$

著名な本や有名人が呼称に関して言及している例

• リチャード・P・ファインマンはファインマン物理学の中で本記号を「積分の記号」ということを「どうもあまり関心しない」としている。
• 『マセマ出版社』の初学者向け参考書では「インテグラルと読む」と説明している。

類似する記号

資生堂のロゴ。Sの字体が積分記号に類似している。

• 無声後部歯茎摩擦音（ʃ） - 舌を後部歯茎に接近させて調音される無声の摩擦音を示す記号。
• f字孔 - ヴァイオリンなどの弦楽器に開けられたサウンドホールの形状。fの横棒は非常に小さいため積分記号に見える。楽器によっては横棒が省略され積分記号と変わらないものもある。
• 積分記号に類似した字体のS - 資生堂のロゴなど。

二重積分記号

∬

二重積分に用いられる記号で、積分記号を2つ並べた記号である。

• 使用例（集合$\ D$上での関数$\ f(x,y)$の積分$\ V$）

$V=\iint _{D}f(x,y)dxdy$

閉路積分記号

∮

周回積分に用いられる記号で、積分記号の中央に丸を書く。

• 使用例（グリーンの定理）

$\oint _{\partial D}\left(Pdx+Qdy\right)=\iint _{D}\left({\frac {\partial Q}{\partial x}}-{\frac {\partial P}{\partial y}}\right)dxdy$

他言語での活字体

他の言語においては、積分記号の形状は英語の書物においてよく見られるものと若干異なっている。

• 
  英語の数学書においては、積分記号は右傾している
• 
  ドイツにおける記号は直状となっている
• 
  ロシアにおける積分記号は左傾している（ドイツ式記号もしばしばロシアの書物に見られる）
• 
  数研出版の出版物・プリント制作ソフトの積分記号，下端と上端が揃うため見た目が綺麗である。

他の相違点は定積分における上下端の位置である。英語の書物においては、上下端は積分記号の右に位置する: $\int _{0}^{T}f(t)\;dt$

一方、ドイツやロシアの書物においては、上下端は積分記号の上下に位置し、記述にはより多くのスペースを要することとなる: $\int \limits _{0}^{T}f(t)\;\mathrm {d} t$

符号位置

記号	Unicode	JIS X 0213	文字参照	名称
∫	U+222B	1-2-73	∫ ∫ ∫	積分記号
∬	U+222C	1-2-74	∬ ∬	二重積分記号
∮	U+222E	1-13-83	∮ ∮	周回積分記号

関連項目

• 積分
• プライム