九点円

九点円(きゅうてんえん、英: nine-point circle)は、三角形において特定の9個の点を通る円の名称である。発見した人の名前から、オイラー円(英: Euler's circle)・フォイエルバッハ円(英: Feuerbach circle)とも呼ばれる[1]。
概要[編集]
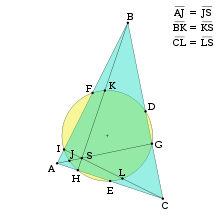
九点円は三角形ABCの以下の9個の点を通る[2]。
- 3辺の中点(D、E、F)
- 3頂点から対辺に下ろした垂線の足(G、H、I)
- 垂心と3頂点の中点(J、K、L)
九点円の中心Nはオイラー線上の垂心と外心の中点であり、半径は外接円の半径Rの半分R/2である[注釈 1]。
歴史[編集]
三角形上の6個の点(上述の点のうち辺上にあるもの)を通る円の存在をオイラーが1765年に証明していたともいわれる[1]。
九点円が三角形上の6個の点に加えて残りの3点を通ることは、フランスのジャン=ヴィクトル・ポンスレとシャルル・ブリアンションによって1821年に証明された。その翌年の1822年に、ドイツのカール・フォイエルバッハが同じ円が三角形の内接円と傍接円に接することも含めてモノグラフで証明を発表した[4]。さらにその後の1842年に、フランスのオルリー・テルケムがフォイエルバッハの定理の解析的な証明を与え、この円を九点円(仏: le cercle des neuf points、英: nine point circle)と命名した。この円は六点円とも呼ばれていたが、現在六点円は三角形上の別の円を指す名称となっている。
証明[編集]
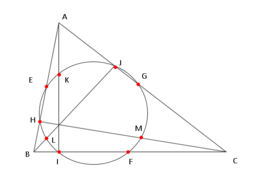
右図で四角形ELMGを作る。中点連結定理より、EG, LM, BCは平行となり、EL, AI, GMも平行となる。AI, BCは垂直となる。以上より、四角形ELMGは長方形で、その4つの頂点は同一円周Γ上にある。したがって、この長方形ELMGの対角線EM, LGは、円Γの直径となる。角LJGは90゜だから、JはLGを直径とする円Γ上にあることが分かる。同様にHもEMを直径とする円Γ上にある。
次に、四角形KLFGについて同様に議論すると、四角形KLFGは長方形となる。したがって、その4つの頂点は同一円周Γ'上にあり、IはKFを直径とする円Γ'上に, JもLGを直径とする円Γ'上にあることが分かる。
しかし、LGを直径とする円は一つしかないので、上記の二つの円Γ, Γ'は一致する。
以上より、9点が同一円周Γ上にあることが分かる[2][5]。
関連する性質[編集]
フォイエルバッハの定理[編集]
フォイエルバッハは、1822年に以下の定理を証明している[4][6]。
この定理は「フォイエルバッハの定理」と呼ばれる、九点円に関する最も有名な定理のひとつである。
九点円と内接円の接点をフォイエルバッハ点と呼ぶ[7]。この定理は第三フォンテーネの定理として一般化されている。
その他の性質[編集]
他に以下のような性質がある。
- 三角形の3個の頂点と垂心の4点からどの3個を選んでも、その三角形に対する九点円は同じになる[8]。
- 外接円の対蹠点上にある2点から導かれる2本のシムソン線は、九点円上で直交する[注釈 2]。
- 垂心と外接円上の任意の点の中点は九点円上にある[注釈 3]。
また、九点円の定理から以下のことも導かれる。
-
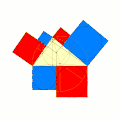
図のように三角形(黄)の九点円(緑)の中心から当該三角形の各辺への垂線として交わる点で辺を分割して分割後の長さの辺を持つ正方形6個を描き、それらの正方形の面積の巡回奇偶別合計を求めると、両合計面積(赤・青)は等しくなっている。
-
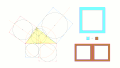
図のように三角形(黄)の底辺が当該三角形の九点円(緑)の中心からの垂線で分割されている場合、分割後の長さの辺(紫・桃)を持つ正方形同士の面積の差は、頂点へ向けての二辺それぞれを辺として持つ正方形(赤・青)同士の面積の差の半分となっている。
脚注[編集]
注釈[編集]
- ^ 重心Gを中心とする拡大・縮小率 -+1/2 の相似変換 f により三角形ABCは三角形DEFに写され、垂心Hを中心とする拡大・縮小率 1/2 の相似変換 g により三角形ABCは三角形JKLに写されるから、外接円は相似変換 f および相似変換 g により九点円に写されるので、九点円の半径は外接円の半径 R の半分 R/2 である[3]。さらに、重心Gと垂心Hは相似の中心となり、外心を O、九点円の中心を N とすると、重心Gと垂心Hはオイラー線上で線分 ON をそれぞれ 2:1 に外分および内分するので、九点円の中心 N は外心 O と垂心 H の中点となる[3]。
- ^ 1990年バルト海団体数学コンテスト問8[9]
- ^ 垂心Hを中心とする拡大・縮小率 1/2 の相似変換 g により外接円は九点円に写されるから[10]。
- ^ 三角形ABCの内心Iは三角形IAIBICの垂心であり、三角形ABCの外接円は三角形IAIBICの九点円となるから[11]。
出典[編集]
参考文献[編集]
- 安藤哲哉『三角形と円の幾何学 数学オリンピック幾何問題完全攻略』海鳴社、2006年10月10日。ISBN 978-4-87525-234-4。
- H. S. M. コクセター 著、銀林浩 訳『幾何学入門』 上、筑摩書房〈ちくま学芸文庫 コ27-1 Math & Science〉、2009年9月10日。ISBN 978-4-480-09241-0。
- 高木貞治『近世数学史談・数学雑談』(復刻版)共立出版、1996年12月10日、88-90頁。ISBN 978-4-320-01551-7。 - 複素数を用いた九点円の定理の証明。
- Feuerbach, Karl Wilhelm; Buzengeiger, Carl Heribert Ignatz (1822), Eigenschaften einiger merkwürdigen Punkte des geradlinigen Dreiecks und mehrerer durch sie bestimmten Linien und Figuren. Eine analytisch-trigonometrische Abhandlung (Monograph ed.), Nürnberg: Wiessner. online book - Google ブックス
外部リンク[編集]
- 『九点円』 - コトバンク
- 『九点円の定理の証明と諸性質』 - 高校数学の美しい物語
- 『フォイエルバッハの定理と計算による証明』 - 高校数学の美しい物語
- Weisstein, Eric W. "Nine-Point Circle". mathworld.wolfram.com (英語).
- Weisstein, Eric W. "Feuerbach's Theorem". mathworld.wolfram.com (英語).
- History of the Nine Point Circle (英語)