ラグランジュ補間
数値解析におけるラグランジュ補間(ラグランジュほかん、英: Lagrange interpolation)は、多項式補間に用いられる。相異なる点の集合 xj および数値 yj に対し、そのラグランジュ補間多項式は、各 xj において対応する値として yj をとるような次数最小の多項式である。このように次数最小の多項式は一意に決まるが、決定する方法は複数存在するため、「ラグランジュ補間多項式」という名称をその一意な多項式の「ラグランジュ形」というふうに言及するのは正確でない。
名称はジョゼフ=ルイ・ラグランジュに因んだものだが、ラグランジュの発表する1795年よりも以前に、この方法を初めて発見したのは1779年のエドワード・ワーリングである。ラグランジュの結果はレオンハルト・オイラーが1783年に発表したより複雑な形の公式の簡単な帰結となるものであった[1]
ラグランジュ補間多項式は数値積分法の一種ニュートン–コーツ法でも用いられ、また有限体上で計算されたラグランジュ補間多項式は暗号理論におけるシャミアの秘密分散法でも用いられる。
ラグランジュ補間は巨大振幅に関するルンゲ現象の影響を受けやすい。また評価点 xj の変更に関して補間の計算を全くやり直す必要があるから、そのような目的では変更が容易にできるニュートン補間がしばしば用いられる。
定義[編集]
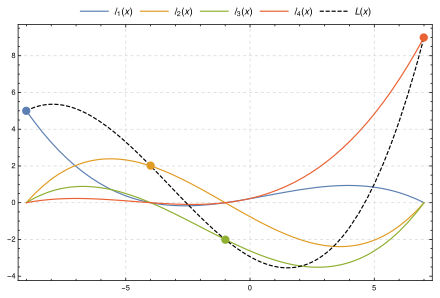
k + 1 個のデータ点集合 はどの二つの xj も同じでないとする。これらのデータのラグランジュ型の補間多項式とは、ラグランジュ基底多項式
まず最初の仮定により であるから、この式は常に矛盾なく定まる。 かつ となるような対を許さない理由は、必要な補間多項式 L () が存在しないからである(各引数 xi に対する値は一つでなければならない)。他方、 もそれら二点が実際には単一の点となる。
任意の i ≠ j に対して、基底多項式 ℓj(x) は分子に (x − xi) を因子として持つから、x = xi のとき積全体も零となる。他方、i = j のときは明らかに ℓi(xi) = 1 が成り立つ。すなわち、 である。ここに右辺はクロネッカーのデルタ。したがって各点 xi において となり L は所期の函数の補間を与えるものとなる。
注意[編集]

ラグランジュ型の補間では、多項式補間の線型性と補間多項式の一意性があるため、証明や理論的な議論では都合がよい。この一意性はヴァンデルモンド行列の可逆性(同じことだがヴァンデルモンド行列式が至る所消えないこと)からも導けることである。
しかしながら、構成からわかる通り、節点 xk を変更するごとに、ラグランジュ基底多項式をすべて計算し直さなければならない。そこで実用上(あるいは計算上)の目的では、重心形のラグランジュ補間(後述)やニュートン補間を用いるほうが良い。
等間隔に取った節点に関するラグランジュ補間やその他の補間は、真の函数の上下に振動する多項式を生じるものである。この振る舞いは節点の数を多くするにつれてルンゲ現象と呼ばれる発散に逢着しやすくなっていく。この問題は、補間に用いる点をチェビシェフ節点に選ぶことで解消できる[2]。
線型代数学的説明[編集]
補間問題を解くことは、逆行列を計算する線型代数学の問題につながる。標準的な単項式基底を用いた補間多項式 では、L(xi) = yi を L の係数 mj に関してヴァンデルモンド行列 を逆に解かなければならない。対して、ラグランジュ基底を用いて を作れば、この場合先ほどはヴァンデルモンド行列が現れた部分には単位行列 が現れ、逆行列は単位行列自身であるから、ラグランジュ基底は自動的に逆に解かれていることになる。
この構成は中国の剰余定理と類似対応している(つまり、素数を法とする整数の剰余を調べる代わりに、一次式を法とする多項式の剰余を見ている)。
重心形[編集]
ラグランジュ基底多項式を
この形の多項式補間を考えることの利点は、補間多項式 を評価するときに、重み wj が事前に分かっていれば、O(n) で計算できることである(ラグランジュ基底 ℓj(x) を個別に計算するのは O(n2) 掛かる)。もうひとつ重心形補間の利点として、新しい節点 xk+1 の追加も各 wj を で割って、新しい wj+1 を計算するだけで容易にできる点が挙げられる。
さらに第一形を単純化することもできて、まず定数函数 g(x) ≡ 1 の重心補間 を計算してから L を g で割れば、得られる
- は与えられた節点における補間性を失わない。この補間多項式を重心補間多項式の「第二形」あるいは「真の形」という。真の重心補間多項式は、L の各節点における評価に際してラグランジュ基底 ℓ を評価しなくてよいという点で有利である。
誤差項[編集]
与えられた函数 f を、節点 x0, …, xn において次数 n の多項式で補完するとき、誤差 は
この誤差項によって、誤差の範囲を
脚注[編集]
参考文献[編集]
- ^ Meijering, Erik (2002), “A chronology of interpolation: from ancient astronomy to modern signal and image processing”, Proceedings of the IEEE 90 (3): 319–342, doi:10.1109/5.993400.
- ^ Quarteroni, Alfio; Saleri, Fausto (2003), Scientific Computing with MATLAB, Texts in computational science and engineering, 2, Springer, p. 66, ISBN 9783540443636.
- ^ Jean-Paul Berrut & Lloyd N. Trefethen (2004). “Barycentric Lagrange Interpolation”. SIAM Review 46 (3): 501-517. doi:10.1137/S0036144502417715.
- ^ Abramowitz and Stegun, "Handbook of Mathematical Functions," p.878
関連項目[編集]
- ネヴィルのアルゴリズム
- ニュートン補間: ニュートン形の補間多項式
- バーンスタイン多項式: バーンスタイン形の補間多項式
- カールソンの定理
- ルベーグ定数 (補間法)
- Chebfun
- ニュートン級数の一覧
- フロベニウス共変行列
- シルベスターの公式: ラグランジュ–シルベスター補間
外部リンク[編集]
- 『ラグランジュの補間公式とその応用例』 - 高校数学の美しい物語
- Hazewinkel, Michiel, ed. (2001), “Lagrange interpolation formula”, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Weisstein, Eric W. "Lagrange Interpolating Polynomial". mathworld.wolfram.com (英語).
- Lagrange Interpolation Formula at ProofWiki
- Lagrange Polynomial Approximation at ProofWiki
- ALGLIB has an implementations in C++ / C# / VBA / Pascal.
- GSL has a polynomial interpolation code in C
- SO has a MATLAB example that demonstrates the algorithm and recreates the first image in this article
- Lagrange Method of Interpolation — Notes, PPT, Mathcad, Mathematica, MATLAB, Maple at Holistic Numerical Methods Institute
- Lagrange interpolation polynomial on www.math-linux.com
- Dynamic Lagrange interpolation with JSXGraph
- Numerical computing with functions: The Chebfun Project
- Worksheet Function for Bicubic Lagrange Interpolation
- Lagrange polynomials in Python















![{\displaystyle {\begin{aligned}\ell (x)&=(x-x_{0})(x-x_{1})\cdots (x-x_{k})\\[5pt]\ell '(x_{j})&={\frac {d\ell (x)}{dx}}{\Big |}_{x=x_{j}}=\prod _{i=0,i\neq j}^{k}(x_{j}-x_{i})\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82e60015b2a8ff4d783c14f0fa2000e25a33c786)








![{\displaystyle R(x)=f[x_{0},\ldots ,x_{n},x]\ell (x)=\ell (x){\frac {f^{(n+1)}(\xi )}{(n+1)!}},\quad \quad x_{0}<\xi <x_{n},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8bc32c3e9c3b1b357309a6ca9a7d9874d326690a)
![{\textstyle f[x_{0},\ldots ,x_{n},x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9429273fee3907bbb1b06a1953a8784f3b63cd7)

