| 形 |
図 |
 |
 |
面積
|
| 直角三角形
|
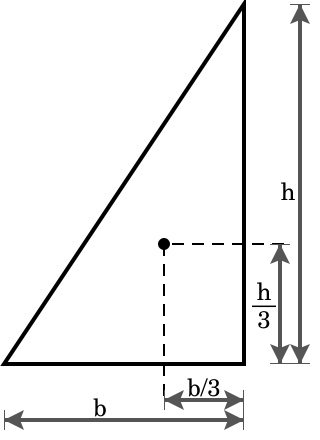
|

|

|

|
| 四分円
|

|

|

|

|
| 半円
|
半径  を持ち原点を中心とする円の、 を持ち原点を中心とする円の、 軸より上の領域 軸より上の領域
|

|

|

|
| 楕円の4分の1
|
楕円  のうち、第1象限にある領域 のうち、第1象限にある領域
|

|

|

|
| 楕円の半分
|
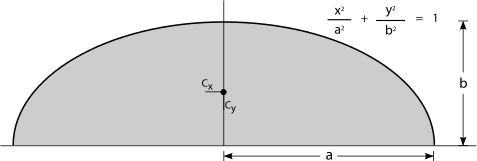
|

|

|

|
| 放物線の半分に囲まれた領域
|
放物線 と と  軸、直線 軸、直線 で囲まれた領域 で囲まれた領域
|

|

|

|
| 放物線
|
放物線 と 直線 と 直線 で囲まれた領域 で囲まれた領域
|

|

|

|
| 放物線の下部
|
放物線 と と  軸、直線 軸、直線 で囲まれた領域 で囲まれた領域
|

|

|

|
| 曲線の下部
|
曲線 と と  軸、直線 軸、直線 で囲まれた領域 で囲まれた領域
|

|

|

|
| 扇形
|
(極座標表記で) から から  の範囲内の 弧 の範囲内の 弧 と 弧の両端と原点を結ぶ直線で囲まれた範囲 と 弧の両端と原点を結ぶ直線で囲まれた範囲
|

|

|

|
| 弓形
|
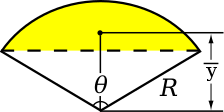
|

|

|

|
| 四分円の弧
|
 を満たす点のうち、第1象限にある部分 を満たす点のうち、第1象限にある部分
|

|

|

|
| 半円の弧
|
 を満たす点のうち を満たす点のうち  軸の上にある部分 軸の上にある部分
|

|

|

|
| 円弧
|
(極座標表記で)  かつ かつ  から から  の範囲にある部分 の範囲にある部分
|

|

|

|

















































