5項補題

数学、特にホモロジー代数学やアーベル圏の理論の応用において、5項補題（ごこうほだい、英: five lemma）、ファイブ・レンマは、可換図式についての重要で広く用いられる補題である。5項補題はアーベル圏だけでなく例えば群の圏においても成り立つ。

5項補題は2つの他の定理、four lemmas を合わせたものと考えることができる。この2つは互いに双対である。

ステートメント

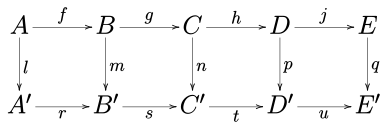
任意のアーベル圏（アーベル群の圏や与えられた体上のベクトル空間の圏など）や群の圏において以下の可換図式を考える。

5項補題は次のものである。2つの行が完全で、m と p が同型射で、i がエピ射で、q がモノ射であれば、n も同型射である。

2つの4項補題は以下のものである。
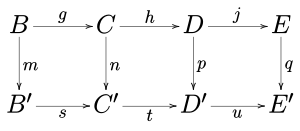
(1) 可換図式

の行が完全で m と p がエピ射で q がモノ射ならば、n はエピ射である。

(2) 可換図式

の行が完全で m と p がモノ射で l がエピ射ならば、 n はモノ射である。

証明

これから行う証明で使われる手法は一般に図式追跡 (diagram chasing) と呼ばれる。2つの4項補題を別々に証明することによって5項補題を証明する。

diagram chasing を行うために、ある環上の加群の圏において考える。そうすることで図式にある対象の元について話すことができ、図式の射をそれらの元に作用する関数（実際は準同型）と考えることができる。すると射がモノ射であることと単射であることは同値であり、エピ射であることと全射であることは同値である。同様にして、完全性を扱うために、通常の写像の意味で核と像を考えることができる。ミッチェルの埋め込み定理のおかげで、証明は任意の（小さい）アーベル圏にもなお適用することができる。これは任意の小さいアーベル圏はある環上の加群の圏として表現可能であるという定理である。群の圏に対しては、下記の加法的な表記を乗法的な表記に変えるだけでよい。可換性が全く使われないことに注意せよ。

さて、(1) を証明するために、m と p が全射で q が単射であると仮定する。

• c′ を C′ の元とする。
• p は全射なので、ある元 d ∈ D が存在して、p(d) = t(c′).
• 図式の可換性より、u(p(d)) = q(j(d)).
• 完全性より im t = ker u なので、0 = u(t(c′)) = u(p(d)) = q(j(d)).
• q は単射なので、j(d) = 0 であり、d は ker j = im h の元である。
• したがってある c ∈ C が存在して h(c) = d.
• すると t(n(c)) = p(h(c)) = t(c′) である。t は準同型なので、t(c′ − n(c)) = 0 である。
• 完全性より、c′ − n(c) は s の像に入っているので、ある b′ ∈ B′ が存在して、s(b′) = c′ − n(c).
• m は全射なので、ある b ∈ B が存在して、b′ = m(b).
• 可換性により、n(g(b)) = s(m(b)) = c' − n(c).
• n は準同型なので、n(g(b) + c) = n(g(b)) + n(c) = c′ − n(c) + n(c) = c′.
• したがって、n は全射である。

次に、(2) を証明するために、m と p が単射で l が全射と仮定する。

• c ∈ C を n(c) = 0 であるような元とする。
• すると t(n(c)) は 0 である。
• 可換性より、p(h(c)) = 0.
• p は単射なので、h(c) = 0.
• 完全性により、ある b ∈ B が存在して、g(b) = c.
• 可換性により、s(m(b)) = n(g(b)) = n(c) = 0.
• すると完全性により、ある元 a′ ∈ A′ が存在して、r(a′) = m(b).
• l は全射なので、a ∈ A が存在して、l(a) = a′.
• 可換性より、m(f(a)) = r(l(a)) = m(b).
• m は単射なので、f(a) = b.
• よって c = g(f(a)).
• g と f の合成は自明なので、c = 0.
• したがって n は単射である。

今2つの4項補題を合わせることで5項補題全体が証明される。

応用

5項補題はしばしば長完全列に適用される。与えられた対称のホモロジーやコホモロジーを計算するとき、大体はホモロジー／コホモロジーのわかっているより単純な部分対象を使って、もとの対象の、わかっていないホモロジー群を含む長完全列を得る。これだけではわかっていないホモロジー群を決定するには十分でないが、もとの対象と部分対象を射を通じてよくわかっている対象と比べれば、それぞれの長完全列の間の射が誘導され、したがって5項補題をわかっていないホモロジー群を決定するのに使うことができる。

関連項目

• 短5項補題、5項補題の特別な場合で、短完全列に対するもの
• 蛇の補題、diagram chasing によって証明できる別の補題
• 9項補題

参考文献

• W. R. Scott: Group Theory, Prentice Hall, 1964.
• Massey, William S. (1991), A basic course in algebraic topology, Graduate texts in mathematics, 127 (3rd ed.), Springer, ISBN 978-0-387-97430-9