ピンホールカメラモデル

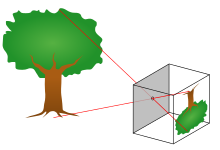
ピンホールカメラモデル（Pinhole_camera_model）では、 3次元空間内の点の座標と、理想的なピンホールカメラの画像平面への投影との間の数学的関係を記述する。

解説[編集]

ここで、カメラの開口部は点として記述され、光を集束させるためのレンズは使用しない。モデルには、たとえば、レンズや有限サイズのアパーチャーによって引き起こされる歪曲収差やぼやけは含まれない。また、ほとんどの実用的なカメラには離散的な画像座標しかないことも考慮しない。つまり、ピンホールカメラモデルは、 3次元シーンから2次元画像への写像の一次近似としてのみ使用できる。その有効性はカメラの品質に依存し、一般にレンズの歪みの影響が大きくなるにつれ、画像の中心から端に向かって減少する。

ピンホールカメラモデルが考慮していない効果の一部は、例えば画像座標に適切な座標変換を適用することにより補正できる。高品質なカメラが使用する場合、他の効果は無視できるほど小さい。これは、ピンホールカメラモデルが、たとえばコンピュータビジョンやコンピュータグラフィックスなどで、カメラが3Dシーンをどのように描写するかを合理的に説明するために使用できることを意味する。

幾何学[編集]

注: 図のx₁x₂x₃座標系は左手系です。つまり、OZ 軸の方向は、読者が慣れている座標系とは逆になっている。

ピンホールカメラの写像に関連する幾何学を図に示す。この図には、次の基本的なオブジェクトが含まれている。

Oを原点とする3次元直交座標系。Oは、カメラの開口部が配置されている場所でもある。座標系の3つの軸は、X1, X2, X3 と呼ばれる。軸X3はカメラの視線方向を指しており、光軸、主軸、または主光線と呼ばれる。軸X1とX2がまたがる平面は、カメラの前面、つまり主平面である。
カメラの開口部を通して3次元世界が投影される画像平面。像面はX1軸とX2軸に平行で、原点OからX3軸の負の方向に距離 $f$ 離れた位置にある。 $f$ はピンホールカメラの焦点距離である。ピンホールカメラの実際の実装では、画像平面がX3軸と座標- $f$ ( $f$ > 0 ) で交差するように配置される。
光軸と像面が交わる点R。この点は、主点^[1]または画像中心と呼ばれます。
3次元世界のどこかにある点P。軸X1, X2, X3に対して座標 $(x_{1},x_{2},x_{3})$ で表される。
点Pのカメラへの投影線。これは、点Pと点Oを通る緑色の線である。
Qで表される画像平面への点Pの投影。この点は、投影線（緑）と画像平面の交点によって与えられます。実際の状況では、 $x_{3}$ > 0 であれば交点が一意に定まると仮定できる。
画像平面も2次元座標系を持ち、原点はRで、軸Y1, Y2 はそれぞれX1, X2に平行である。この座標系に対する点Qの座標は、 $(y_{1},y_{2})$ となる。

すべての射影線が通過しなければならないカメラのピンホール開口は、無限に小さい点であると仮定される。文献では、3次元空間上のこの点は光学中心（またはレンズ中心またはカメラ中心）と呼ばれる。 ^[2]

定式化[編集]

次に、点Qの座標 $(y_{1},y_{2})$ が、点Pの座標 $(x_{1},x_{2},x_{3})$ にどのように依存するかを理解したい。これは、前の図と同じシーンを真上から、X2 軸の負の方向を見下ろしている次の図を使用して行うことができる。

この図には、2つの相似な三角形があり、どちらも射影線（緑）の一部を斜辺として持っている。左の三角形の隣辺は $-y_{1}$ $f$ 、右の三角形の隣辺は $x_{1}$ と $x_{3}$ である。2つの三角形は相似であるため、次のようになる。

{\frac {-y_{1}}{f}}={\frac {x_{1}}{x_{3}}}

もしくは

y_{1}=-{\frac {f\,x_{1}}{x_{3}}}

同様に、X1軸の負の方向を見ると、次が得られる。

{\frac {-y_{2}}{f}}={\frac {x_{2}}{x_{3}}}

もしくは

y_{2}=-{\frac {f\,x_{2}}{x_{3}}}

これは、点Pの3次元座標 $(x_{1},x_{2},x_{3})$ と画像平面上の点Qの画像座標 $(y_{1},y_{2})$ との関係式、

{\begin{pmatrix}y_{1}\\y_{2}\end{pmatrix}}=-{\frac {f}{x_{3}}}{\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}}

として要約できる。

回転像と虚像面[編集]

ピンホールカメラによって記述される3次元座標から2次元座標への変換は、透視投影とそれに続く画像平面での180°回転です。これは、実際のピンホールカメラの挙動（結果の画像が180°回転し、投影された物体の相対的なサイズは焦点までの距離に依存し、画像の全体的なサイズは画像平面と焦点の間の距離 $f$ に依存する）に対応している。我々がカメラに期待する回転していない画像を生成するには、次の2つの方法がある。

画像平面で座標系をいずれかの方向に180°回転させます。これは、実際にピンホールカメラを実装することで問題を解決する方法です。写真用カメラの場合、画像を見る前に画像を回転させます。デジタルカメラの場合、画像が回転する順序でピクセルを読み取る。
- $f$ ではなく $f$ でX3軸と交差するように画像平面を配置し、前述の計算をやり直す。これにより（実際には実装できない）虚像面が生成されるが、実際のカメラよりも分析が簡単な理論上のカメラが与えられる。

どちらの場合でも、3次元座標から2次元画像座標への変換は以下のように、上記の式からマイナスを除いた式となる。

{\begin{pmatrix}y_{1}\\y_{2}\end{pmatrix}}={\frac {f}{x_{3}}}{\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}}

同次座標[編集]

空間内の点の3次元座標から2次元画像座標への変換も、同次座標で表すことができる。 $\mathbf {x}$ を3次元点を表した同次座標（4次元ベクトル）とし、 $\mathbf {y}$ をその点をピンホールカメラで投影した点を表した同次座標（3次元ベクトル）とする。このとき、次の関係が成り立つ。

\mathbf {y} \sim \mathbf {C} \,\mathbf {x}

ここで $\mathbf {C}$ は $3\times 4$ のカメラ行列であり、記号 $\,\sim$ は、射影空間の要素が等しいことを意味する。これは、左辺と右辺が非ゼロのスカラー乗算に対して等しいことを意味します。この関係の帰結として、 $\mathbf {C}$ もまた射影空間の元と見なせる（2つのカメラ行列は、スカラー倍まで等しい場合は等価）。このピンホールカメラによる変換の記述は、2つの一次式の分数としてではなく、線形変換 $\mathbf {C}$ として、3次元座標と2次元座標間の関係の多くの導出を単純化することができる。^[要出典]

出典[編集]

^ Carlo Tomasi (2016年8月9日). “A Simple Camera Model”. cs.duke.edu. 2021年2月18日閲覧。
^ Andrea Fusiello (2005年12月27日). “Elements of Geometric Computer Vision”. Homepages.inf.ed.ac.uk. 2013年12月18日閲覧。

参考文献[編集]

David A. Forsyth and Jean Ponce (2003). Computer Vision, A Modern Approach. Prentice Hall. ISBN 0-12-379777-2
Richard Hartley and Andrew Zisserman (2003). Multiple View Geometry in computer vision. Cambridge University Press. ISBN 0-521-54051-8
Bernd Jähne (1997). Practical Handbook on Image Processing for Scientific Applications. CRC Press. ISBN 0-8493-8906-2
Linda G. Shapiro and George C. Stockman (2001). Computer Vision. Prentice Hall. ISBN 0-13-030796-3
Gang Xu and Zhengyou Zhang (1996). Epipolar geometry in Stereo, Motion and Object Recognition. Kluwer Academic Publishers. ISBN 0-7923-4199-6

[1] Carlo Tomasi (2016年8月9日). “A Simple Camera Model”. cs.duke.edu. 2021年2月18日閲覧。

[2] Andrea Fusiello (2005年12月27日). “Elements of Geometric Computer Vision”. Homepages.inf.ed.ac.uk. 2013年12月18日閲覧。

[1]

[2]