2元対称通信路
2元対称通信路(英: Binary symmetric channel、BSC)とは、符号理論や情報理論でよく使われる通信路モデルである。このモデルでは、送信者が1つのビット(0 か 1)を送信しようとし、受信者は1つのビットを受信しようとする。ビットは通常は正しく転送されるが、ある小さな確率(crossover probability)で反転したビットが受信されることがある。解析が最も容易な通信路であることから、情報理論で頻繁に使われる。
概要[編集]
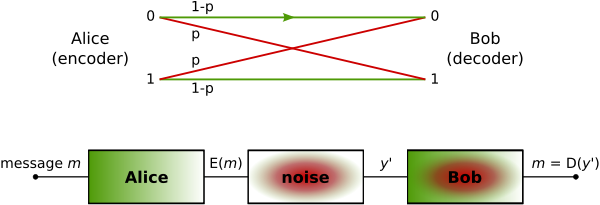
BSC は「2元通信路」である。つまり、2つの記号(一般に 0 と 1 とされる)のどちらかしか転送できない。非2元通信路は2種類以上の記号を転送可能である。その転送は完全ではなく、受信者は時折間違ったビットを受信してしまう。
この通信路は、ノイズのある通信路としては最も解析が容易であるため、理論研究でよく使われる。通信理論における様々な問題は BSC に還元できる。一方、BSC での効率的な転送が可能なら、もっと複雑な通信路にその方法を応用することができる。
定義[編集]
crossover probability(ビットが反転する確率)が p の2元対称通信路はバイナリ入力とバイナリ出力と誤り確率 p の通信路からなるとする。X を送信する確率変数、Y を受信する変数としたとき、この通信路の特性は次のような条件付き確率で表される。
- Pr( Y = 0 | X = 0) = 1-p
- Pr( Y = 0 | X = 1) = p
- Pr( Y = 1 | X = 0 ) = p
- Pr( Y = 1 | X = 1 ) = 1-p
ここでは、0 ≤ p ≤ 1/2 であると仮定している。p>1/2 だった場合は、受信者が受信結果を反転(1 だったら 0、0 だったら 1 とみなす)させれば、1-p ≤ 1/2 となる。
BSC の通信路容量[編集]
通信路容量は 1 - H(p) であり、H(p) は2値エントロピー関数である。
球充填の考え方により以下が示される。符号語を与えられたとき、典型集合の出力ビット列はおよそ 2 n H(p) となる。考えられる出力は全部で 2n であり、入力は 2nR の符号語から選ばれる。従って、受信者は考えられる出力それぞれについて、2n / 2nR = 2n(1-R) の球で空間の分割を決定できる。R> 1 - H(p) だった場合、球は詰め込みすぎとなって、受信者は出力から正しい符号語を特定できなくなる。
参考文献[編集]
- David J. C. MacKay. Information Theory, Inference, and Learning Algorithms Cambridge: Cambridge University Press, 2003. ISBN 0-521-64298-1
- Thomas M. Cover, Joy A. Thomas. Elements of information theory, 1st Edition. New York: Wiley-Interscience, 1991. ISBN 0-471-06259-6.
