ディフィー・ヘルマン鍵共有

ディフィー・ヘルマン鍵共有（Diffie-Hellman key exchange、デフィー・ヘルマンかぎきょうゆう）、あるいはディフィー・ヘルマン鍵交換（かぎこうかん）とは、事前の秘密の共有無しに、盗聴の可能性のある通信路を使って、暗号鍵の共有を可能にする暗号プロトコルである。この鍵は、共通鍵暗号方式の鍵として使用可能である。

概要

1976年にスタンフォード大学の2名の研究員ホイットフィールド・ディフィーとマーティン・ヘルマンは、公開鍵暗号の概念を提案し、その具体的な方式の一つとして、ディフィー・ヘルマン鍵共有（DH鍵共有）プロトコルを提案した。この鍵共有方式は共通鍵暗号方式における鍵の受け渡しを安全に行うために提案された方式である。

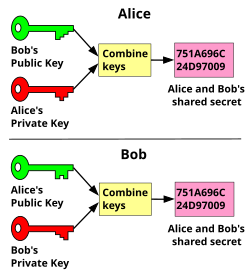
このプロトコルは、通信を行いたい2者が各々公開鍵と秘密鍵 (私有鍵ともいう) を用意し、公開鍵のみを公開する。そして、お互いに秘密の値から作成されるデータを相手に送信し、各自、自分の秘密鍵と受信したデータから共通鍵を作成できる方法である。第三者が送受信されるデータを盗聴しても鍵を生成することができない所に特徴がある。

アメリカ合衆国とカナダで特許が取得された。1997年4月29日に両国でアルゴリズムの特許期限が切れたため、現在では誰でも自由に利用できる。

プロトコルの内容

この方式は以下のように行われる。まず値の大きな素数 p を用意する。 また g を $({\Bbb Z}/p{\Bbb Z})^{\ast}$ の生成元とする。この g と p は公開されているものとする。

いま X と Y が通信を行うとする。このとき X と Y はお互い秘密の値 a , b を選択する、この値は 0 以上 p-2 以下の中からランダムに選ぶ。但し、ここで本当にゼロや小さな値（g^a < p となるa等）を選択すると安全性が損なわれる。

X は次の値 A を計算してこれを Y に送信する。

$A = g^a \mod p$

Y も同様に B を計算してこれを X に送信する。

$B = g^b \mod p$

X は自身の秘密の値 a と受信した B から以下の値を計算する。

$K_A = B^a \mod p$

Y も自身の秘密の値 b と受信した A から以下の値を計算する。

$K_B = A^b \mod p$

このとき X と Y が計算した K は共に

$K_A = K_B = g^{ab} \mod p$

になっているため、以後この値を共通鍵暗号方式の鍵として使用する。

ここで第三者 Z がこの二人の通信を盗聴して A と B を入手しても、 $A = g^a \mod p$ と $B = g^b \mod p$ から $K = g^{ab} \mod p$ を多項式時間で計算する方法は現在の所、存在しないので Z は鍵 K を生成することが困難である。このため　X と Y が安全に通信を行うことが可能になる。

中間者攻撃

ディフィー・ヘルマン鍵共有自体は認証手段を提供するものではないため、単独では中間者攻撃に対して脆弱である。

ここではディフィー・ヘルマン鍵共有における中間者攻撃の具体的な手順について示す。

DNS偽装・ARPスプーフィング・その他の手段により攻撃者 Z がこの二人の通信を中継して A と B を入手したとする。

このとき Z はそれらに対して秘密の値 c と d を選択する。この値は a や b と同じ基準で選択される。

Z は c を用いて次の値を計算して Y に送信する。

$A_z = g^c \mod p$

また d を用いて計算して X に送信する。

$B_z = g^d \mod p$

Y は自身の秘密の値 b と受信した値から以下の値を計算する。

$K_{BZ} = A_z^b \mod p$

X は自身の秘密の値 a と受信した値から以下の値を計算する。

$K_{AZ} = B_z^a \mod p$

Z は自身の秘密の値 c と d と受信した A と B から以下の値を計算する。

$K_{ZAZ} = A^d \mod p$

$K_{ZBZ} = B^c \mod p$

このとき X と Y と Z が計算した K は共に

$K_{AZ} = K_{ZAZ} = g^{ad} \mod p$

$K_{BZ} = K_{ZBZ} = g^{bc} \mod p$

になっている。

以降の通信で Z はこれらの値を共通鍵暗号方式の鍵として使用して X と Y の通信を中継し、盗聴や改ざんを行う。

参考文献

• W. Diffie and M. E. Hellman, "New Directions in Cryptography", IEEE Transactions on Information Theory, vol.IT-22, No.6, pp.644-654, Nov, 1976.
• カナダの特許1,121,480

関連項目

• 暗号理論