Template:NumBlk
このテンプレートは、数式などによく用いられる、番号付きのブロック (Numbered Block) を生成します。このテンプレートは {{EquationRef}} と併用することができ、番号付きの数式に参照リンクをつけることができます。こうすることで、{{EquationRef}} で与えた参照 id を通じて本文中に書かれた {{EquationNote}} から目的の数式へジャンプできるようになります。
引数
引数 {{{1}}}, {{{2}}}, {{{3}}} はテンプレートを使用する際に必須です。さらに、オプションの引数として {{{RawN}}}, {{{LnSty}}} と、試験的に {{{Border}}} が用意されています。
| 引数 | 指定内容 | 既定値 | 説明 |
|---|---|---|---|
| {{{1}}} | インデントのレベルを指定。コロン (:) を入れた数だけインデントされる(最大 20 レベル)。 | ||
| {{{2}}} | ブロックの本体(主に数式)。 | ||
| {{{3}}} | ブロックの番号(主に式番号)。 | ||
| {{{RawN}}} | 空要素や空白文字でない値を代入した場合、ブロック番号の周りの括弧が取り除かれる(RawN の値を明示しない場合、ブロック番号が丸括弧で括られる)。 | ||
| {{{LnSty}}} | 本体と番号を結ぶ線のスタイルを指定(デフォルトでは線なし)。 | ||
| {{{Border}}} | ブロックを枠線で囲む(試験中)。 |
例
数式の出力 | |
|---|---|
|
|
(Eq. 3) |
|
|
(Eq. 3) |
|
|
(2) |
インデント | |
|
|
(3.5) |
|
|
(1) |
|
|
(13.7) |
|
|
(1.2) |
式番号のフォーマット | |
|
|
3.5 |
|
|
<3.5> |
|
|
[3.5] |
|
|
[3.5] |
|
|
([3.5]) |
|
|
[3.5] |
|
|
|
線のスタイル | |
|
|
(3.5) |
|
|
(3.5) |
|
|
[3.5] |
|
|
[3.5] |
|
|
[3.5] |
|
|
[3.5] |
|
|
[3.5] |
枠線 | |
|
|
(Eq. 3) |
画像との相対的な配置
番号付きブロックは可能ならばディスプレイ上で画像の左側か右側に回りこんで配置されるようになっています。もし一行全部を使って番号付きブロックを表示させたい場合には、{{clear}} などのテンプレートを使うことを検討して下さい。
- 回り込みと {{clear}} の使用例:
[[Image:Bnet_fan2.png|frame|right|図 1. ベイジアンネットワークによる Eq.(6) の表現]]
[[Image:Bnet_fan2.png|frame|left|図 1. ベイジアンネットワークによる Eq.(6) の表現]]
<br><br>ベイジアンネットワーク(または信念ネットワーク)は確率的なグラフ・モデルであり、
変数の組とそれらの確率的な独立性とをグラフによって表現する。例えば、ベイジアンネットワークは
種々の病気とその徴候との間の確率的な関係を表現できる。与えられたいくつかの徴候から、
ネットワークを用いて様々な病気の存在確率を計算することができる。
{{NumBlk|1=:|2=<math>
P(a, b, \lambda) = P(a| \lambda) P(b | \lambda) P(\lambda)\,
</math>,|3='''Eq.(6)'''|RawN=.}}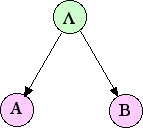

ベイジアンネットワーク(または信念ネットワーク)は確率的なグラフ・モデルであり、
変数の組とそれらの確率的な独立性とをグラフによって表現する。例えば、ベイジアンネットワークは
種々の病気とその徴候との間の確率的な関係を表現できる。与えられたいくつかの徴候から、
ネットワークを用いて様々な病気の存在確率を計算することができる。
- もし番号付きブロックを横幅一杯に表示させたい場合、ブロックの手前に {{clear}} を置きます。
[[Image:Bnet_fan2.png|frame|right|図 1. ベイジアンネットワークによる Eq.(6) の表現]]
[[Image:Bnet_fan2.png|frame|left|図 1. ベイジアンネットワークによる Eq.(6) の表現]]
<br><br>ベイジアンネットワーク(または信念ネットワーク)は確率的なグラフ・モデルであり、
変数の組とそれらの確率的な独立性とをグラフによって表現する。例えば、ベイジアンネットワークは
種々の病気とその徴候との間の確率的な関係を表現できる。与えられたいくつかの徴候から、
ネットワークを用いて様々な病気の存在確率を計算することができる。
{{clear}}
{{NumBlk|1=:|2=<math>
P(a, b, \lambda) = P(a| \lambda) P(b | \lambda) P(\lambda)\,
</math>,|3='''Eq.(6)'''|RawN=.}}

ベイジアンネットワーク(または信念ネットワーク)は確率的なグラフ・モデルであり、
変数の組とそれらの確率的な独立性とをグラフによって表現する。例えば、ベイジアンネットワークは
種々の病気とその徴候との間の確率的な関係を表現できる。与えられたいくつかの徴候から、
ネットワークを用いて様々な病気の存在確率を計算することができる。
カテゴリ
このテンプレートが貼り付けられたページに適用するカテゴリはありません。






