二項ヒープ
二項ヒープ(にこうヒープ、binomial heap)とは、計算機科学におけるデータ構造(ヒープ)の1つである。特徴は以下の通り。
- 二分ヒープとよく似たデータ構造であるが、二項ヒープは2つのヒープを素早くマージする操作をサポートしている。
- 特殊な木構造を用いることで実現される。
- マージ可能な抽象データ型ヒープ(meldableヒープとも呼ばれる)の実装として重要。
二項木[編集]
二項ヒープは二項木の集合として実装される(二分ヒープと比較すると、二分ヒープは単一の二分木から構成される)。二項木は再帰的に定義される。

次数 k の二項木はのノードを持ち、高さはk である。
その構造の特有さから、マージ操作は簡単に行うことができる。 例えば、次数 k の二項木を作るには、次のようにする。
- 次数 k-1の2つの木 と があるとする。
- (または ) の一番左の子として、 (または )を付け加える。
この特徴は二項ヒープのマージ操作の中核を成すものであり、従来のヒープに優る大きな利点となっている。
二項ヒープの構造[編集]
二項ヒープは、以下の2つの性質を満たす二項木の組で実装される。
- ヒープ内のそれぞれの二項木は、「ノードのキーはその親のキーよりも大きいか等しい」という最小ヒープの特性に従う。
- 二項木は次数 0を含む各々の次数について、ただ1つ存在、あるいは存在しないかのいずれかである。
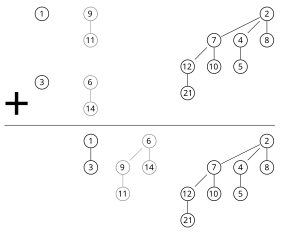
第1の特徴は、それぞれの二項木の根は、1つの木の中に最小のキーを持つことを保証している。これはヒープ全体に当てはまる。 第2の特徴は、n個の要素を持つ二項ヒープは高々 log(n + 1) の二項ヒープから構成されていることを意味する。実際、これらの木の数字と順番はn要素の数字によって一意に決定される。それぞれの二項木はnの2進表現の1に一致する。例えば、13という数は2進数では「1101」であり、と表現される。つまり、13個の要素を持つ二項ヒープは次数 3、2、0の3つの二項木から構成される(下図参照)。

実装[編集]
二項木たちの根へのランダムアクセスを要求する操作は無いので、二項木たちの根は連結リストに木の次数の昇順に格納できる。
マージ[編集]
上で述べたように、最も単純かつ重要な操作は二つの二項ヒープ内で同じ次数の2つの二項木をマージすることである。二項木の構造からそれは簡単にマージできる。木の中では根は最も小さい要素なので、二つのキーを比較することにより、二つの根の小さいほうが最小のキーになるので、それが新しい根になる。そして、もう一方の木はマージ後の木の部分木となる。この操作は二つの二項ヒープを完全にマージする最も基本的なものである。
function mergeTree(p, q)
if p.root <= q.root
return p.addSubTree(q)
else
return q.addSubTree(p)

二つのヒープをマージする操作は、他のほとんどの操作においてサブルーチンとして使われる。両方のヒープの根のリストは同時に検査される。これはマージアルゴリズムに似ている。もし、次数 jの木を含んでいるヒープが唯一つだけあるならば、その木はマージされたヒープに移動される。もし、2つのヒープが次数 jの木を含んでいるならば、最小ヒープ特性を満足させるために、二つの木はマージされ次数 j+1の一つの木となる。もしかしたらその後、その木はどちらかのヒープ内の次数 j+1の木とマージする必要が発生するかもしれない。このアルゴリズムの実行中、それぞれの次数について多くとも3つの木を試験する必要がある。(マージする二つのヒープからの二つの木と二つのより小さい木から成る一つの木の計3つ)。それぞれの木の次数は最大でlog2 nであり、それゆえにマージにかかる時間はO(log n)になる。
function merge(p, q)
while not( p.end() and q.end() )
tree = mergeTree(p.currentTree(), q.currentTree())
if not heap.currentTree().empty()
tree = mergeTree(tree, heap.currentTree())
heap.addTree(tree)
else
heap.addTree(tree)
heap.next() p.next() q.next()
挿入[編集]
ヒープに新しい要素を挿入する操作は、単に挿入する要素のみを含んだ新しいヒープを作成しそれを既存のヒープとマージさせるだけで完了する。実行時間はO(log n)かかる。
最小値検索[編集]
ヒープの最小要素を見つけるには、ただ二項木たちの根の中で最小のものを見つけるだけでよい。この処理は O(log n)時間内にたやすく完了できる。
最小要素を含む二項木を指すポインタを使うことによって、この操作にかかる時間をO(1)にまで減らすことができる。そのポインタは最小要素検索以外の任意の操作を行うときにおいても必ず更新しなければならない。この操作は、任意の操作を行う時間とは別にO(log n)時間内に完了する。
最小値削除[編集]
ヒープから最小値要素を削除するには、まずはじめに削除する要素を検索し、二項木からその要素を削除し、その要素を削除した二項木の部分木のリストを得る。その際に、分離された二項ヒープ内にある部分木のリストを大きい順に並べ替える。そしてそのヒープと元のヒープをマージする。
キー値減算[編集]
ある要素のキー値を減らした後、そのキーの親よりもキー値が小さくなったならば、最小ヒープの特性に違反してしまう。この場合、その親の要素と交換し、必要ならばさらにその親とも交換し、最小ヒープの特性には違反しなくなるまで続ける。それぞれの二項木の高さは高々log2 nであり、この処理にはO(log n)の時間かかる。
削除[編集]
ヒープからある要素を削除するには、そのキー値を負の無限大へ減算し(あるいは、ヒープ内の任意の要素よりも小さい値へ減算し)、ヒープ内の最小値を削除する。
パフォーマンス[編集]
n 個の要素を持つ二項ヒープに対して、以下の全操作の計算量はO(log n)である。
- ヒープに新しい要素を挿入する
- 最小のキーを持つ要素を検索する
- ヒープから最小のキーを持つ要素を削除する
- 指定された要素のキー値を減算する
- ヒープから特定の要素を削除する
- 二つの任意のヒープを一つのヒープにマージする
最小のキーを持つ要素の検索は、最小キーへのポインタを追加し利用することで、O(1)で実行できる。
派生[編集]
二項ヒープの派生は、フィボナッチヒープやソフトヒープのような他の似たようなヒープデータ構造を構築するのに用いられている。
関連項目[編集]
外部リンク[編集]
 ウィキメディア・コモンズには、二項ヒープに関するカテゴリがあります。
ウィキメディア・コモンズには、二項ヒープに関するカテゴリがあります。




