
 の漸近線は y 軸と直線 y = x である。
の漸近線は y 軸と直線 y = x である。
漸近線(ぜんきんせん、asymptote)とは、ある曲線と原点から十分遠いところで近づき、接することのない直線のことである。直線でなく一般に曲線とすることもある。漸近線は存在するとは限らず、複数存在する場合もある。漸近線を見出すことは、曲線のグラフの概形をつかむ一助となる。特に平面においては、曲線の遠くでの存在範囲を直線領域内としてとらえることができる。平面座標における関数のグラフの漸近線の方程式は、比較的求めやすい。
例
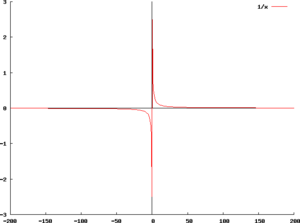 y = 1/x のグラフの漸近線は、x 軸および y 軸である。
y = 1/x のグラフの漸近線は、x 軸および y 軸である。
 曲線が漸近線と無限回交わる例
曲線が漸近線と無限回交わる例
整関数のグラフには、漸近線は存在しない。
漸近線が存在する最も簡単な例として、関数 y = 1/x が挙げられる。このグラフの漸近線は、直線 x = 0 と直線 y = 0 である。y = 1/x のグラフを描くことで、どの端もこれらの直線に近づいていき、また接しないことが見てとれるだろう。漸近線が存在する関数は他にも多く存在する。代表的なものとして、以下が挙げられる。
- 正接関数
- y = tan x(漸近線は x = π/2 + nπ(n は整数))
- 指数関数
- y = ax(a > 0, a ≠ 1)(漸近線は y = 0)
- 対数関数
- y = loga x(a > 0, a ≠ 1)(漸近線は y = 0)
- 双曲線
 (a > 0, b > 0)(漸近線は
(a > 0, b > 0)(漸近線は  )(複号任意)
)(複号任意)- 双曲線正接関数
 (漸近線は y = ± 1)
(漸近線は y = ± 1)- 逆正接関数
 (漸近線は
(漸近線は  )
)- 逆双曲線正接関数
 (漸近線は x = ± 1)
(漸近線は x = ± 1)
分数関数においては、漸近線が存在する事例が多いが、存在しないこともある。(存在しない例: )
)
グラフと漸近線が遠くで無限回交わる例もある。減衰曲線と x 軸はその一例である。(例: や y = e− xsin x など)
や y = e− xsin x など)
漸近線の方程式の求め方
関数のグラフ
前述したように、座標平面の関数のグラフの漸近線の方程式は比較的容易に求めることができる。漸近線は直線なので、関数 y = f(x) の漸近線は
- x = a(y軸に平行)
- y = ax + b
の2タイプに分けられる。
y 軸に平行な漸近線
直線 x = a がグラフ y = f(x) の漸近線であるための必要十分条件は、以下の4つのいずれかを満たすことである。




漸近線 x = a への近づき方は、直線 x = a の右または左から、上方向または下方向へ近づく4タイプが考えられるからである。
4条件いずれの場合においても、f(x) は x = a で不連続である。したがって、関数の不連続点を調べていけばよい。
1次関数である漸近線
直線 y = ax + b がグラフ y = f(x) の漸近線であるとする。近づく場所は x → ∞ または x → − ∞ のところである。x → ∞ で近づくとする。このとき漸近線 y = ax + b の傾き a, y 切片 b は次の極限値で与えられる。


(証明)
直線 y = ax + b がグラフ y = f(x) の漸近線なので、直線 y = ax + b はグラフ y = f(x) に近づく。今、近づく場所を x → ∞ と仮定しているので、

左辺の関数式を x で割ったものは、x → ∞ のとき尚のこと 0 に収束していく。したがって

左辺の関数式を分配すると、 なので、
なので、

ゆえに  となる。
となる。
 については、
については、 から明らかに導かれる。■
から明らかに導かれる。■
x → − ∞ で近づく場合も同様である。∞ を − ∞ に代えればよい。
1次関数である漸近線は、x → ∞ の方向と x → − ∞ の方向に存在するとしてもそれぞれ高々1つであることが分かる。
水平な漸近線
上の式の特に a = 0 の場合である、水平な漸近線は比較的求めやすい。直線 y = b がグラフ y = f(x) の漸近線であるならば、
 または
または 
である。
 y = arctan x のグラフは、2つの水平な漸近線が存在する例である。
y = arctan x のグラフは、2つの水平な漸近線が存在する例である。
例えば、逆正接関数 y = arctan x において、


であるので、 が漸近線である。
が漸近線である。
分数関数の漸近線
分数関数においては、上記のような方法を使わずに求めることができる。
分数関数の方程式を  (
( ,
,  は整式,
は整式,  は定数関数でない)とする。
は定数関数でない)とする。
h(x) = 0, g(x) ≠ 0 となる x を a1, ... , an とすると、y 軸平行な漸近線は直線 x = a1, ... , x = an となる。
例えば、

の y 軸平行な漸近線は直線 x = 0, x = 1 である。直線 x = 2 は漸近線でない。
次に、1次関数である漸近線について。
g(x) ÷ h(x) の商,余りをそれぞれ q(x), r(x) (deg r < deg g) とする。このとき

である。deg g − deg h の場合に応じて、1次関数の漸近線は次の表のようになる。
分数関数の1次関数型漸近線リスト
| deg g − deg h
|
1次関数型漸近線
|
分数関数,1次関数型漸近線の例
|
| < 0
|
y = 0
|

|
| = 0
|
y = q(x)(定数関数)
|

|
| = 1
|
y = q(x)
|

|
| > 1
|
存在しない
|
 , なし , なし
|
いずれも  であることを確かめることにより得られる。
であることを確かめることにより得られる。
曲線である漸近線
 x2 + 2x + 3 は(x3 + 2x2 + 3x + 4)/x の方物線型漸近線である。
x2 + 2x + 3 は(x3 + 2x2 + 3x + 4)/x の方物線型漸近線である。
漸近線は直線であることを普通仮定するが、曲線によっては曲線である漸近線を考えると形をとらえやすいことがある。
例えば、

は、 を補助にとるととらえやすくなる。
を補助にとるととらえやすくなる。








































