リカレンスプロット
リカレンスプロット(Recurrence plot)とは、時系列データを表現する方法の一つとして統計やカオス理論において用いられるモノクロ二次元の図である。時系列の各点について、値がほぼ等しくなる時間を点としてプロットして作られる。生命科学分野ではコンタクトマップとも呼ばれる。
詳細
[編集]リカレンスとは回帰という意味であり、以前の値へと戻ってくる性質を表す。リカレンスプロットは時系列の周期性に着目し、 を位相空間内の軌跡としたとき、の場合にのみ座標 に点が描画された対称行列を図示したものである。点が描画される値の近さをリカレンススレートと呼び、
とし、 が の場合のみ(黒い)点を描画することでリカレンスプロットを描画する。
周期性や繰り返しを示す自然のプロセスは多く、季節やミランコビッチ・サイクルのような明確な周期性だけでなく、エルニーニョ・南方振動のような不規則な周期性も存在する。観測された時系列が周期性をもつ場合、その背後に何らかの状態が繰り返すこと、すなわち状態が遷移した後に再び近い値に戻ってくる性質があることが想定される。こうした状態の回帰性は、決定論的な力学系の基本特性だけでなく、非線形・カオス系の性質としてもよく見られる(ポアンカレの回帰定理を参照)。自然界における繰り返しは、1890年にアンリ・ポアンカレが研究するなど、古くから知られている。
1987年に Eckmann らは位相空間内の軌跡の周期的な性質を視覚化するためにリカレンスプロットを導入した。位相空間は一般に高次である場合もあるが、リカレンスプロットでは低い次元(主に2次元)の位相空間に射影され、さらにバイナリー表現されることで情報が削減される。しかし、リカレンスプロットは2次元平面に描画される図であるにもかかわらず、m次元位相空間における特定の様相(特に周期性)をうまく表現する。例えば、時系列の値が厳密に周期 を持つならば、そのような時間のペア全体は の倍数ごとに分けられて、対角線(と並行な線)として描かれる。実際には、連続の値は計測時に標本化・量子化が行われるため、値が十分近い値になった場合にペアを描画する。
値の性質によって、リカレンスプロットに単一の点・対角線・垂直/水平線などの構造が見られる。そのような texture と呼ばれる大規模な構造は、均一、周期的、ドリフト・無秩序などに分けられる。この視覚に訴える外観が、その値が従う系についてのヒントになりうる。
一方で、リカレンスプロットの小規模な構造は、再帰定量分析に使用される (Zbilut & webber (1992), Marwan et al. (2002))。この定量化によって、リカレンスプロットを定量的に記述し、系の遷移や非線形パラメータの解析に用いることが可能になった。再帰定量分析のヒューリスティックな手法が埋め込みパラメータの選択に依存するのとは対照的に、埋め込みパラメータに依存しない相関次元、K2エントロピー、相互情報量もリカレンスプロットから導出可能である。これらの値は基本的に対角線の長さの分布と関係する。リカレンスプロットの利点は、短いデータや非定常データに対しても有用な結果を得られる点であるが、十分に長いリカレンスプロットであればリカレンスプロットだけから元の時系列を復元できることも数学的に証明されており[1]、多次元尺度構成法をつかった具体的な方法も示されている。この点でリカレンスプロットは時系列の情報をよく含んでいることが示唆される。
リカレンスプロットの各行または各列はバイナリ表現された一次元の点列であり、これは一つの記号に対応付けることができる。このことからリカレンスプロットは時系列を文字列に変換する手法でもある。また時系列の各点をノードと見立て、近接する点をリンクがあるとみなすことで、リカレンスプロットが時系列をグラフ表現したものであるとみなすこともできる。こうしてリカレンスプロットを経由して時系列を、対応する他の情報表現に変換することが、最近研究されている。
拡張
[編集]- Unthreshold recurrence plotは点同士の距離を計算したのち離散化しないで表現したプロットである。
- Close returns plotはリカレンスプロットに似ており、リカレンスプロットが絶対時間を 軸とする代わりに、close returns plot は相対時間を 軸とする図である。
- クロスリカレンスプロット (Marwan & Kurths (2002)) は、同じ位相空間の異なる値を考慮するものであり、2つの系とに対して
である。 2つのデータの次元は等しい必要があるが、データ長は異なっていても描画可能である。クロスリカレンスプロットは、2つの系の状態が類似する頻度を比較する。2つの系で類似したパターンを探すためや、時間スケールの異なる2つの系の時間の関係の研究のために用いることが可能である (Marwan & Knuths (2005))。
- ジョイントリカレンスプロットは、下位系(サブシステム)を考慮した、リカレンスプロットのアダマール積である (Romano et al. (2004))。2つの系とに対して、ジョイントリカレンスプロットは
となる。クロスリカレンスプロットとは対照的に、ジョイントリカレンスプロットは2つ(以上)の系における周期の同時発生を比較する。さらに、考慮する状態の数が等しければ系の次元が異なっていても比較可能である。ジョイントリカレンスプロットは位相の同期を検出するために用いられる。
例
[編集]
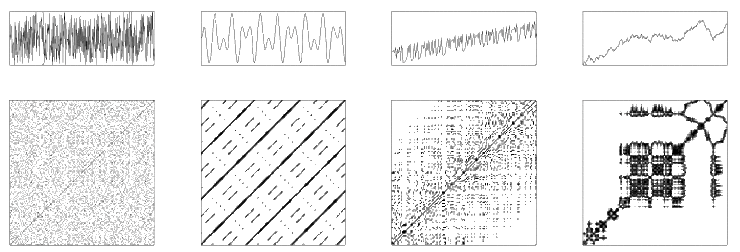
参照
[編集]- ポアンカレプロット
- Recurrence period density entropy:決定論的・確率論的な動的システムの再帰特性の要約に用いられる情報論的方法
- 再帰定量分析:リカレンスプロットを定量化するヒューリスティックな手法
- 自己相似性マトリクス
脚注
[編集]- ^ Hirata, Y., Komuro, M., Horai, S. and Aihara, K.: Faithfulness of recurrence plots: a mathematical proof, International Journal of Bifurcation and Chaos, Vol. 25, No. 12, p.1550168 (2015).
参考文献
[編集]- J. P. Eckmann, S. O. Kamphorst, D. Ruelle (1987). “Recurrence Plots of Dynamical Systems”. Europhysics Letters 5 (9): 973–977. Bibcode: 1987EL......4..973E. doi:10.1209/0295-5075/4/9/004.
- N. Marwan (2007). “Recurrence Plots for the Analysis of Complex Systems”. Physics Reports 438 (5-6): 237. Bibcode: 2007PhR...438..237M. doi:10.1016/j.physrep.2006.11.001.
- N. Marwan (2008). “A historical review of recurrence plots”. European Physical Journal ST 164 (1): 3–12. Bibcode: 2008EPJST.164....3M. doi:10.1140/epjst/e2008-00829-1.












