ドロネー図
この記事で示されている出典について、該当する記述が具体的にその文献の何ページあるいはどの章節にあるのか、特定が求められています。 |
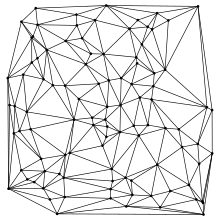
ドロネー図(ドロネーず、英語: Delaunay diagram)あるいはドロネー三角形分割(ドロネーさんかっけいぶんかつ、露: триангуляция Делоне, 英: Delaunay triangulation)は、距離空間内に離散的に分布した点の集合に対し得られる、それらをある方法に従い辺で結んだ図形である。
計算幾何学あるいは離散幾何学における代表的な考察対象の1つである。名称は考案者であるロシアの数学者、ボリス・ドロネー(露: Борис Николаевич Делоне)に由来する。ドロネー図の双対はボロノイ図であり、ドロネー図はボロノイ領域の隣接関係を表している。
双対[編集]
与えられたボロノイ図から対応するドロネー図を作図するには、与えられたボロノイ図の各領域(ボロノイ領域)に一つずつの特定の点(母点)を選んで固定し、どの二つのボロノイ領域についても、それが隣接ボロノイ領域ならば母点同士を結び、隣接していない場合は二つの母点を結ばないという操作を行う。元のボロノイ図の母点をドロネー点、得られたドロネー図のドロネー点を結んでいる線分をドロネー辺あるいはドロネー境界という。二次元のドロネー図ならば、ドロネー点とドロネー辺は多角形(ドロネー多角形)をつくるが、特殊な場合を除きこの多角形は三角形となり(退化して三角形とならない場合には母点を取り替えることで解消できる)、平面はドロネー図によってドロネー三角形の集まりに分割される。これをドロネー三角形分割という。次元を上げても同様のこと(ドロネー単体分割)を考察することができる。
関連項目[編集]
参考文献[編集]
英文[編集]
- Shewchuk, J.; Dey, T. K.; Cheng, S. W. (2016) (英語). Delaunay mesh generation. Chapman and Hall/CRC. ISBN 9781584887317
- Si, Hang (2015). “TetGen, a Delaunay-based quality tetrahedral mesh generator” (英語). ACM Transactions on Mathematical Software (TOMS) 41 (2): 1-36. ISSN 0098-3500.
- Du, Q.; Wang, D. (2006). “Recent progress in robust and quality Delaunay mesh generation.” (英語). en:Journal of Computational and Applied Mathematics 195 (1-2): 8-23. ISSN 0377-0427..
- Shewchuk, J. R. (2002) (英語). Delaunay refinement algorithms for triangular mesh generation. 22. pp. 21-74. ISSN 0925-7721.
- Shewchuk, Jonathan Richard (1997). “Delaunay refinement mesh generation” (英語). Carnegie-Mellon Univ Pittsburgh Pa School of Computer Science, Ph.D. Thesis.. Research paper (Carnegie Mellon University. School of Computer Science), CMU-CS-97-137.. OCLC 37586603.
和文[編集]
- 杉原厚吉『計算幾何学』朝倉書店〈数理工学ライブラリー, 1〉、2013年。ISBN 9784254116816。
- 浅野哲夫『計算幾何: 理論の基礎から実装まで』共立出版、2007年。ISBN 9784320121768。
- 杉原厚吉『FORTRAN 計算幾何プログラミング』岩波書店〈岩波コンピュータサイエンス〉、1998年3月20日。ISBN 4000077082。
