マルコフ決定過程

マルコフ決定過程 (Markov Decision Process; MDP) は結果が部分的にランダムかつ部分的に意思決定者による制御をおこなう状況でえられる場合における意思決定のモデリングにおける数学的枠組みを与える．MDP は動的計画法や強化学習などを用いて解かれる幅広い最適化問題の研究において有益である．MDP は少なくとも1950年代には知られていた (Bellman 1957）が，研究の中核は1960年に出版された ロナルド-A-ハワード" の "Dynamic Programming and Markov Processes" に起因する[1]。MDP はロボット工学，制御工学(automated control)、 経済学、 製造業を含む幅広い分野で用いられている。

概要

より正確には、マルコフ決定過程は離散時間の確率制御過程 (discrete time stochastic control process) である。各時刻において過程 (process) は 状態 ${\textstyle s}$ を取り，意思決定者は状態 ${\textstyle s}$ において利用可能な行動 ${\textstyle a}$ を任意に選択する。過程は次の時刻においてランダムに新しい状態 ${\textstyle s'}$ に移動し，意思決定者に対応する報酬 ${\textstyle R_{a}(s,s')}$ を与える。

過程が新しい状態 ${\textstyle s'}$ に遷移する確率は選択された行動の影響を受ける．具体的には，状態遷移関数 $P_{a}(s,s')=\Pr(s_{t+1}=s'\mid s_{t}=s,a_{t}=a)$ で与えられる．すなわち，次の状態 $s'$ は現在の状態 ${\textstyle s}$ と行動 ${\textstyle a}$ に依存するが， ${\textstyle s}$ と ${\textstyle a}$ が与えられたもとで過去の状態および行動と条件付き独立となる．言い換えると，マルコフ決定過程の状態遷移はマルコフ性を満たす．

マルコフ決定過程はマルコフ連鎖の拡張である．違いは（選択可能な）行動，および（モチベーションを与える）報酬を追加したことである．逆に言えば，各状態に対し（"wait"など）一意の行動が存在し，その際に得られる報酬が同じであれば，マルコフ決定過程はマルコフ連鎖に置き換えられる。

定義

3つの状態と2つの行動をもつ簡単な MDP の例

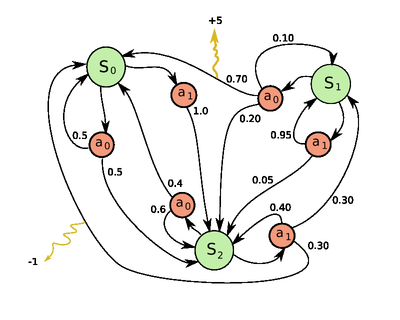
マルコフ決定過程は4つの要素の組 $(S,A,P_{\cdot }(\cdot ,\cdot ),R_{\cdot }(\cdot ,\cdot ))$で表される．ここで各要素はそれぞれ次を意味する．

• $S$ : 状態の有限集合
• $A$ : 行動 (action) の有限集合（状態 $s$ で取ることのできる行動の集合は $A_{s}\subset A$と書く）
• $P_{a}(s,s')=\Pr(s_{t+1}=s'\mid s_{t}=s,a_{t}=a)$ : 時刻 $t$ の行動を $a$ としたときの状態 $s$ から $s'$ への状態遷移確率
• $R_{a}(s,s')$ : 状態 s から s' に遷移する際に得られる即時報酬 (immediate reward) ，またはその期待値 (expected immediate reward)

※ 一般的なマルコフ決定過程の理論では $S$ および $A$ の有限性を仮定しないが、本記事での議論では基本的に有限性を仮定することに注意されたい．

問題設定

MDP における基本的な問題設定は，意思決定者の現在の状態が $s$ のときに取る行動を関数 $\pi (s)$ として表記する．

このようにマルコフ決定過程と政策を組み合わせると，各状態ごとに行動は固定され，結果として得られる組み合わせ(combination) はマルコフ連鎖として振る舞うことに注意されたい．

目標はランダムな報酬 (random reword) の累積関数（典型的には無限区間に渡る割引和の期待値）を最大化する政策 $\pi$ を選択することである．

$$\max _{\pi }\quad \mathbb {E} {\bigg [}\sum _{t=0}^{\infty }\gamma ^{t}R_{\pi (s_{t})}(s_{t},s_{t+1}){\bigg ]}$$

ここで $\gamma \in [0,1)$ は割引因子(discount factor) と呼ばれるは 値であり，現在の報酬と未来の報酬との間における重要度 (importance) の差を表す．

マルコフ性

マルコフ性により、この特定の問題における最適政策 (optimal policy) は状態 $s$ のみの関数として書くことができる．

アルゴリズム

MDPs は 線形計画法 または 動的計画法で解くことができる。ここでは後者によるアプローチを示す。

状態遷移関数 $P$ および 報酬関数 (reward function) $R$ は既知であると仮定し，割引された報酬の期待値を最大化する政策を求めることを考える．

最適政策 (optimal policy) を計算するためのこのような標準的なアルゴリズムの族 (standard family of algorithms) では，状態によって指標づけられた2つの値（価値 $V(s)$ ，政策 $\pi (s)$）の配列を格納するための記憶領域が必要となる．アルゴリズムが終了すると，$\pi (s)$ には解，$V(s)$ には解である行動に従うことで得られる報酬の割引和（の平均値）が格納される．

このアルゴリズムは、以下に示す二つのステップを持ち，すべての状態が変化しなくなるまで繰り返し計算する．各ステップにおける計算式は次のように定義される:

${\displaystyle }$

$$\pi (s):=\arg \max _{a}\left\{\sum _{s'}P_{a}(s,s'){\Big (}R_{a}(s,s')+\gamma V(s'){\Big )}\right\}$$

$$V(s):=\sum _{s'}P_{\pi (s)}(s,s'){\Big (}R_{\pi (s)}(s,s')+\gamma V(s'){\Big )}$$

これらの（計算量の）オーダーは使用するアルゴリズムの種類に依存する．状態がどの状態においても除外されることがない限り， アルゴリズムは最終的に正確な解に到達する．

価値反復法

価値反復法 (Bellman 1957)は，backward inductionとも呼ばれ，価値関数 $\pi (s)$ を直接使用する代わりに，必要な場合は $V(s)$ から計算する。 ロイド-Shapley による1953年の確率ゲーム#cite_note-FOOTNOTEShapley1953-2 に関する論文には MDP における価値反復法の特殊な場合が含まれるが，このことが認知されたのは後になってからである[3]

政策の計算式 $\pi (s)$ を価値関数 $V(s)$ の計算式に代入することで，次の結合されたステップが得られる:

$$V_{i+1}(s):=\max _{a}\left\{\sum _{s'}P_{a}(s,s'){\Big (}R_{a}(s,s')+\gamma V_{i}(s'){\Big )}\right\}$$

ここで $i$ は繰り返しのインデックスである。価値反復法は $i=0$ に $V_{0}$ を価値観数の推定値として開始する。 そしてすべての状態 $s$ に対し $V(s)$ の値が収束（左辺値と右辺値が一致）するまで繰り返し計算により $V_{i+1}$ を求める (これがこの問題における "ベルマン方程式"である)。

政策反復法

政策反復法 (Howard, 1960)では、一つ目のステップが1度評価され、二つのステップを収束するまで繰り返す。その後一つ目のステップを再度評価し，再び同じことを繰り返す。二つ目のステップは，収束するまで繰り返し計算する代わりにしばしば線形方程式として解を求める．

この手法は，明確な停止条件が存在することが利点に持つ．一つ目のステップをすべての状態に適用したとき $\pi$ の配列が変化しなければアルゴリズムは完了する．

修正政策反復法

修正政策反復法 (van Nunen 1976; Puterman & Shin 1978) では，一つ目のステップを評価し，その後二つ目のステップの計算を数回繰り返す．その後，一つ目のステップを再び一回評価する．

優先順序付け (Prioritized sweeping)

In this variant, the steps are preferentially applied to states which are in some way important - whether based on the algorithm (there were large changes in V or \pi around those states recently) or based on use (those states are near the starting state, or otherwise of interest to the person or program using the algorithm).  

拡張と一般化

部分観測マルコフ決定過程

上の解は，政策関数の値 $\pi (s)$ を計算する際に現在の状態 $s$ が既知であることを仮定している．状態観測に不確実性が伴う場合など，この仮定が成り立たない場合の一般化として，部分観測マルコフ決定過程 (Partially Observable Markov Decision Process; POMDP) が知られている．

この領域の主な進展は Burnetas と Katehakis の "Optimal adaptive policies for Markov decision processes" により得られた ．この文献では，有限ホライズンにわたる報酬和の期待値に対し (uniformly maximum convergence rate properties)を持つ適応的な政策のクラスが有限状態・有限入力の仮定かつ遷移測の規約性 (irreducibility) の元で構築された．These policies prescribe that the choice of actions, at each state and time period, should be based on indices that are inflations of the right-hand side of the estimated average reward optimality equations

強化学習

確率や報酬が未知の場合，問題は強化学習の一種となる (Sutton & Barto 1998).

この目的のためには，行動 a を取った後ずっと最適な行動（あるいは各時刻における可能な任意の行動）を継続した場合に対応する，より進んだ関数を定義するのが有効である．

$$Q(s,a)=\mathbb {E} _{\pi }{\bigg [}\sum _{k=0}^{\infty }\gamma ^{k}R_{a_{t+k}}(s_{t+k},s_{t+k+1}){\bigg |}s_{t}=s,a_{t}=a{\bigg ]}$$

この関数は行動価値関数と呼ばれる．

$$Q(s,a)=\sum _{s'}P_{a}(s,s'){\Big (}R_{a}(s,s')+\gamma V(s'){\Big )}$$

この関数もまた未知であるが，学習の間に用いられる経験 (experience) は（結果 s' を伴う）ペア (s, a) に基づく（すなわち，「私は状態 s にいて a を試行し， s' が起こった）．すなわち，意思決定者は Q の配列を持ち，その値を直接更新するために経験を用いる．これは Q 学習として知られている． 

強化学習は，遷移確率の仕様が明示的に与えれていないマルコフ決定過程を解くことができる（価値反復法／政策反復法では遷移確率の値が必要となる）．強化学習では，遷移確率の明示的な仕様の代わりに，遷移確率は一様乱数の初期状態から何度も試行されるシミュレータを介してアクセスされる．強化学習は膨大な数の状態への問題を扱うため関数近似と組み合わせることがある．

学習オートマトン

機械学習理論における MDP のもう一つの応用は学習オートマトン (Learning Automata) と呼ばれる．これは環境が確率的な挙動を示す場合における強化学習の一つでもある．学習オートマトンに関する最初の詳細な論文は 1974 年に Narendra と Thathachar により調査された（そこでは有限状態オートマトンと明示的に記載されている[5]）．強化学習と同様，学習オートマトンのアルゴリズムも確率や報酬が未知の場合の問題を解くことができる．Q学習の違いは，Q値を省略し，学習の結果を探すために行動の確率を直接求めることである．学習オートマトンは収束性が厳密に証明されている学習方法である[6]

学習オートマトンの理論では，次のように構成される 確率オートマトン (Stochastic Automaton) が用いられる:

• 可能な入力 (possible inputs) の集合 x,
• 可能な内部状態 (possible internal states) の集合 Φ = { Φ₁, ..., Φ_s } ,
• 可能な出力 (possible outputs) または行動の集合 α = { α₁, ..., α_r } , ただし r≤s,
• 初期状態確率ベクトル p(0) = ≪ p₁(0), ..., p_s(0) ≫,
• 各時刻 t における p(t), 現在の入力，および現在の状態 から p(t+1) を求める計算可能関数 (computable function) A,
• 各時刻における出力を与える関数 G: Φ → α
  

このようなオートマトンの状態は”dicrete-state discrete-parameter Markov process" の状態と対応する[7] ．各時刻 t=0,1,2,3,... においてオートマトンは環境から入力を読み込み，A により P(t) を P(t+1) に更新する．継続する状態は P(t+1) に基づき選択され，対応する行動が出力される．同様に，環境は（オートマトンの）行動を読み取り，次の入力をオートマトンに送信する[6]

Fuzzy Markov decision processes (FDMPs)

MDP では，最適政策は未来の報酬を最大化する政策である．したがって，最適政策は行動の有限集合に属するいくつかの行動で構成される．FDMP では，まず，価値観数を通常の（すなわち行動の有限集合の）MDPとして計算する．その後，政策はファジー推論システム (fuzzy inference system) により展開される．言い換えると，価値関数はファジー管理システムの入力として活用され，政策はファジー推論システムの出力である．

連続時間マルコフ決定過程

離散時間マルコフ決定過程では，意思決定は離散的な時間間隔で行われる．一方，連続時間マルコフ決定過程では，意思決定は意思決定者の選ぶ任意の時刻に行われる．離散時間マルコフ決定過程と比較し，連続時間マルコフ決定過程は連続的なダイナミクスを持つシステム，すなわちシステムのダイナミクスが変微分方程式で定義される場合の意思決定過程を議論するのにより適している．

定義

連続時間マルコフ決定過程を議論するため，次の2つの表記を導入する:

状態空間・行動空間 (action space) が有限の場合:

• ${\mathcal {S}}$: 状態空間
• ${\mathcal {A}}$: 行動空間
• $q(i|j,a)$: ${\mathcal {S}}\times {\mathcal {A}}\rightarrow \triangle {\mathcal {S}}$ : transition rate function
• $R(i,a)$: ${\mathcal {S}}\times {\mathcal {A}}\rightarrow \mathbb {R}$, 報酬関数

状態空間・行動空間 (action space) が連続の場合:

• ${\mathcal {X}}$: 状態空間
• ${\mathcal {U}}$: 可能な制御（入力）の空間
• $f(x,u)$: ${\mathcal {X}}\times {\mathcal {U}}\rightarrow \triangle {\mathcal {X}}$ : transition rate function
• $r(x,u)$: ${\mathcal {X}}\times {\mathcal {U}}\rightarrow \mathbb {R}$ : reward rate function．$R(x,u)$ を前節で議論した報酬関数としたとき $r(x(t),u(t))dt=dR(x(t),u(t))$ を満たす

問題設定

離散時間マルコフ決定過程と同様，連続時間マルコフ決定過程では次式で与えられる最適期待積分利得 (optimal expected integrated reward) を与える最適政策 (optimal policy) または最適制御 (optimal control) を求めることが目的となる．

$$\max _{u}\ \mathbb {E} \left[\int _{0}^{\infty }\gamma ^{t}r(x(t),u(t)))\,dt\ {\bigg |}\ x_{0}\right]$$

ただし，$0\leq \gamma <1$ である．

線形計画法による定式化

状態と行動が有限の場合，最適政策を求めるのに線形計画法を用いることが出来る（これは初期のアプローチを応用したものである）．ここではエルゴード性を満たすモデル (ergodic model) のみを考える．これは連続時間の MDP が定常な政策の下でエルゴード性を満たす連続時間マルコフ連鎖となることを意味する．この仮定の下では，現在の状態からどの時刻における意思決定を行えるにもかかわらず，意思決定者は1つより多くの行動をとることでより多くの利益を得ることが出来ない．彼にとっては，システムが現在の状態からほかの状態に遷移する場合の行動をとるのがより望ましい．

いくつかの条件のもと（詳細は Continuous-Time Markov Decision Processes の補題3.14を確認されたい），最適な価値関数 $V^{*}$ が状態 $i$ と独立な場合，次の不等式を得る:

$$g\geq R(i,a)+\sum _{j\in S}q(j\mid i,a)h(j)\quad \forall i\in S\ {\text{and}}\ \forall a\in A(i)$$

もし関数 h が存在すれば， ${\bar {V}}^{*}$ は上式を満たす $g$ の最小値となる．${\bar {V}}^{*}$ を求めるため，次に示す線形計画モデルを用いることができる:

• 主問題 (P-LP)
  $${\begin{aligned}{\text{Minimize}}\quad &g\\{\text{s.t}}\quad &g-\sum _{j\in S}q(j|i,a)h(j)\geq R(i,a)\,\,\forall i\in S,\,a\in A(i)\end{aligned}}$$
• 双対問題 (D-LP)
  $${\begin{aligned}{\text{Maximize}}\quad &\sum _{i\in S}\sum _{a\in A(i)}R(i,a)y(i,a)\\{\text{s.t}}\quad &\sum _{i\in S}\sum _{a\in A(i)}q(j\mid i,a)y(i,a)=0\quad \forall j\in S,\\&\sum _{i\in S}\sum _{a\in A(i)}y(i,a)=1,\\&y(i,a)\geq 0\qquad \forall a\in A(i){\text{ and }}\forall i\in S\end{aligned}}$$

ハミルトン・ヤコビ・ベルマン方程式

連続時間の MDP において状態と行動が連続な場合，最適基準 (optimal critarion) は ハミルトン・ヤコビ・ベルマン方程式を解くことによって得られる．いま，HBJ方程式の議論のため問題を次のように書き換える:

$${\begin{aligned}V(x(0),0)=&\max _{u}\int _{0}^{T}r(x(t),u(t))dt+D[x(T)]\\s.t.\quad &{\frac {dx(t)}{dt}}=f[t,x(t),u(t)]\end{aligned}}$$

ここで，$D(\cdot )$ は終端報酬関数 (terminal reward function)， $x(t)$ はシステムの状態ベクトル，$u(t)$ はシステムの制御入力である． $f(\cdot ,\cdot ,\cdot )$ は状態ベクトルの時間発展を表す．上の問題に関するハミルトン・ヤコビ・ベルマン方程式は次のように表される:

$$\max _{u}\left\{r(t,x,u)+{\frac {\partial V(t,x)}{\partial x}}f(t,x,u)\right\}=0$$

この方程式を解くことで，価値関数の最大値 $V^{*}$ を与える最適制御 (optimal control) $u^{*}(t)$ を求めることが出来る．

応用

連続時間マルコフ決定過程は，待ち行列システム (Queueing System)，epidemic process, 個体群過程 (population process) などに応用がされている．

制約付きマルコフ決定過程

制約付きマルコフ決定過程 (Constrained Markov Decision Processes; CMDPs) はマルコフ決定過程の拡張である．MDPs と CMDPs には3つの基本的な違いがある:[9]

• ある行動をほかのものの代わりに適用した後で（複数の）コストが発生する
• CMDP は線形計画法のみで解くことが出来る（動的計画法を用いることはできない）
• 終端時刻における政策が初期状態に依存する

CMDP の応用例は数多く存在し，最近ではロボット工学におけるモーションプランニングに用いられている[10]

参照

• 確率論的オートマトン
• 量子有限オートマトン
• 部分観測決定過程
• 動的計画法
• Bellman方程式 の経済学への応用
• Hamilton–Jacobi–Bellman 方程式
• 最適制御
• 再帰的経済学
• Mabinogion羊の問題
• 確率ゲーム
• Q-learning

References

• Bellman, R. (1957). “A Markovian Decision Process”. Journal of Mathematics and Mechanics 6. http://www.iumj.indiana.edu/IUMJ/FULLTEXT/1957/6/56038. 
• Bellman., R. E. (2003). Dynamic Programming (Dover paperback edition ed.). Princeton, NJ: Princeton University Press. ISBN 0-486-42809-5 
• Howard, Ronald A. (1960). Dynamic Programming and Markov Processes. The M.I.T. Press. http://web.mit.edu/dimitrib/www/dpchapter.pdf 
• Shapley, Lloyd (1953). “Stochastic Games”. Proceedings of National Academy of Science 39: 1095–1100. 
• Kallenberg, Lodewijk (2002). “Finite state and action MDPs”. Handbook of Markov decision processes: methods and applications. Springer. ISBN 0-7923-7459-2 
• Bertsekas, D. (1995). Dynamic Programming and Optimal Control. 2. MA: Athena 
• Burnetas, A.N.; Katehakis, M. N. (1997). “Optimal Adaptive Policies for Markov Decision Processes”. Mathematics of Operations Research 22 (1): 222. doi:10.1287/moor.22.1.222. 
• Feinberg, E.A.; Shwartz, A., eds (2002). Handbook of Markov Decision Processes. Boston, MA: Kluwer 
• Derman, C. (1970). Finite state Markovian decision processes. Academic Press 
• Puterman., M. L. (1994). Markov Decision Processes. Wiley 
• Tijms., H.C. (2003). A First Course in Stochastic Models. Wiley 
• Sutton, R. S.; Barto, A. G. (1998). Reinforcement Learning: An Introduction. Cambridge, MA: The MIT Press. http://webdocs.cs.ualberta.ca/~sutton/book/the-book.html 
• van Nunen, J.A. E. E (1976). “A set of successive approximation methods for discounted Markovian decision problems. Z”. Operations Research 20: 203-208. 
• Narendra, K. S.; Thathachar, M. A. L. (1974-07-01). “Learning Automata - A Survey”. IEEE Transactions on Systems, Man, and Cybernetics SMC-4 (4): 323–334. doi:10.1109/TSMC.1974.5408453. ISSN 0018-9472. http://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=5408453. 
• Narendra, Kumpati S.; Thathachar, Mandayam A. L. (1989) (英語). Learning automata: An introduction. Prentice Hall. ISBN 9780134855585. https://books.google.com/books?id=hHVQAAAAMAAJ 
• Meyn, S. P. (2007). Control Techniques for Complex Networks. Cambridge University Press. ISBN 978-0-521-88441-9. オリジナルの19 Jun 2010時点におけるアーカイブ。. https://web.archive.org/web/20100619011046/https://netfiles.uiuc.edu/meyn/www/spm_files/CTCN/CTCN.html  Appendix contains abridged “Meyn & Tweedie”. 2012年12月18日時点のオリジナルよりアーカイブ。
• Ross, S. M. (1983). Introduction to stochastic dynamic programming. Academic press 
• Guo, X.; Hernández-Lerma, O. (2009). Continuous-Time Markov Decision Processes. Springer. http://www.springer.com/mathematics/applications/book/978-3-642-02546-4 
• Puterman, M. L.; Shin, M. C. (1978). “Modified Policy Iteration Algorithms for Discounted Markov Decision Problems”. Management Science 24. 
• Altman, Eitan (1999). Constrained Markov decision processes. 7. CRC Press 
• Feyzabadi, S.; Carpin, S. (18–22 August 2014). "Risk-aware path planning using hierarchical constrained Markov Decision Processes". Automation Science and Engineering (CASE). IEEE International Conference. pp. 297, 303. {{cite conference}}: 引数|ref=harvは不正です。 (説明)

External links

• MDP Toolbox for MATLAB, GNU Octave, Scilab and R The Markov Decision Processes (MDP) Toolbox.
• MDP Toolbox for Matlab - An excellent tutorial and Matlab toolbox for working with MDPs.
• MDP Toolbox for Python A package for solving MDPs
• Reinforcement Learning An Introduction by Richard S. Sutton and Andrew G. Barto
• SPUDD A structured MDP solver for download by Jesse Hoey
• Learning to Solve Markovian Decision Processes by Satinder P. Singh
• Optimal Adaptive Policies for Markov Decision Processes by Burnetas and Katehakis (1997).