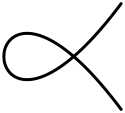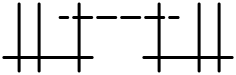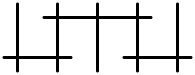「楕円曲面」の版間の差分
Enyokoyama (会話 | 投稿記録) |
(相違点なし)
|
2014年7月17日 (木) 03:18時点における版
数学では、楕円曲面(elliptic surface)は楕円ファイバーを持つ曲面であり、言い換えると、曲面からの代数曲線への連結な固有(proper)射が、ほとんどの点上のファイバーを楕円曲線とするような曲面である。
ファイバーが楕円曲線とならない点を特異点ファイバー(singular fibers)と呼び、小平邦彦(Kunihiko Kodaira)により分類された。弦理論の脈絡では、楕円ファイバーも特異ファイバーもF-理論(F-theory)を使う記述にとっても重要である。
楕円曲面は、曲面の興味深い例の多くを含む、曲面の大きなクラスで、複素幾何学の観点からも滑らかな(smooth)4-次元多様体(4-manifold)の理論の観点からも、比較的良く理解されている。楕円曲面は代数体上の楕円曲線に似ている（つまり、類似している）。
例
- 任意の曲線の任意の楕円曲線の積（この場合、特異ファイバーはない）
- 小平次元 1 の全ての曲面は楕円曲面
- 全てのエンリケス曲面は楕円的で、射影直線上に楕円ファイバーを持っている
- 小平曲面
- ドルガチョフ曲面(Dolgachev surface)
- 塩田モジュラ曲面(Shioda modular surface)
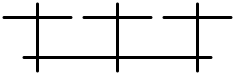
特異ファイバーの小平による表
楕円ファイバーのファイバーの大半は、（非特異）楕円曲線である。残ったファイバーを特異ファイバーと言う。特異ファイバーは有限個しかなく、特異点を持つかもしれなく又は 0 でない多重度ももつかもしれない有理曲線の合併により構成される。小平とネロンは独立に可能なファイバーを分類し、テイトのアルゴリズム(Tate's algorithm)は、数体の楕円曲線の上のファイバーのタイプを探すことに使うことができる。
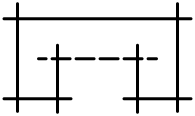
次の表は、極小な楕円ファイバー構造の可能な限りのファイバーを一覧化した。（「極小」は、大まかには、それよりも「小さな」ファイバーには分解することができないファイバーを言う。曲面の場合には、特異ファイバーは極小な曲線は含まないことを意味する。）
エンリケス・小平の分類
- ファイバーの小平の記法
- ファイバーのアンドレ・ネロン(André Néron)の記号
- （タイプ I0 以外の全ての有理）ファイバーの既約成分の数
- 成分の交叉行列、これは 1×1 の零行列(zero matrix)かまたは、アフィンカルタン行列(affine Cartan matrix)で、そのディンキン図形(Dynkin diagram)は与えられている。
- 各々のファイバーの多重度はディンキン図形により表される。
| 小平 | ネロン | 成分 | 交叉行列 | ディンキン図形 | ファイバー |
|---|---|---|---|---|---|
| I0 | A | 1 (楕円的) | 0 |  |
|
| I1 | B1 | 1 (二重点を持つ) | 0 | |
|
| I2 | B2 | 2 (2 つの異なる交点を持つ) | アフィン A1 |  |
|
| Iv (v≥2) | Bv | v (v 個の異なる交点を持つ) | アフィン Av-1 |  |
|
| mIv (v≥0, m≥2) | Iv 多重度 m | ||||
| II | C1 | 1 (カスプを持つ) | 0 | |
|
| III | C2 | 2 (位数 2 の一つの点で交叉) | affine A1 | |
|
| IV | C3 | 3 (全て一つの点で交叉) | アフィン A2 |  |
|
| I0* | C4 | 5 | アフィン D4 |  |
|
| Iv* (v≥1) | C5,v | 5+v | アフィン D4+v |  |
|
| IV* | C6 | 7 | アフィン E6 |  |
|
| III* | C7 | 8 | アフィン E7 |  |
|
| II* | C8 | 9 | アフィン E8 |  |
|
この表は、次のようにして見つけ出すことができる。幾何学的議論により、ファイバーの構成要素の交叉行列は、負の半定置で、連結対称で、（最小性により）− 1 に等しい対角要素を持たない行列である必要がある。そのような行列は 0 かまたは、タイプADE(ADE)のアフィンディンキン図形のカルタン行列の積である必要がある。
交叉行列は 3つの例外をとしてファイバーのタイプを決定する。
- 交叉行列が 0 であれば、ファイバーは楕円曲線 (タイプ I0) であるか、または、タイプ I1 かタイプ II のカスプの二重点を持っている場合
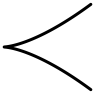
- 交叉行列がアフィン A1 であれば、交叉多重度が 2 である 2つの成分が存在する場合。それらは位数 1 (タイプ I2) か、または、位数 2 (タイプ III) の 2つの交点を持つことができる。
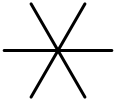
- 交叉行列がアフィン A2 のとき、3つの成分が交叉する場合。 交点は 3つの異なる点のペア (タイプ I3) であるか、または、同一の点 (タイプ IV) であるかのどちらかである。
対数変換
楕円曲面、もしくは楕円ファイバーの（位数 m 中心 p の）対数変換(logarithmic transformation)は、ベース空間の点 p での多重度 1 のファイバーを多重度 m のファイバーへ変換する。逆も可能なので、高い多重度のファイバーは多重度 1 へ全て変換することができ、全ての多重なファイバーを省くことができる。
対数変換は非常に荒々しく使うことができ、小平次元を変えたり、代数曲面を非代数曲面へ変換することもできる。
例: L を C の格子 Z+iZ とし、E を楕円曲線 C/L とすると、E×C から C への射影写像は、楕円ファイバーである。0 上のファイバーを多重度 2 のファイバーへどのように置き換えるかを示す。
(c,s) を (c+1/2, −s) へ写す位数 2 の E×C 上の自己同型が存在する。この群作用による E×C の商空間を X とする。(c,s) から s2 と写すことで X を C 上のファイバー空間とする。X から 0 上のファイバーを引いた空間から E×C から 0 上のファイバーを引いた空間へのファイバー構造を、(c,s) から (c-log(s)/2πi,s2) により定義する。（0 上の 2つのファイバーは楕円曲線には同型ではないので、ファイバー空間 X は確かに C 上の全てでファイバー空間 E×C と同型ではない。
ファイバー空間 X は 0 上で多重度 2 のファイバーを持っていて、そうでないところでは E×C のように見える。このことを、X は 0 を中心とした E×C への位数 2 の対数変換を適用することによって得ることができるという。
参照項目
- エンリケス・小平の分類
- ネロン極小モデル(Néron minimal model)
参考文献
- Barth, Wolf P.; Hulek, Klaus; Peters, Chris A.M.; Van de Ven, Antonius. Compact Complex Surfaces. Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. 4 (2nd enlarged ed.). Berlin: Springer-Verlag. ISBN 3-540-00832-2. Zbl 1036.14016.
- Kodaira, Kunihiko (1964). “On the structure of compact complex analytic surfaces. I”. Am. J. Math. 86: 751–798. doi:10.2307/2373157. Zbl 0137.17501.
- Kodaira, Kunihiko (1966). “On the structure of compact complex analytic surfaces. II”. Am. J. Math. 88: 682–721. doi:10.2307/2373150. Zbl 0193.37701.
- Néron, André (1964). “Modeles minimaux des variétés abeliennes sur les corps locaux et globaux” (French). Publications Mathématiques de l'IHÉS 21: 5–128. doi:10.1007/BF02684271. MR0179172. Zbl 0132.41403.