二分ヒープ

二分ヒープ(にぶんヒープ,バイナリヒープ,Binary heap)とは、二分木を使って作られるヒープ(データ構造)の特に単純な種類のひとつである。それは、二分木に2つの制約を追加したものとみなせる。
- 形特性
- 木は完全にバランスの取れた二分木(すべての葉は同じ高さにある)になるか、木のもっとも高い方がすべて埋まっていないならば、ノードは左から右へ順に埋まっていく。
- ヒーププロパティ
- データ構造全体を決定するための比較述語にしたがって、各々のノードはそのノードの子よりも大きいか等しくなるように配置される。
「より大きい」とは、ヒープをソートするためにどの比較関数を選択するかによって意味づけられ、ノード内のデータが常に数値であるとは限らないので数学的感覚での『より大きい』必要はない。比較関数が数学的な「より大きい」であるヒープは最大ヒープ (max heap) と呼ばれる。また、比較関数が数学的な「より小さい」であるヒープは最小ヒープ (min heap) と呼ばれる。通常は、優先順位付き待ち行列にすぐに適用できることから、最小ヒープが使われる。
ヒープ内の子同士の順序は、ヒーププロパティによって特定できないことに注意すること。つまり、親を同じくする二つの子は、Treapと比較して形特性を壊さない限り自由に入れ替えることができる。
ヒープ操作
ヒープへの追加
すでに存在しているヒープに要素を追加するには、ヒーププロパティを保つために、「up-heap」、「bubble-up」、「percolate-up」、「sift-up」として知られている操作を用いることができる。以下のアルゴリズムにしたがって、二分ヒープを用いてO(log n)で操作を行うことができる。
- ヒープの最下層に要素を追加する
- 追加した要素とその親を比較する。正しい順序で並んでいるならば、停止する。
- もし順序が正しくないならば、親と追加要素を交換して、2に戻る。
我々は、この操作をツリー上で最大各々の深さで行う必要がある。つまり、木の高さ分行う必要があるので、O(log n)かかる。しかしながら、およそ要素の50%が葉であり最下層から2レベルまでには75%の要素が含まれることから、新しい要素を挿入する際、ヒープを維持するために、上向きに2, 3レベル動かすくらいですむだろう。このように、二分ヒープは、要素の挿入には平均O(1)の固定時間をサポートする。
我々が最大ヒープと読んでいるものは以下のようなものである。
11
/ \
5 8
/ \ /
3 4 X
ここで、ヒープに「15」という数字を付け加えたい。まず最初にXの印がついている場所に「15」を置く。しかし、「15」は親である「8」より大きいのでヒーププロパティに違反している。そこで、「15」と「8」を入れ替える。最初の入れ替え後、ヒープは以下の様に見える。
11
/ \
5 15
/ \ /
3 4 8
しかし「15」はその親である「11」よりも大きいので、まだヒーププロパティに違反している。そこで、再度入れ替える必要がある。
15
/ \
5 11
/ \ /
3 4 8
これで、適切な最大ヒープができた。
ヒープからルートの削除
ヒープからルートを削除する手順、つまり効果的に最大ヒープ内で最大要素を検索したり最小ヒープから最小要素を検索する手順は、up-heapとよく似ている。ルートを削除するということは、ルートを木の末端の要素と入れ替えることである。前と同じ最大ヒープを例にとると、
11
/ \
5 8
/ \
3 4
「11」を削除して「4」と入れ替える。
4
/ \
5 8
/
3
親である「4」は子である「8」よりも小さいのでヒーププロパティに違反している。この2つの要素を交換すればヒーププロパティは保たれ(「4」はより大きい子と交換される。最小ヒープならばより小さい子と交換される)、これ以上操作の必要はない。
8
/ \
5 4
/
3
ヒープの実装
古典的な二分木データ構造を使って二分ヒープを実装するのは完全に可能である。ただ、アルゴリズム的に要素を追加したりノードに余分なデータを追加するときに、二分ヒープ上の末端の隣接する要素を探す問題がある。これは「スレッド木」と呼ばれている。これは単に子への参照を持っておく代わりに、ノードの後続節点順に格納する方法である。
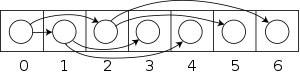
しかし、より普及しているやり方は、配列にヒープを格納する方法である。どんな二分木でもひとつの配列に格納できる。ヒープはいつもほとんど完全な二分木であるので、コンパクトに格納できる。ポインタ用のスペースは必要ない。代わりに、インデックスiそれぞれについて、要素a[i]は2つの子a[2i+1]とa[2i+2]の親である。以上を図に示す。(ルートは0から始まるように実装し、a[i]の親はa[floor((i-1)/2)]になる。これは暗黙のデータ構造の一つの単純な例である。)
このやり方は、ヒープソートアルゴリズムで特に役に立つ。入力配列内の領域をヒープを格納するために再利用できるからである。
upheap/downheap操作は次のような配列の点から説明できる。ヒーププロパティはb, b+1, …, eとインデックスされていると仮定する。配列をずらす関数はヒーププロパティをb-1, b, b+1, …, eと拡張する。そのうち、index i = b-1 のみヒーププロパティを違反することができる。ここで、b, …, eまでの範囲内でa[i]のもっとも大きな値の子のインデックスをjとする。(もし、このようなインデックスが存在しないならば、2i > eということはヒーププロパティは新たに拡張された範囲を保持し、それ以上することは何も無いからである。)a[i]とa[j]の値を交換することにより、iの位置のヒーププロパティは成立される。唯一の問題はヒーププロパティはインデックスjを保持しないかもしれないことである。配列をずらす関数はヒーププロパティがすべての要素において成立するまで、後ろから再帰的にindex jまで適用する。
配列をずらす関数は高速である。それぞれの処理単位では、2つの比較と1つの交換のみが必要である。ループ1回につきインデックス値は2倍になるので、最大log2e回処理が行われる。
二分ヒープ内でのマージ操作は、等しいサイズのヒープサイズだとΘ(n)だけかかる。マージ処理がよく使われる処理であるならば、二項ヒープのような違うヒープ実装を推奨する。
