AVL木

AVL木(えーぶいえるき、AVL tree、Adelson-Velskii and Landis' tree)とは、コンピュータサイエンスにおいて、「どのノードの左右部分木の高さの差も1以下」という条件を満たす二分探索木のことである。
平衡二分探索木の1つで、木に対する操作によって条件を満たさないノードが発生しても、回転と呼ばれる操作を行うだけで木をAVL木に再構成でき、平衡を維持できる。
AVL木は最初に考案された平衡二分探索木であり、その名は1962年に論文を発表したソ連の2人の数学者、ゲオルギー・アデルソン・ヴェルスキーとエフゲニー・ランディスに由来する。
平衡条件と計算量[編集]
通常の二分探索木は入力されるデータの順番によって木の構成が変わるため、探索効率が安定しない。例えば、データがソートされた状態で順に入力されると、木は線形リストと等価な構造になるため、探索の計算量は最悪のになってしまう。木が完全二分木であれば計算量は最良のになるが、完全二分木でなくとも木全体の高さがより小さくバランスが取れている状態、すなわち平衡な状態であれば木の性能は十分発揮できる。AVL木は「どのノードの左右部分木の高さの差も1以下」であることを平衡の条件としており、これを常に満たすので、探索の計算量は常に程度になる。
平衡係数[編集]
AVL木では、1つのデータを挿入、削除する度に全てのノードが条件を満たしているか調べる。ここでは、その手がかりとして各ノードに平衡係数を持たせることを考える。平衡係数は以下のように各ノードの左右部分木の高さの差で定義する(左右は逆でもよい)。
(平衡係数) = (左部分木の高さ) - (右部分木の高さ)
平衡係数は挿入や削除などの操作の度に再計算する。すなわち、左部分木の方が高くなるほど+1、右部分木の方が高くなるほど-1すればよい。
平衡係数が2以上または-2以下のノードが存在する時、木の再構成が必要である。再構成後は平衡係数を更新する。
操作[編集]
AVL木の基本操作は通常の二分探索木に対して行うものと同じだが、木の平衡が崩れた時は木を再構成するために回転も行う。回転は、平衡係数が2以上または-2以下のノードのうち最も根から遠いノード、すなわち最も葉に近いノードから行う。
回転操作の詳細は「木の回転」を参照のこと。
探索[編集]
木の中から目的の値を持つノードを見つけ出すのが探索である。AVL木の探索は通常の二分探索木と同様の手順で、「左の子の値 ≤ 親の値 ≤ 右の子の値」の条件を手がかりに行う。
- 根ノードに着目する
- 着目しているノードが存在しなければ、木に目的の値を持つノードはないので処理を終了(※)
- 「着目しているノードの値」と「目的の値」を比較する
- 値が等しければ探索終了
- 「目的の値 < 着目しているノードの値」であれば、左の子ノードを新たに着目するノードとして(※)から繰り返す
- 「着目しているノードの値 < 目的の値」であれば、右の子ノードを新たに着目するノードとして(※)から繰り返す
挿入[編集]

通常の二分探索木における挿入は、条件「左の子の値 ≤ 親の値 ≤ 右の子の値」を満たす枝の末端を探索し、そこに新たに作成したノードを繋ぐだけであるが、AVL木ではさらに平衡条件を満たしているか調べ、満たしていない場合は回転を行う。
まず、挿入すべき枝の末端を探索しながら、探索してきた経路を記憶しておく。これはスタックや再帰呼出しを用いることで実現できる。挿入後、この経路上を「挿入したノードの親ノード」から「根ノード」に向かって順に調べていく。
平衡条件を満たさないノード(Pとする)があった場合に回転を行うが、ほとんどの場合、「P」と「Pの高い方の部分木の根ノード」に着目して1度回転を行えば、これらのノードとその子孫ノードは平衡条件を満たした状態になる。この回転を単回転または1重回転などと呼ぶ。
ただし、単回転では平衡条件が満たされない場合があることに注意しなければならない。具体的には、
- Pの左部分木の方が高く、かつPの左の子ノードの右部分木の方が高い場合(図のLeft Right Case)
- Pの右部分木の方が高く、かつPの右の子ノードの左部分木の方が高い場合(図のRight Left Case)
の2通りである。
この場合はそれぞれ以下のように2度回転を行うことで解決できる。これを複回転または2重回転などと呼ぶ。
- 回転前のPの左の子ノードをL、Lの右の子ノードをLRとすると、まずLとLRで回転し、次にPと新たにPの左の子ノードとなったLRで回転する
- 回転前のPの右の子ノードをR、Rの左の子ノードをRLとすると、まずRとRLで回転し、次にPと新たにPの右の子ノードとなったRLで回転する
このように、AVL木では部分木の構造によって単回転と複回転を使い分ける必要がある。
挿入後の平衡確認の終了条件[編集]
AVL木の挿入における平衡条件の確認は、探索してきた経路上の全てのノードが平衡条件を満たしていることを確認する必要は必ずしもなく、探索してきた経路上のどこかのノードを回転するか、探索してきた経路上に平衡係数が0のノードを見つけた時点で処理を終了できる。
なぜなら、挿入は木の高さを1大きくする操作であるのに対して、回転は木の高さを1小さくする操作であるから、これらの操作によってその部分木の高さが挿入前と等しくなるためである。また、挿入により平衡係数が0になったノードがあるということは、挿入前に高さが1小さかった方の部分木に挿入したということであるから、そのノードを根とする部分木の高さは挿入前後で変わっていないので、全てのノードが平衡条件を満たしていることがわかる。
ただし、探索してきた経路上に平衡係数が1もしくは-1のノードを見つけても処理を終了できない。
なぜなら、挿入により平衡係数が1もしくは-1になったノードがあるということは、挿入前のそのノードの左右部分木の高さは等しかったが、挿入により一方の部分木の高さが1大きくなったということであり、そのノードを根とする部分木の高さは1大きくなっているので、全てのノードが平衡条件を満たしていることを保証できないからである。
削除[編集]
AVL木の削除は、通常の二分探索木と同様の削除操作を行ったあと、平衡条件を満たしているか調べ、満たしていない場合は回転を行う。
挿入と同様に、まずは探索してきた経路上を「削除したノードの親ノード」から「根ノード」に向かって順に調べていく。平衡条件を満たさないノードがあった場合、そのノードと高い方の部分木の根ノードに着目して単回転、または複回転を行う。
なお、削除するノードが子ノードを2つ持つ場合、削除するノードの左部分木のうち最大値を持つノード(もしくは右部分木のうち最小値を持つノード)を探索して、削除するノードと置き換える処理が発生するが、ここで探索した経路も記憶しておく必要があることに注意する。ノードを削除するのは置き換え後なので、平衡条件の確認も置き換えられた先の親ノードから始めなければならない。
削除後の平衡確認の終了条件[編集]
AVL木の削除における平衡条件の確認は、探索してきた経路上の全てのノードが平衡条件を満たしていることを確認する必要は必ずしもなく、探索してきた経路上に平衡係数が1もしくは-1のノードを見つけた時点で処理を終了できる。
なぜなら、削除により平衡係数が1もしくは-1になったノードがあるということは、削除前のそのノードの左右部分木の高さは等しかったが、削除により一方の部分木の高さが1小さくなったということであり、そのノードを根とする部分木の高さは削除前後で変わっていないので、全てのノードが平衡条件を満たしていることがわかるからである。
ただし、探索してきた経路上のどこかのノードを回転したり、平衡係数が0のノードを見つけても処理を終了できない。
なぜなら、削除は木の高さを1小さくする操作であるのに対して、回転も木の高さを1小さくする操作であるから、これらの操作によって平衡条件を満たさなくなったノードが出てくる可能性があるためである。また、削除により平衡係数が0になったノードがあるということは、削除前に高さが1大きかった方の部分木から削除したということであるから、そのノードを根とする部分木の高さは1小さくなるので、同様の可能性がある。
特徴[編集]
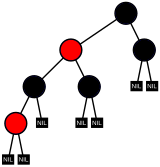
子ノードがない場合は部分木の高さを0と考えるため、1つの子ノードしか持たないノードについて、その子ノードは葉ノードとなる。すなわち、兄弟ノードを持たないノードは必ず葉ノードである。
AVL木のどの部分木もAVL木である。
AVL木は、あくまで各ノードの左右部分木の高さのバランスを保った木であり、各葉ノードの深さが均等な木というわけではない。深さが最も大きい葉ノードと最も小さい葉ノードの深さの差が2以上になって、完全二分木とはかけ離れた構造になることもある。
挿入や削除の操作は、毎回平衡条件の判定を伴うため比較的コストが掛かる。そのため、これらの操作が探索に比べてあまりにも頻繁に行われるような環境では、AVL木は性能を発揮しにくい。
AVL木は、同じく平衡二分探索木の1つである赤黒木に比べて平衡性をより厳密に維持するので、探索性能はAVL木の方がよいが、挿入や削除の性能は赤黒木の方がよい。


