田辺・菅野ダイアグラム
田辺・菅野ダイアグラム(たなべ・すがのダイアグラム、Tanabe–Sugano diagram)は、第4周期dブロック元素の正八面体型錯体における結晶場あるいは配位子場の強さと各スペクトル項のエネルギーの相関を表したグラフのことである。
概要[編集]
田辺・菅野ダイアグラムは横軸に配位子場の強さDq(配位子場分裂の大きさ)(またはΔo)をラカーパラメータBで割った値、縦軸に各スペクトル項の基底状態とのエネルギー差EをBで割った値をとり、各スペクトル項についてプロットしたものである。ただしD とq は
R は中心イオンから点電荷までの距離、Z は陰イオンの価数、e は電荷、R3d は3d電子の動径波動関数である。 各スペクトル項の基底状態とのエネルギー差Eは、配位子場の強さΔo、中心金属のラカーパラメータB、Cを使って表すことができる。配位子場の強さに応じてCとBの比が変化しないとすると、エネルギーはΔoとBのみで表すことができる。 実際C/Bはほぼ一定の値を持つ。EおよびΔoをBを単位として表すと、Bの値によらずに1つのグラフで表せる。またDqの大きいところで摂動論で配置間相互作用を取り入れた結果は点線で表されている。これが田辺・菅野ダイアグラムである。
田辺・菅野ダイアグラムの左端(配位子場が0)は自由な金属イオンに対応し、ここには原子のスペクトル項が示されている。そこから配位子場によって縮退が解けて、各スペクトル項に分裂する様子が示されている。エネルギーの0点は基底状態であるが、d電子がd4~d7の錯体については配位子場が弱いときには高スピン錯体、配位子場が強いときには低スピン錯体となるため、基底状態のスペクトル項が配位子場によって変化する。そのため、エネルギーのプロットも境界となる配位子場の値で折れ曲がる。エネルギーのプロットにはほぼ直線のものと緩やかな曲線になるものの2種類がある。前者は他に同じ対称性のスペクトル項が存在しない状態に、後者は他に同じ対称性のスペクトル項が存在する状態に対応する。同じ対称性のスペクトル項のエネルギーのプロットには非交差則が成り立つためにこのような形になる。
応用[編集]
田辺・菅野ダイアグラムを用いると、紫外可視吸収スペクトルの吸収極大波長(スペクトル項間のエネルギー差に対応する)から配位子場の強さを求めることができる。また、吸収が観測できないスペクトル項のエネルギーがどの程度かを予測することもできる。
背景[編集]
田辺行人と菅野暁が論文「On the absorption spectra of complex ions」を投稿するまで,錯体金属イオンの励起電子状態についての詳細はほとんど知られていなかった. 彼らはハンス・ベーテの結晶場理論とジュリオ・ラカーのスレーター積分の線形結合(現在ではラカーパラメーターと呼ばれている)を用いて, [1] 八面体錯体イオンの吸収スペクトルについて定量的に説明しようとした. [2] 彼らは多くの実験によって,等電子的な第一周期の遷移金属における傾向に基づいて,各d電子配置における配置間相互作用の行列式と、ラカーパラメータB,Cの値を見積もった. それぞれの電子配置の状態で計算されたエネルギーのプロットは「田辺・菅野ダイヤグラム」として知られている.[3][4]
分裂[編集]
| 項記号 | 縮退度 | 正八面体場での状態(マリケン記号) |
|---|---|---|
| S | 1 | A1g |
| P | 3 | T1g |
| D | 5 | Eg + T2g |
| F | 7 | A2g + T1g + T2g |
| G | 9 | A1g + Eg + T1g + T2g |
| H | 11 | Eg + T1g + T1g + T2g |
| I | 13 | A1g + A2g + Eg + T1g + T2g + T2g |
田辺・菅野ダイアグラム[編集]
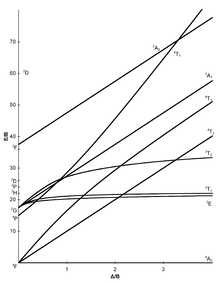
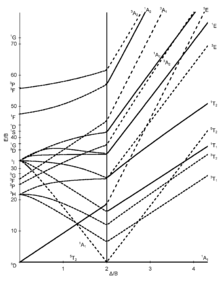
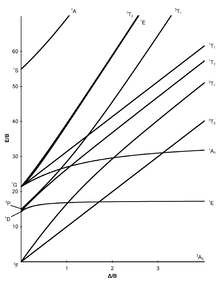
八面体錯体における7つの田辺・菅野ダイアグラムを以下に示す。[5] [6][7]
 |
 |
 |
 |
 |
 |
 |
参考文献[編集]
- ^ Racah, Giulio (1942). “Theory of complex spectra II”. Physical Review 62: 438–462. Bibcode: 1942PhRv...62..438R. doi:10.1103/PhysRev.62.438.
- ^ Tanabe, Yukito; Sugano, Satoru (1954). “On the absorption spectra of complex ions I”. Journal of the Physical Society of Japan 9 (5): 753–766. doi:10.1143/JPSJ.9.753.
- ^ Tanabe, Yukito; Sugano, Satoru (1954). “On the absorption spectra of complex ions II”. Journal of the Physical Society of Japan 9 (5): 766–779. doi:10.1143/JPSJ.9.766.
- ^ Tanabe, Yukito; Sugano, Satoru (1956). “On the absorption spectra of complex ions III”. Journal of the Physical Society of Japan 11 (8): 864–877. doi:10.1143/JPSJ.11.864.
- ^ Atkins, Peter; Overton, Tina; Rourke, Jonathan; Weller, Mark; Armstrong, Fraser; Salvador, Paul; Hagerman, Michael; Spiro, Thomas et al. (2006). Shriver & Atkins Inorganic Chemistry (4th ed.). New York: W.H. Freeman and Company. pp. 478–483. ISBN 0-7167-4878-9
- ^ Lancashire, Robert John (4–10 June 1999), “Interpretation of the spectra of first-row transition metal complexes”, CONFCHEM, ACS Division of Chemical Education
- ^ Lancashire, Robert John (2006年9月25日). “Tanabe-Sugano diagrams via spreadsheets”. 2009年11月29日閲覧。


