動径分布関数
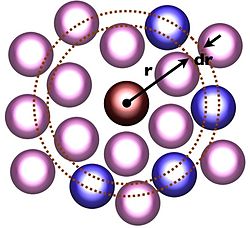
動径分布関数(どうけいぶんぷかんすう、英: radial distribution function)とは、等方的な系(または角度依存性を近似的に無視できる系、球対称な系)の中で、ある物理量の分布が原点からの距離 r のみの関数である場合に、その分布を表す関数である。
非等方的な系に対しては、分布関数を2種類の角度で積分したもので考える[1]。
状況に応じて種々の定義がなされるので注意が必要である。
例[編集]
例えば、ある原子の電子密度を原子核からの距離 r の関数として 4πr2 ρ(r) と表した時、ρ(r) または 4πr2 ρ(r) が動径分布関数と呼ばれる。このとき、全確率は
となる。
この概念が最も有効に用いられる例の一つは、気体・液体・非晶質固体などの原子配置をX線・電子線などの回折法によって解析する場合である。実験的に求められる回折強度に適当な補正を加えたのちフーリエ変換すると、その物質内である原子のまわりの距離 r に他の原子が存在する確率(またはそれと直接に対応する量)を系全体で統計的に平均した動径分布関数が得られる。
例えば、CCl4気体による電子線回折では、1個の分子内でのC-Cl、Cl-Cl原子対の電子散乱能を表す動径分布関数が得られる。それらのピークは分子振動によるゆらぎのために、ほぼガウス分布をしており、その重心は平均核間距離を与える。
貴ガス液体によるX線回折の例では、ある原子から見た他の原子の存在確率を表す動径分布関数が得られる。これは一様な分布のまわりに振動している。分子性液体の場合には、分子の配向に関する統計的平均が加わるので、複雑な解析が必要となる。
別の例として、水素原子の1s関数に対する動径分布関数は次式となる[1]。
ただし a0 はボーア半径である。
参考文献[編集]
- 『物理学辞典』 培風館、1984年
- ^ a b 田中一義; 田中庸裕『物理化学』丸善、2010年、229頁。ISBN 978-4-621-08302-4。


