深さ優先探索
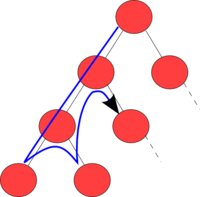
深さ優先探索（ふかさゆうせんたんさく、英: depth-first search, DFS、バックトラック法ともいう）は、木やグラフを探索するためのアルゴリズムである。アルゴリズムは根から(グラフの場合はどのノードを根にするか決定する)始まり、バックトラックするまで可能な限り探索を行う。「縦型探索」とも呼ばれる。
目次 |
概要 [編集]
形式的には、深さ優先探索は、探索対象となる木の最初のノードから、目的のノードが見つかるか子のないノードに行き着くまで、深く伸びていく探索である。その後はバックトラックして、最も近くの探索の終わっていないノードまで戻る。非再帰的な実装では、新しく見つかったノードはスタックに追加される。
深さ優先探索の空間計算量は幅優先探索の空間計算量よりずっと低い。また、分岐を選択するためのヒューリスティックな方法にも向いている。両者の時間計算量は、ノード数とたどる辺の数の合計に比例する。
メモリに載りきらないような大規模なグラフを探索する場合、深さ優先探索は探索木のパスの長さが長くなりすぎて探索が終わらないという問題を抱えている。「訪れたノードを記憶する」という単純な方法は、十分なメモリ量がない場合通用しなくなるのである。これは、木の深さを段階的に増やして探索する反復深化深さ優先探索(en:iterative deepening depth-first search)と呼ばれるアルゴリズムで解決することができる。
下記の図を用いた場合、
グラフの左にある辺が右にある辺より先に選択され、以前訪れたノードを記憶することにより再訪しないとするならば、Aからスタートした深さ優先探索はA, B, D, F, E, C, Gという順番で訪れる。
ここで以前訪れたノードを記憶していない場合、A, B, D, F, E, A, B, D, F, Eと、A, B, D, F, Eのループに捕まって永遠にCやGに到達することはできない。
反復深化はこのループを回避し、上記のように左から右に探索が進むとすると、下記の深さにおいて下記のノードに到達する。
- 0: A
- 1: A (repeated), B, C, E
(反復深化はCをみつけていることに注意。通常の深さ優先探索では見つからない。)
- 2: A, B, D, F, C, G, E, F
(以前Cを見つけていることに注意。Eを別のパスでみつけていることとFでループを見つけていることにも注意。)
- 3: A, B, D, F, E, C, G, E, F, B
このグラフでは深さを増やしていくたびに、アルゴリズムが探索を断念して他の枝に行くまで"ABFE", "AEFB"のループが長くなる。
擬似コード(再帰的) [編集]
dfs(v)
process(v)
mark v as visited
for all vertices i adjacent to v not visited
dfs(i)
Pythonでの実装(再帰しない) [編集]
def depthFirstSearch( start, goal ):
stack = Stack()
start.setVisited()
stack.push( start )
while not stack.empty():
node = stack.top()
if node == goal:
return stack # stack contains path to solution
else:
child = node.findUnvisitedChild()
if child == none:
stack.pop()
else:
child.setVisited()
stack.push( child )
その他 [編集]
dfs(graph G)
{
list L = empty
tree T = empty
choose a starting vertex x
search(x)
while(L is not full)
remove edge (v, w) from end of L
if w not yet visited
{
add (v, w) to T
search(w)
}
}
search(vertex v)
{
visit v
for each edge (v, w)
add edge (v, w) to end of L
}
