ブレイド群

数学において、 $n$ 本の糸のブレイド群(braid group)（組みひも群とも呼ぶ）は、 $B n$ と記し、直感的には幾何学的に描かれる群であり、ある意味で対称群 $S n$ を一般化する。ここに $n$ は自然数であり、 $n > 1$ であれば、 $B n$ は無限群（英語版）(infinite group)である。ブレイド群は、結び目をあるブレイド（組みひも）の閉じた形として表現することができるので、結び目理論に応用を持つ。

はじめに[編集]

直感的な記述[編集]

この導入では（他の値への一般化は容易であると思われるので）、n=4 とする。

4つの黒い点からなる集まりがテーブルの上に2組置かれている状況を考えよう。ただし各々の集まりの中で、黒い点は縦方向に整列しており、また2組の集まりは左右に向かい合って置かれているものとする（下図の黒点部分を参照）。左側の 4点と右側の 4点とを 4本の糸を使って繋ぎ合わせると、左右の4点の集合の間に1：1対応ができる。このように繋がれたものをブレイド（組みひも）と言う。それぞれの糸は他の糸の上や下を通らねばならないことがあり、このことが重要である。例えば、次の 2つの繋ぎ方は異なったブレイドを定める。

　は、

　とは違っている。

他方、「糸を引っ張る」ことにより同じに見えるようになる 2つのブレイドは、同じブレイドとする。

　は、

　と同じブレイドである。

糸はすべて左から右へ移動することとするので、次のような結び目はブレイドとは見なさない。

　をブレイドとは見なさない。

任意の 2つのブレイドは、次の図式に描くように合成することができる。真ん中に現れる 2組の 4点をそれぞれ同一視し、その点で結びついている糸をつなぎ合わせる。

　と、

とを組み合わせると、

　となる。

別の例：

　と、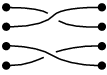

とを組み合わせると、

　となる。

ブレイド $σ$ と $τ$ の合成を、 $στ$ と書くこととする。

4つの糸を持つすべてのブレイドの集合は、 $B 4$ と書かれる。上のブレイドの合成は、実際、群演算である。単位元は4本の水平な糸からなるブレイドであり、あるブレイドの逆元は、そのブレイドの中央の縦線を軸として鏡映反転させたブレイドである。 (例えば、上で述べた最初の2つのブレイドの例は、互いに逆元である。)

数学的な扱い[編集]

上記の直感的なブレイド群の議論を数学的に厳密に扱うには、代数トポロジーにおけるホモトピー的な考え方を用いる必要がある。この考え方では、ブレイド群を配置空間（英語版）(configuration space)の基本群として定義する。このことについては、組みひも理論（英語版）の記事に概説されている。

その代わりに、ブレイド関係式を通じて純代数的にブレイド群を定義することも可能である。その場合ブレイドの図は、直感を助けるため以外には用いてはならないことに注意されたい。

歴史[編集]

ブレイド群は1925年にエミール・アルティン(Emil Artin)により明示的に導入された。、しかし（1974年にウィルヘルム・マグナス（英語版）(Wilhelm Magnus)が指摘しているように^[1])暗にではあるが、ブレイドは、1891年のアドルフ・フルヴィッツ(Adolf Hurwitz)のモノドロミーの論文の中に現れていた。実際、マグナスは、フルヴィッツはブレイド群を配置空間の基本群として解釈していて（組みひも理論を参照）、1962年にラルフ・フォックス（英語版）(Ralph Fox)とレー・ノイヴィルス（英語版）(Lee Neuwirth)により再発見されるまで、この見方をもたらす解釈は失われていた。

基本的性質[編集]

生成元と関係式[編集]

次の 3つのブレイドを考える。


σ₁	σ₂	σ₃

$B 4$ のすべてのブレイドは、これらのブレイドと逆元とを合成として表すことができる。言い換えると、これらの 3つの組みひもは、群 $B 4$ を生成する。このことを見るには、任意の組みひも左端を始点として、左から右へ交点を探すと、糸 $i$ と $i + 1$ が交わったときはいつも糸 $i$ が糸 $i + 1$ の上を通るか下を通るかに従い、 $σ i$ 、あるいは $σ i -1$ と書くことにする。このことを繰り返し右端へ至ると、組みひもは σ とその逆元の積として書き表すことができることが分る。

(i)

σ 1 σ 3 = σ 3 σ 1

,

であることは明らかであることに対し、次の 2つの関係式は全く明らかであるとは言えない。

(iia)

σ 1 σ 2 σ 1 = σ 2 σ 1 σ 2

,

(iib)

σ 2 σ 3 σ 2 = σ 3 σ 2 σ 3

（これらは、一枚の紙の上にブレイドを描くことによりよく理解できる。）ブレイド $σ 1, σ 2, σ 3$ の間にある他の全ての関係は、上の関係式と群の公理から得ることができる。

この例を $n$ 本の糸へ一般化すると、群 $B n$ が、次の表示(presentation)を通して抽象的に定義される。

B_{n}=\left\langle \sigma _{1},\ldots ,\sigma _{n-1}|\sigma _{i}\sigma _{i+1}\sigma _{i}=\sigma _{i+1}\sigma _{i}\sigma _{i+1},\sigma _{i}\sigma _{j}=\sigma _{j}\sigma _{i}\right\rangle \ .

ここに、最初の等式では $1 \leq i \leq n -2$ であり、第二の等式では $| i - j | \geq 2$ である。この表示は、アルティン群（英語版）(Artin group)と呼ばれるブレイド群の一般化を導く。ブレイド関係式として知られている三つ組の恒等式は、ヤン・バクスター方程式（英語版）(Yang–Baxter equation)の理論の中で重要な役目を担う。

その他の性質[編集]

組みひも群 $B 1$ は、自明な群であり、 $B 2$ は無限巡回群 $Z$ であり、 $B 3$ は三葉結び目の結び目群と同型である。特に、この群は、非可換群な無限群である。

$n$ -本の糸の組みひも群 $B n$ は、余剰な糸を最初の $n$ 本の糸のどれとも交差することなく加えることにより、 $(n +1)$ -本の糸のブレイド群 $B n +1$ の部分群として埋め込める。すべての $n \geq 1$ に対するブレイド群の合併は、無限ブレイド群(infinite braid group) $B \infty$ である。

単位元（同一視写像）を除くすべての $B n$ の元は、無限の位数を持っている。すなわち、 $B n$ は捩れを持たない。

$B n$ 上には、デホロノイ順序（英語版）(Dehornoy order)と呼ばれる左不変な全順序が存在する。

$n \geq 3$ に対し、 $B n$ は 2つの生成子を持つ自由群と同型な部分群を含む。

$σ i \mapsto 1$ により定義された準同型 $B n \to Z$ が存在する。従って、たとえば、ブレイド $σ 2 σ 3 σ 1 -1 σ 2 σ 3$ は、 $1 + 1 - 1 + 1 + 1 = 3$ へ写像される。この写像は、ブレイド群のアーベル化に対応している。

ブレイド群の相互関係[編集]

対称群と純粋ブレイド群の関係[編集]

糸がどのように捩れたり交差したりしているかを忘れると、 $n$ 本の糸のブレイドは $n$ 個の元の置換を決める。この対応関係は上への写像であり、合成と整合する。従って、ブレイド群から対称群への全射群準同型 $B n \to S n$ が存在する。ブレイド σ_i ∈ $B n$ の像は、移動 $s i = (i, i +1) \in S n$ である。これらの移動は対称群を生成し、位数 2 のブレイド群の関係式を満たす。この写像は対称群のコクセター群の中へのブレイド群のアルティン表示を変換する。

S_{n}=\left\langle s_{1},\ldots ,s_{n-1}|s_{i}s_{i+1}s_{i}=s_{i+1}s_{i}s_{i+1},s_{i}s_{j}=s_{j}s_{i}{\text{ for }}|i-j|\geq 2,s_{i}^{2}=1\right\rangle .

準同型 $B n \to S n$ の核は、 $B n$ の部分群であり、 $n$ 本の糸の純粋ブレイド群と呼ばれ、 $P n$ と書く。純粋ブレイドは、各々の糸の起点と終点が同様の位置にある。純粋ブレイド群は、短完全系列に適合する。

1\to F_{n-1}\to P_{n}\to P_{n-1}\to 1.

この系列は分裂し、従って純粋ブレイド群は自由群の半直積を繰り返し取ることとして実現される。

$B 3$ とモジュラー群の関係[編集]

$B 3$ は、モジュラー群の普遍中心拡大（英語版）(universal central extension)である。

ブレイド群 $B 3$ はモジュラー群 $PSL(2, Z)$ の普遍中心拡大（英語版）(universal central extension)であり、（位相的な）不変被覆群

{\overline {\mathrm {SL} (2,\mathbf {R} )}}\to \mathrm {PSL} (2,\mathbf {R} )

の中の格子として実現される。

さらに、モジュラー群は自明な中心を持ち、モジュラー群はその中心 $Z (B 3)$ を modulo とする $B 3$ の商群である。同じことであるが、 $B 3$ の内部自己同型(inner automorphism)群と同型である。

ここで、この同型を構成する。

a=\sigma _{1}\sigma _{2}\sigma _{1},\quad b=\sigma _{1}\sigma _{2}

と定義する。ブレイド関係式より、 $a 2 = b 3$ であることが従う後者の積を $c$ で表すことにすると、 $c$ が $B 3$ の中心の中に含まれることを意味するブレイド関係式

\sigma _{1}c\sigma _{1}^{-1}=\sigma _{2}c\sigma _{2}^{-1}=c

を得ることが分る。 $C$ を $c$ により生成された $B 3$ の部分群とすると、 $C \subset Z (B 3)$ であるので、この群は正規部分群であり、商群 $B 3 / C$ をとることができる。 $B 3 / C ≅ PSL(2, Z)$ であることが分り、この同型は明確な形で表すことができる。剰余類 $σ 1 C$ と $σ 2 C$ は次のように写像される。

\sigma _{1}C\mapsto R={\begin{bmatrix}1&1\\0&1\end{bmatrix}}\qquad \sigma _{2}C\mapsto L^{-1}={\begin{bmatrix}1&0\\-1&1\end{bmatrix}}

ここに、 $L$ と $R$ は標準的なスターン・ブロコット木（英語版）(Stern-Brocot tree)の上の左と右の移動である。これらの移動はモジュラー群を生成することがよく知られている。

言い替えると、モジュラー群の共通な表示(presentation)は、

\langle v,p\,|\,v^{2}=p^{3}=1\rangle

であり、ここに、

v={\begin{bmatrix}0&1\\-1&0\end{bmatrix}},\qquad p={\begin{bmatrix}0&1\\-1&1\end{bmatrix}}

である。

$a$ から $v$ への写像と $b$ から $p$ への写像は、全射群準同型 $B 3 \to PSL(2, Z)$ である。

$B 3$ の中心は、 $C$ に等しく、 $c$ が中心に含まれるという事実の結果であり、モジュラー群は自明な中心を持ち、上の全射準同型は核 $C$ を持つ。

写像類群とブレイドの分類への関係[編集]

ブレイド群 $B n$ は、 $n$ 個の穴のあいた穴あき円板の写像類群（英語版）(mapping class group)と同型であることを示すことができる。これは境界円板の各穴を糸で繋げるというイメージで最も容易に可視化される。即ち、写像類群の元は穴空き円板の穴を入れ替えるので、これを糸のホモトピー、つまり糸のブレイディングと見做すことができる。

この写像類群というブレイドの解釈を通し、各々のブレイドは、周期的で規約な、あるいは、擬アノソフ的なニールセン・サーストン分類（英語版）(Nielsen-Thurston classification)として分類することができる。

結び目理論と繋がり[編集]

ブレイドが与えられ、最初の左側の点の集まりから右の点の集まりへ新しい糸を使って繋ぎ合わせることができ、第一の図式の左側の点と第二の図式の右側の点が関係付けられる（新しく糸でブレイドを作成することなく）るとすると、絡み目や、結び目が得られる。組み紐理論のアレクサンダーの定理は、逆もまた成立するという定理であり、すべての結び目と絡み目は少なくとも一つのブレイドから得られる形となる。そのようなブレイドは、絡み目を切断することにより得ることができる。ブレイドは生成子 $σ i$ での語(word)として与えられるので、計算機プログラムで結び目を扱う方法として採用されている。

計算する場合[編集]

ブレイド関係式の語の問題（英語版）(word problem)は、有効に解くことができ、 $B n$ の元を生成子 $σ 1, ..., σ n -1$ の項として正規化して表す表現方法が存在する。（本質的には、ブレイドの正規化形式を計算することは、上の図の第二の図式で説明されているように、糸の引っ張ることの代数的な類似物である。）GAP (数式処理システム)は、元がこれらの生成子の項で与えられれば、 $B n$ の計算を実行することができる。また、GAP3 の CHEVIE と呼ばれるシステムでは、特別な種類のブレイド群をサポートしている。語の問題は、ローレンス・クラマー表現（英語版）(Lawrence-Krammer representation)を通した有効に解くことができるかという問題でもある。

それにもかかわらず、ブレイド群についての計算問題は非常に困難な問題があるため、暗号理論への応用が提案されている。

ブレイド群の作用[編集]

置換による対称群の作用と類似して、様々な数学的設定において、対象の $n$ -個の組の上、あるいは、「ツイスト」を持つ $n$ -重のテンソル積上へ、ブレイド群が自然に作用する。 $G$ を任意の群、 $X$ を $G$ の元のすべての $n$ -個の組の集合で、それらの積が $G$ の単位元となる集合とすると、 $B n$ は、次の形で $X$ の上へ作用する。

\sigma _{i}\left(x_{1},\ldots ,x_{i-1},x_{i},x_{i+1},\ldots ,x_{n}\right)=\left(x_{1},\ldots ,x_{i-1},x_{i+1},x_{i+1}^{-1}x_{i}x_{i+1},x_{i+2},\ldots ,x_{n}\right).

このように、元 $x i$ と $x i +1$ の場所を交換し、加えて、 $x i$ が $x i +1$ に対応する内部自己同型(inner automorphism)によりツイストされる — これは、 $x$ の成分の積が単位元のままであることを保証する。これはブレイド群の関係式を満たすことが確認され、実際、この式が $X$ 上の $B n$ の群作用を定義する。別な例として、ブレイドモノイダル圏（英語版）(braided monoidal category)は、ブレイド群の作用を持つモノイダル圏である。そのような構造は、現代の数理物理学で重要な役目を果し、量子結び目不変量を導く。

表現[編集]

ブレイド群 $B n$ の元は、行列によりより具体的に表現することができる。一つの古典的なそのような表現は、ブーラウ表現（英語版）(Burau representation)であり、そこでは行列要素は一変数のローラン多項式である。ブーラウ表現が忠実であるか否かは長い間問題となっていたが、解答として $n \geq 5$ に対しては否定的であることが判明した。さらに一般的に、ブレイド群が線型であるか否かは大きな未解決問題であった。1990年、ラス・ローレンス（英語版）(Ruth Lawrence)は、複数のパラメータに依存するより一般的な「ローレンス表現」の族を記述した。1996年、ナヤカ(C. Nayak)とフランツ・ウィルチェック(Frank Wilczek)は、 $SO(3)$ の類似を考え、ブレイド群の射影表現がような分数量子ホール効果でのある擬粒子に関する物理的意味を持っていることを提唱した。2001年頃、ステファン・ビゲロー(Stephen Bigelow)とダン・クラマー(Daan Krammer)は、独立に、すべてのブレイド群は線型であることを証明した。彼らの仕事には、変数 $q$ と $t$ に依存しない次元 $n (n -1)/2$ のローレンス・クラマー表現（英語版）(Lawrence–Krammer representation)が使われた。これらの変数を適切に特殊化することにより、ブレイド群 $B n$ は複素数上の一般線型群の部分群として実現することができる。

無限生成ブレイド群[編集]

この考え方を無限本の糸からなるブレイドへ一般化するには、多数の方法がある。最も簡単な方法はブレイド群の帰納極限を取ることであり、そこでは結び付けている写像 $f : B n \to B n +1$ は、 $B n$ の $n -1$ 個の生成子を、 $B n +1$ の最初の $n -1$ 個の生成子へ写す（つまり、自明な糸をひとつ付け加える）。ファベル(Fabel)は、完備化が異なる構造の群となる群を結果として得れるような、2つの位相が存在することを示した。ひとつは、非常におとなしい群で、無限個の穴のあいた円板の写像類群（英語版）(mapping class group)に同型 — 単位円板の境界に極限を持つように穴の開いた離散集合である。

第二の群は、有限ブレイド群と同じと考えられる。各々の点 $(0, 1/ n)$ とすべてのブレイドの集合に糸を配置すると、そこではブレイドが点 $(0, 1/ n, 0)$ から点 $(0, 1/ n, 1)$ への経路の集まりとして定義され、従って、函数が終点上の置換となり、このワイルドな群に同型となる。興味深い事実は、この群の中の純ブレイド群が、有限ブレイド群 $P n$ の逆極限と、ヒルベルトの立方体(Hilbert cube)から次の式で表される集合をマイナスした空間の基本群の双方と同型となるという事実である。

\{(x_{i})_{i\in {\mathbb {N}}}\mid x_{i}=x_{j}{\text{ for some }}i\neq j\}.

脚注[編集]

^ Magnus, Wilhelm (1974). “Braid groups: A survey”. In Newman M.F.. Proceedings of the Second International Conference on the Theory of Groups. Lecture Notes in Mathematics. 372. Springer. pp. 463–487. doi:10.1007/978-3-662-21571-5_49. ISBN 978-3-540-06845-7 2021年9月29日閲覧。

参考文献[編集]

Deligne, Pierre (1972), “Les immeubles des groupes de tresses généralisés”, Inventiones Mathematicae 17 (4): 273–302, doi:10.1007/BF01406236, ISSN 0020-9910, MR0422673

さらに先の書籍[編集]

Birman, Joan; Brendle, Tara E. (26 February 2005), Braids: A Survey, arXiv:math.GT/0409205 . In Menasco & Thistlethwaite 2005
Carlucci, Lorenzo; Dehornoy, Patrick; Weiermann, Andreas (23 November 2007), Unprovability results involving braids, arXiv:0711.3785
Kassel, Christian; Turaev, Vladimir (2008), Braid Groups, Springer, ISBN 0-387-33841-1
Menasco, W.; Thistlethwaite, M., eds. (2005), Handbook of Knot Theory, Elsevier, ISBN 0-444-51452-X

外部リンク[編集]

Braid group - PlanetMath.org（英語）
CRAG: CRyptography and Groups at Algebraic Cryptography Center Contains extensive library for computations with Braid Groups
Fabel, P. (2005), “Completing Artin's braid group on infinitely many strands” (PDF), Journal of Knot Theory and its Ramifications 14 (8): 979–991, doi:10.1142/S0218216505004196, オリジナルの2006年1月9日時点におけるアーカイブ。
Fabel, P. (2006), “The mapping class group of a disk with infinitely many holes” (PDF), Journal of Knot Theory and its Ramifications 15 (1): 21–29, doi:10.1142/S0218216506004324, オリジナルの2005年1月29日時点におけるアーカイブ。
Chernavskii, A.V. (2001), “Braid theory”, in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
Stephen Bigelow's exploration of B5 Java applet.
Nayak, C.; Wilczek, F. (1996), $2n$ Quasihole States Realize $2^{n-1}$-Dimensional Spinor Braiding Statistics in Paired Quantum Hall States, arXiv:cond-mat/9605145, doi:10.1016/0550-3213(96)00430-0 — connection of projective braid group representations to the fractional quantum Hall effect
Presentation for FradkinFest by C. V. Nayak [1]^{[リンク切れ]}
Read, N. (2002), Nonabelian braid statistics versus projective permutation statistics, arXiv:hep-th/0201240 — criticism of the reality of Wilczek-Nayak representation
Lipmaa, Helger, Cryptography and Braid Groups page, オリジナルの2009年8月3日時点におけるアーカイブ。
Braid group: List of Authority Articles on arxiv.org.

[1] Magnus, Wilhelm (1974). “Braid groups: A survey”. In Newman M.F.. Proceedings of the Second International Conference on the Theory of Groups. Lecture Notes in Mathematics. 372. Springer. pp. 463–487. doi:10.1007/978-3-662-21571-5_49. ISBN 978-3-540-06845-7 2021年9月29日閲覧。

[1]

表話編歴結び目理論（結び目と絡み目）
双曲（英語版）	8の字 (4₁) Three-twist（英語版） (5₂) Stevedore（英語版） (6₁) 6₂（英語版） 6₃（英語版） Endless（英語版） (7₄) Carrick mat（英語版） (8₁₈) Perko pair（英語版） (10₁₆₁) (−2,3,7) プレッツェル（英語版） (12n242) ホワイトヘッド（英語版） (52 1) ボロミアン環 (63 2) L10a140（英語版）
サテライト（英語版）	合成結び目（英語版） Granny（英語版） Square（英語版）結び目の和（英語版）
トーラス	自明 (unknot) (0₁) 三つ葉 (3₁) Cinquefoil（英語版） (5₁) Septafoil（英語版） (7₁) 自明 (unlink) (02 1) ホップ（英語版） (22 1) ソロモン（英語版） (42 1)
結び目不変量	交代アルフ不変量（英語版） Bridge number（英語版） 2-bridge Brunnian（英語版）カイラリティ（英語版）可逆（英語版） Crosscap number（英語版）交点数有限型不変量双曲体積ホヴァノフホモロジー種数（英語版）結び目群絡み目群（英語版）絡み数結び目多項式（英語版）アレクサンダーブラケット HOMFLY ジョーンズカウフマンプレッツェル（英語版）素（英語版）（一覧（英語版）） Stick number（英語版） 3彩色可能性結び目解消数（英語版）と解消問題（英語版）
記法と演算（英語版）	Alexander–Briggs の記法（英語版）コンウェイの記法（英語版）ドウカーの記法 Flype（英語版） Mutation（英語版）ライデマイスター移動スケイン関係式 Tabulation（英語版）
その他	アレクサンダーの定理 Berge（英語版）組み紐理論（英語版）コンウェイの球面（英語版）補空間二重トーラス（英語版） Fibered（英語版）結び目 (一般項目) 結び目と絡み目の一覧（英語版）リボン（英語版）スライス（英語版）結び目の和テイト予想 Twist（英語版）野性の（英語版） (Wild) Writhe 手術理論（英語版）
カテゴリコモンズ