食事する暗号学者の問題

出典: フリー百科事典『ウィキペディア（Wikipedia）』

食事する暗号学者の問題[1] (dining cryptographers problem)とは、匿名による情報発信法やその匿名性の証明に関する問題である。

問題[編集]

3人以上の暗号学者達が円卓で食事を取っていた。

そこにウェイターがやって来て匿名の何者かが彼ら全員分の食事代を支払ったと学者達に伝えた。学者のうちの誰かが払ったのかもしれないし、学者達の雇い主であるNSA(アメリカ国家安全保障局)が支払ったのかもしれない。どちらが支払ったのか知りたいが、もし学者のうちの誰かが支払ったのなら、匿名で支払ったという意思を尊重したい。

どちらが支払ったのか、支払った学者を特定することなく知る方法はあるだろうか？

解決法: 食事する暗号学者のプロトコル[編集]

例として4人の場合を考える。 まず右隣りの学者との間で、メニューの裏でこっそりコインをトスする。 結果は2人だけで共有し、他の学者には秘密にする。

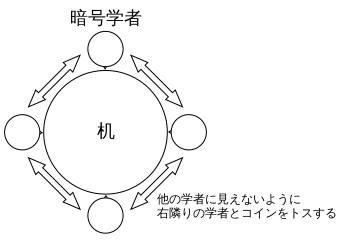
次に対面の学者とも同様にコインをトスし、秘密を共有する。

この時点で各学者は右隣り、左隣り、対面の3人の学者とのコイントスの結果を持っている。 そして各学者は3回のコイントスの結果、表が出た回数が奇数であったか偶数であったか全員に向かって宣言する。 ただし食事代を支払った学者だけは反対の結果を宣言する。

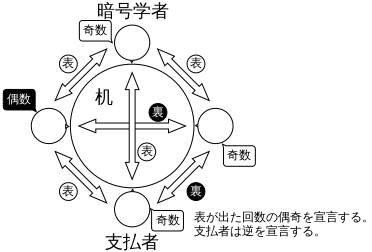
この時点で4人分の宣言の結果が揃っている。 もし4人の中で「奇数」と宣言した学者の数が偶数であれば、NSAが支払ったという情報が得られる。そうでない場合は学者の1人が支払ったという情報が得られるが、この場合、4人のうち誰が支払ったのかについては、支払った本人以外は知ることはない[1]。

学者の人数が一般のnの場合も同様にn-1人とコインをトスすればよい。

このプロトコルは、デビッド・チャウム (David Chaum)によりDC-net (Dining Cryptographers NETwork)と名付けられている([1]3節)。

匿名ネットワーク[編集]

上で示したプロトコルでは、食事代を支払った（高々）1人の暗号学者がビット"1"を送信し、それ以外の学者は何も送信しない（あるいはビット"0"を送信した）とみなすことができる。誰かが"1"を送信した事実を全員が知ることができ、同時に送信者の匿名性を保つこともできるため、匿名ネットワークとして使うことができる。

もし、2ビット以上のメッセージを発信したい場合は、一連の動作を複数回繰り返せばよい。繰り返しは直列的に行う必要はなく、並行して行える。

衝突回避[編集]

同時に二人以上がメッセージを発信した場合、複数のメッセージがまじりあって排他的論理和が結果として得られる。これを衝突と呼ぶ。チャウムは、2つの衝突を回避する方法を示している([1]2.2節)。

1つは、メッセージの発信者が衝突を検知したら、無作為な時間だけ待ってから再送するという方法(CSMA/CD)である。

もう1つは、通信枠の予約(slot reservation)を使った回避方法である。この場合、mビットを1ブロックとしてまとめて送信するCD-netを使う。まず、情報発信する参加者は1からmの間の数iを無作為に選び、i番目のビットのみが1で、それ以外が0であるようなmビットのビット列(0 0 ... 1 ... 0 0)を決める。そして、最初のブロックの送信時には、この(0 0 ... 1 ... 0 0)を送信する。最初のブロックで衝突が起こらないことを確認したならば、次のブロックで、ブロックのi番目のビットに自分の送りたいメッセージを埋め込んで発信する。（それ以外のビットは0とする。）このようにすれば、同時に複数人が、異なるスロットを使ってメッセージを発信することができる。 ただし、誕生日のパラドックスがあるため、衝突確率を一定以下に保つためには、ブロックのサイズmを参加者数の自乗に比例させる必要がある([1]2.5節)。

安全性[編集]

食事する暗号学者のプロトコルでは、1人を除く全員が結託したときに限り発信者を特定できる([1]1.3節)。

これを一般化して自分以外の全員と秘密を共有するのではなく、限られた参加者とのみ秘密を共有する場合を考える。すると各参加者を端点とし、秘密の共有関係を辺としたグラフが考えられる。

ここでグラフからいくつかの辺を取り除く場合を考える。このとき各連結成分を、取り除いた辺の集合に対する匿名性集合(anonymity set)という([1]1.1節)。

そして複数の参加者が結託して発信者を特定しようとした場合、結託した参加者に接する辺をグラフから取り除く。このとき結託した参加者は各匿名性集合ごとに情報発信した参加者の有無を得られるが、匿名性集合の中の発信者は特定できない([1]1.1節, 1.4節)。

特別な場合として、グラフが円構造の場合、両隣の2人が結託した場合、その発信者の匿名性は失なわれる([1]2.3節)。

対妨害性[編集]

故意や実装のバグによりノイズを流す参加者がいると他の参加者による情報発信が妨害されてしまう。これに対し、妨害者と接する辺を少しずつ減らしていく方法が提唱されている([1]2.5節)。

ミックスネットワークとの比較[編集]

[1]の著者による匿名情報発信技術の1つであるミックスネットワークの匿名性は、公開鍵暗号技術に依存しているため計算量的安全性しか持たない。一方で食事する暗号学者のプロトコルは鍵を安全に交換した場合情報理論的安全性を持つ([1]3節)。

関連項目[編集]

参考文献[編集]

  1. ^ a b c d e f g h i j k l m David Chaum. The Dining Cryptographers Problem: Unconditional Sender and Recipient Untraceability. J. Cryptology 1(1), 1988, pp. 65-75.
  2. ^ Timothy C. May. [1] DC-Nets. Cyphernomicon. 1994. section 13.4.8
「https://ja.wikipedia.org/w/index.php?title=食事する暗号学者の問題&oldid=85144819」から取得