行列
数学の線型代数学周辺分野における行列(ぎょうれつ、英: matrix)は、数や記号や式などを縦と横に矩形状に配列したものである。
概要[編集]
行・列[編集]
横に並んだ一筋を行(row)、縦に並んだ一筋を列(column)と呼ぶ。
例えば、下記のような行列
は2つの行と3つの列によって構成されているため、(2,3)型または2×3型の行列と呼ばれる。
成分[編集]
書き並べられた要素は行列の成分と呼ばれ、行列の第 i 行目、j 列目の成分を特に行列の (i, j) 成分と言う。行列の (i, j) 成分はふつう ai j のように二つの添字を単に横並びに書くが、誤解を避けるために添字の間にコンマを入れることもある。また略式的に、行列 A の (i, j) 成分を指定するのに Ai j という記法を用いることもある。
和・積[編集]
行列の和は、行の数と列の数が同じ行列において、成分ごとの計算によって与えられる。
行列の積の計算はもっと複雑で、2つの行列がかけ合わせられるためには、積の左因子の列の数と右因子の行の数が一致していなければならない。
行列の応用[編集]
一次変換[編集]
行列の応用として代表的なものは一次変換の表現で、これは f (x) = 4x のような一次関数を一般化したものである。例えば、三次元空間におけるベクトルの回転は一次変換にあたり、R が回転行列で v が空間の点の位置を表す列ベクトル(1 列しかない行列)であるとき、それらの積 Rv は回転後の点の位置を表す列ベクトルを表現している。また 2つの行列の積は、2つの一次変換の合成を表現するものとなる。
線型方程式系[編集]
また、その他の応用としては、線型方程式系の解法が挙げられる。行列が正方行列であるとき、そのいくつかの性質は、行列式を計算することによって知ることができる。例えば、正方行列において、行列式の値が非零となることは、それが正則であるための必要十分条件である。固有値と固有ベクトルは一次変換の幾何学に対する洞察を与える。
科学[編集]
行列の応用は科学的な分野の大半に及ぶ。
特に物理学において行列は、古典力学、光学、電磁気学、量子力学などにおける様々な物理現象のモデル化と研究に利用される。
運動学やロボット工学では座標変換や姿勢制御などに行列が使われる。特に同次座標変換のため、2次元の座標変換では3×3行列が、3次元の座標変換では4×4行列が使われることが多い。コンピュータグラフィックスにも応用されている(後述)。
確率論や統計学、確率行列において行列は確率の組を表現するのに用いられ、例えば、これはGoogle検索におけるページランクのアルゴリズムで使われている。
行列の微積分は、古典的な解析学における微分や指数関数の概念を高次元へ一般化するものである。
経済学では経済上の関係のシステムを説明するのに行列が用いられる。
アルゴリズム[編集]
行列計算の効率的なアルゴリズムの研究は数値解析における主要な分野であり、これは何世紀にもわたるもので、今日でも研究領域が広がっている。
行列の分解は、理論的にも実用的にも計算を簡単化するもので、そのアルゴリズムは正方行列や対角行列などといった行列の特定の構造に合わせて仕立てられており、有限要素法やそのほかの計算を効率的に処理させる。
惑星運動論や原子論では無限次行列が現れる。
無限次行列の簡単な例としては、関数のテイラー級数に対して作用する微分作用素を表す行列がある。
素朴な定義[編集]
記法[編集]
行列は数または数を表わす文字から成る要素 (英: element) を矩形状に書き並べて、大きな丸括弧(あるいは角括弧)で括った形に書かれる。ここで文字送りの方向(横)の並びを行 (英: row) といい、行送りの方向(縦)の並びを列 (英: column) と呼ぶ[1]。例えば
は 2 つの行と 3 つの列を持つ行列である。行列自身は、ふつうはアルファベットの大文字イタリック(しばしば太字[注釈 1])で表し、その要素は対応する小文字に二つの添字を付けたもので表す(略式的に行列を表す大文字に添字を付けたものを用いることもあるが、その場合小行列の記号と紛らわしい)。つまり一般の m 行 n 列の行列を
のように書く。
成分[編集]
書き並べられた要素は行列の成分 (英: entry, component) と呼ばれる[1]。成分が取り得る値は(さまざまな対象を想定できるが)大抵の場合はある体または可換環 K の元であり、このとき K 上の行列 (英: matrix over K) という。特に、K が実数全体の成す体 R であるとき実行列と呼び、複素数全体の成す体 C のとき複素行列と呼ぶ。
一つの成分を特定するには、二つの添字が必要である。行列の第 i 行目、j 列目の成分を特に行列の (i, j) 成分と呼ぶ[1]。例えば上記行列 A の (1, 2) 成分は a1 2 である。行列の (i, j) 成分はふつう ai j のように二つの添字を単に横並びに書くが、誤解を避けるために添字の間にコンマを入れることもある。例えば 1 行 11 列目の成分を a1,11 と書いてよい。また略式的には、行列 A の (i, j) 成分を指定するのに Ai j という記法を用いることがある。この場合、例えば積(後述)A B の (i, j) 成分を (A B)i j と指定したりできるので、これで記述の簡素化を図れる場合もある。
型[編集]
行列に含まれる行の数が m, 列の数が n である時に、その行列を m 行 n 列行列や m × n 行列、m n 行列などと呼ぶ[1]。行列を構成する行の数と列の数の対を型 (英: type) あるいはサイズという。したがって m 行 n 列行列のことを (m, n) 型行列などと呼ぶこともある[1]。K 上の m × n 行列の全体は Km×n, Km,n や Mat(m, n; K), Mm×n(K) などで表される。
1つの列を持つ行列を列ベクトル、1つの行をもつ行列を行ベクトルと呼ぶ。例えば行列
に対して、[a1 1
a2 1] , [a1 2
a2 2] はその列ベクトル、[a1 1 a1 2], [a2 1 a2 2] はその行ベクトルである。
行と列の数が同じである行列は正方行列と呼ばれる。無限の行または列をもつ行列を無限次行列と呼ぶ。プログラミングにおいて行または列を持たない行列を考えると便利となることがしばしばあるが、このような行列を空行列と呼ぶ。
| 名前 | 型 | 例 | 説明 |
|---|---|---|---|
| 行ベクトル | 1 × n | 1つの行を持つ行列。ベクトルを表すのに使われることがある。 | |
| 列ベクトル | n × 1 | 1つの列を持つ行列。ベクトルを表すのに使われることがある。 | |
| 正方行列 | n × n | 行と列の数が同じである行列。鏡映や回転、せん断のようなベクトル空間の線形変換を表すのに使われることがある。 |
厳密な定義[編集]
行列は二重に添字づけられた族であり、添字の各対 (i, j) に成分 aij を割り当てる二変数写像
である。例えば添字の対 (1, 2) には写像の値として a12 が割り当てられる。値 aij は行列の i-行 j-列成分であるといい、m および n はそれぞれ行および列の数を意味する。写像としての行列の定義と行列が表す線型写像とを混同してはならない。
K に成分を持つ m × n 行列の全体は、したがって配置集合
であり、省略形として Km×n(あるいはやや稀だが mKn)や M(m×n; K) などと書くことの一つの根拠になる。
行の数と列の数が一致するような行列は正方行列と呼ばれる。
ただ一つの列を持つ行列は列ベクトル、ただ一つの行を持つ行列は行ベクトルと呼ばれる。Kn のベクトルは、文脈によって行ベクトル空間 K1×n または列ベクトル空間 Kn×1 の元を表すのにも用いられる。
歴史[編集]
線型方程式の解法における応用に関して、行列は長い歴史を持つ。紀元前10世紀から紀元前2世紀の間に書かれた中国の書物『九章算術』は連立方程式の解法に行列を用いた最初の例であるといわれ[3]、それには行列式の概念が含まれていた。1545年にイタリアの数学者ジェロラモ・カルダーノは『偉大なる術(アルス・マグナ)』を著し、この方法をヨーロッパに持ち込んだ。日本の関孝和は1683年に連立方程式の解法として同様に行列による方法を用いている[4]。ドイツのヨハン・デ・ウィットは1659年の著書 Elements of Curves において行列の変形について説明している。1700年から1710年にかけてドイツのライプニッツは50以上の異なる体系を用いて行列の使い方を発表した。クラメルが有名な公式を生み出すのは1750年のことである。
行列論の初期においては、行列よりも行列式のほうに非常に重きが置かれており、行列式から離れて現代的な行列の概念と同種のものが浮き彫りにされるのは1858年、ケイリーの歴史的論文 Memoir on the theory of matrices(「行列論回想」)においてである[5][6]。用語 "matrix"(ラテン語で「生み出すもの」の意味の語に由来)[7]はシルベスターが導入した。シルベスターは行列を、(今日小行列式と呼ばれる)もとの行列から一部の行や列を取り除いて得られる小行列の行列式として、たくさんの行列式を生じるものとして理解していた[注釈 2]。1851年の論文でシルベスターは
I have in previous papers defined a "Matrix" as a rectangular array of terms, out of which different systems of determinants may be engendered as from the womb of a common parent. (以前の論文で、項を矩形状に並べた配列として定義した "Matrix" は、そのうちで異なる行列式の体系を生み出す共通の親としての母体である。)
と説明している[8]。 行列式の研究はいくつかの流れから生じてきたものである[9]。数論的な問題はガウスが二次形式(つまり、のような数式)の係数と三次元の線型写像を行列に結び付けたことに始まり、アイゼンシュタインがこれらの概念をさらに進めて、現代的な用語でいえば行列の積が非可換であることなどを指摘した。コーシーは行列 の行列式として、多項式
(ここで ∏ は条件を満たす項の総乗を表す)の冪 a j
k を ajk で置き換えたものという定義を採用し、それを用いて行列式についての一般的な主張を証明した最初の人である。コーシーは1829年に、対称行列の固有値が全て実数であることも示している[10]。ヤコビは、幾何学的変換の局所的あるいは無限小のレベルでの挙動を記述することができる関数行列式(後にシルベスターが「ヤコビ行列式」と呼んだ)の研究を行った。クロネッカーの Vorlesungen über die Theorie der Determinanten[11] とワイエルシュトラスの Zur Determinantentheorie[12] はともに1903年に出版された。前者は、それまでのコーシーの用いた公式のような具体的な手法とは反対に、行列式を公理的に扱ったものである。これを以って、行列式の概念がきっちりと確立されたと見なされている。
多くの定理は、初めて確立されたときには小さいサイズの行列に限った主張として示された。例えばケーリー=ハミルトンの定理は、ケイリーが先述の回想録において 2 × 2 行列に対して示し、ハミルトンが 4 × 4 行列に対して証明して、その後の1898年にフロベニウスが双線型形式についての研究の過程で任意次元に拡張した。また、19世紀の終わりに、(ガウスの消去法として今日知られるものを特別の場合として含む)ガウス–ジョルダン消去法をジョルダンが確立し、20世紀の初頭には行列は線型代数学の中心的役割を果たすようになった[13]。前世紀の超複素数系の分類にも行列の利用が部分的に貢献した。
ハイゼンベルク、ボルン、ジョルダンらによる行列力学の創始は、行または列の数が無限であるような行列の研究へ繋がるものであった[14]。後にフォン・ノイマンは、(大体無限次元のユークリッド空間にあたる)ヒルベルト空間上の線型作用素などの関数解析学的な概念をさらに推し進めることにより、量子力学の数学的基礎を提示した。
行列の演算[編集]
基本演算[編集]
加法[編集]
二つの行列は、それが同じ型を持つならば互いに加えることができ、この算法を行列の加法、演算の結果を和と言う[15]。異なる型の行列に対しては和は定義されない。つまり、m 行 n 列の行列同士の和を、成分ごとの和
で定める[15]。
例えば
である。
線型代数学において成分はふつう(実数や複素数の全体のような)体であり、この場合の行列の加法は、結合的かつ可換であり、また単位元として零行列
を持つ[15]。一般に、これらの三性質を満たす代数系に成分を持つ(同じ型の)行列の全体は、やはりこれらの性質を満たす。
スカラー倍[編集]
行列の各成分に一つのスカラーを掛けることにより、任意の行列のスカラー倍
が定義される[15]。例えば、
である。
スカラー乗法が意味を持つためには、スカラー λ と行列の成分が同じ環 (K, +, ·, 0) からとった元であるべきであり、このとき m × n 行列の全体 Km×n は、左 K-加群(K が体ならばベクトル空間)になる。ベクトル空間(あるいは自由加群)としての Km×n は m n 次元数ベクトル空間 Km n と同型である。
乗法[編集]
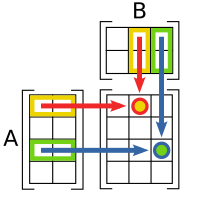
行列の積を初めて定義したのはケイリーである。行列の積は狭い意味での二項演算(即ち、台とする集合 X に対して X × X → X なる写像を定めるもの)ではない。l × m 行列 A と m × n 行列 B の積は l × n 行列となり、C = A B の (i, j) 成分 ci j は、
で与えられる[16]。
例えば、
である。
- 行列の積は可換でない
- 即ち一般にはとなることが両辺が定義される場合 (l = n) であっても起こり得る。さらに m = n(= l) のとき、つまり両辺が正方行列同士の積であれば両辺とも定義されるが、その場合でも一般には両者は異なる[16]。
正方行列に関して行列の乗法は特別な役割を持つ。環 R 上の正方行列全体 Rn×n は行列の加法と乗法に関して、ふたたび環を成すのである。環 R が単位的(つまり単位元 1 を持つ)ならば、単位行列
は行列の積に関する単位元となり、環 Rn×n もまた単位的となる。しかし、n > 1 のとき、この環は(基礎環 R が可換環であっても)可換環でない。
行列が区分行列に分解されるとき、そのような行列の積は、それらのブロックが適当なサイズならば、ブロック成分ごとに積を計算することができる。例えば
である。ここで E2 は二次の単位行列、右辺の 0 は全ての成分が 0R(基礎環 R の零元)であるような適当なサイズの行列である。
転置[編集]
m × n 行列 A = [ai j] の転置とは n × m 行列 tA = [aj i], 即ち
である[18]。これはもとの行列の各列を各行に持つ行列であり、主対角成分 a1 1, a2 2, … に関して折り返したものになっている。
転置行列は以下の計算規則に従う[18]:
行列式[編集]
n × n 行列 A = [ai j] の行列式とは、
で定義される数である[19]。これは行列の固有値の積と一致し、det(En) = 1, det(A B) = det(A) det(B) などが成り立つ。
ランク[編集]
行列 A のランクまたは階数とは、この行列の列ベクトルの中で線型独立なものの最大個数であり、また 行ベクトルの中で線型独立なものの最大個数とも等しい[20]。あるいは A の表現する線型写像の像の次元と言っても同じである[21]。階数・退化次数の定理は、行列の核に階数を加えると、その行列の列の数に等しいことを述べるものである[22]。
トレース[編集]
n × n 行列 A = [ai j] のトレースまたは跡とは、その対角線上にある成分の和
のことである[23]。これは tr(A B) = tr(B A) を満たし[23]、行列のトレースはその固有値の和に等しい。
内積とノルム[編集]
K-加群としての Mm×n(K) はまた、行列の積 tA B のトレース
を内積に持つ。K = R のとき、これはユークリッドノルムを導き、Mm×n(R) は m n-次元ユークリッド空間 Km n になる。この内積空間において、対称行列全体の成す部分空間と歪対称行列全体の成す部分空間とは互いに直交する。即ち、A が対称, B が歪対称ならば ⟨A, B⟩ = 0 が成り立つ。同様に K = C の場合には、Mm×n(C) は
(ただし、上付きのバーは複素共軛)をエルミート内積として複素ユニタリ空間を成す(この内積をヒルベルト・シュミット内積と呼ぶ)。この内積はフロベニウスノルムを導き、Mm×n(C) はバナッハ空間となる。
その他の演算[編集]
差[編集]
任意の行列 B に対し、その成分をそれぞれの成分の加法逆元に全て取り換えた行列を −B と書けば、同じサイズの行列 A, B の和 A + (−B) を A − B と略記して差を定めることができる[注釈 3]。より強く、スカラー乗法が定義される場合には、特にスカラー (−1)-倍は (−1)B = −B を満たすのだから、和とスカラー倍を使って差を定義することもできる。
とすればよい.
べき乗[編集]
n × n の正方行列 A に対して行列のべき乗は An (ここで n は実数) と書かれる[24]。
行列 A が対角化可能であれば、An = (P−1DP)n = P−1DnP として容易に計算できる。
ベクトルの二項積[編集]
v と w を n × 1 の列ベクトルとすると、v と w との間に行列の積は定義されないが、tv w および v tw は行列の積として定義することができる。前者は 1 × 1 行列であり、これをスカラーと解釈すれば、v と w との標準内積 ⟨v, w⟩ に他ならない。いっぽう後者は、階数 1 の n × n 行列で、v と w との二項積 v w あるいはテンソル積 v ⊗ w と呼ばれる。
行列の三項積[編集]
可換環 K 上の m × n 行列の全体 Mm×n(K) は加法とスカラー倍について K-加群を成すばかりでなく、その上の三項演算
を定義することができる。これと同様の方法で得られる三重線型な三項系(三項積)の一般論は、ジョルダン環あるいはリー環の理論とかかわりを持つ[25]。
定義されない演算[編集]
以下のような計算は定義されないため実行してはならない[26]。
行列の分解[編集]
行列を2つあるいは3つの行列の積に因数分解するには以下の方法が知られている。
- LU分解 - 正方行列Aを下三角行列と上三角行列の積に分解。 A = LU
- コレスキー分解 - 正値対称行列(またはエルミート行列)Aを下三角行列と上三角行列の積に分解。 A = U*U
- QR分解 - (m,n)行列を直交行列(またはユニタリ行列)Qと上三角行列Rに分解 A = QR
- 固有値分解 -
- 特異値分解 - (m,n)行列を直交行列(またはユニタリ行列)U,Vと対角行列Dに分解 A = UDV*
様々な行列[編集]
行列サイズによる分類[編集]
行列成分が特別な形の行列[編集]
作用素による作用を受けた行列[編集]
対称性がある行列[編集]
群を構成する行列[編集]
線型写像[編集]

行列とその乗法は、これを一次変換(つまり線型写像)と関連付けるとき、その本質的な特徴が浮き彫りになる。
- 線型写像の行列表現
- m × n 行列 A から線型写像 Rn → Rm が各ベクトル x ∈ Rn を行列としての積 Ax ∈ Rm へ写すものとして定まる。逆に、各線型写像 f: Rn → Rm を生じる m × n 行列 A は一意的に決まる。陽に書けば、A の (i, j)-成分は、f(ej) の第 i-成分である。ただし ej = (0, …, 0, 1, 0, …, 0) は第 j-成分だけが 1 で他が全部 0 の単位ベクトルである。
このとき、行列 A は線型写像 f を表現すると言い、A を f の変換行列または表現行列と呼ぶ。
例えば 2 × 2 行列
は、単位正方形を (0, 0), (a, b), (a + c, b + d), (c, d) を頂点とする平行四辺形に写すものと見做すことができる。この平行四辺形は、単位正方形の頂点を成す四つの(列)ベクトル (0
0), (1
0), (1
1), (0
1) の各々に A を掛けることによって得られる。
この行列と線型写像との間の一対一対応のもとで、行列の乗法は写像の合成に対応する[28]: 上記の A と f に加えて、k × m 行列 B が別の線型写像 g: Rm → Rk を表現するものならば、合成 g ∘ f は行列の積 BA で表現される。実際、
- (g ∘ f)(x) = g(f(x)) = g(Ax) = B(Ax) = (BA)x
である。最後の等号は行列の積の結合性による。
行列の抽象代数的側面と一般化[編集]
行列の一般化の方向性はいくつか異なるものが存在する。抽象代数学では行列の成分をもっと一般の(可換とは限らない)体や環としたものを用いるし、線型代数学は線型写像の概念を機軸に行列の性質を体系化したものである。また行や列の数を無限に増やした行列というものを考えることもできる。他の拡張としてテンソルは、(行列が矩形状あるいは二次元の数の配列と見ることができるのに対して)数の配列を高次化したものと見ることもできるし、ベクトルの双対や数列として実現することもできるものである[29]。適当な制約条件を満足する行列の集まりは、行列群あるいは線型代数群などと呼ばれる群を成す。
より一般の成分を持つ行列[編集]
しばしば実または複素成分の行列に焦点を当てることもあるが、それ以外にももっと一般の種類の成分を持った行列を考えることができる。一般化の最初の段階として任意の体(すなわち四則演算が自由にできる集合、例えば R, C 以外に有理数体 Q や有限体 Fqなど)を成分として考える。例えば符号理論では有限体上の行列を利用する。どの体で考えるとしても、固有値は多項式の根として考えることができて、それは行列の係数体の拡大体の中に存在する。たとえば、実行列の場合は固有値は複素数である。ある行列の成分をより大きな体の元と解釈しなおすことはできる(例えば実行列を全ての成分が実数であるような複素行列とみることができる)から、そのような十分大きな体の中で任意の正方行列についてその固有値全てから成る集合を考えることができる。あるいは最初から、複素数体 C のような代数閉体に成分を持つような行列のみを考えるものとすることもできる。
もっと一般に、抽象代数学では環に成分を持つ行列というものが甚だ有用である[30]。環は除法演算を持たない点において体よりも一般の概念である。この場合も、行列の加法と乗法はそのまままったく同じ物を使うことができる。R 上の n-次正方行列全体の成す集合 M(n, R) は全行列環と呼ばれる環であり、左 R-加群 Rn の自己準同型環に同型である[31]。環 R が可換環、すなわちその乗法が可換律を満たすならば、全行列環 M(n, R) は(n = 1 でない限り)非可換な R 上の単位的結合多元環となる。可換環 R 上の正方行列の行列式はライプニッツの公式を用いて定義することができて、可換環 R 上の正方行列が可逆であることの必要十分条件をその行列式が R の可逆元であることと述べることができる(これは零元でない任意の元が可逆元であった体の場合の一般化になっている)[32]。超環上の行列は超行列と呼ばれる[33]。
行列の成分が必ずしもすべて同じ環に属するというわけではない(し、すべてが全く別の環に成分を持つというわけでもない)。一つの特別な、しかしよく用いられる場合として、成分自体が行列となっているような行列と見なすこともできる区分行列が挙げられる。その成分は二次元的な行列である必要はないし、また通常の環の元である必要もないが、その大きさに関しては適当な両立条件を満足するものでなければならない。
線型写像との関係[編集]
線型写像 Rn → Rm は既に述べたように m × n 行列と等価である。一般に有限次元ベクトル空間の間の線型写像 f: V → W は(V の次元を n, W の次元を m として) V の基底 v1, …, vn と W の基底 w1, …, wm を選べば
を満たす行列 A = (aij) によって記述することができる。言い換えれば、 A の第 j-列は基底ベクトル vj の像を W の基底 {wi} に関して表したものになっている。従ってこのような関係は行列 A の成分から一意的に定まる。注意すべきは線型写像を表す行列は基底の取り方に依存することである。基底の取り方を変えれば別な行列が生じるが、それはもとの行列と同値になる[34]。既に述べた具体的な概念の多くはこの方法を通して解釈しなおすことができる。例えば転置行列 A⊤ は A の定める線型写像の転置写像を、双対基底に関して記述するものである。[35]。
より一般に、m × n 行列全体の成す集合は、勝手な単位的環 R に対して自由加群 Rm および Rn の間の R-線型写像を表すのに利用することができる。n = m のとき、そのような写像の合成を定義することができて、n-次正方行列全体の成す全行列環が、Rn の自己準同型環を表現するものとして生じる。
行列群[編集]
群というのは集合と二項演算(つまり、任意の二つの対象を結合して第三の対象を作る操作)からなる数学的構造で、適当な条件を満たすものである。行列をその元とし、行列の積を群演算とするような群は、行列群または線型代数群と呼ばれる[注釈 5][36]。群の任意の元は可逆であるから、最も一般の行列群は与えられたサイズの可逆行列全体の成す群 GLn であり、一般線型群と呼ばれる。
行列の性質のうちで積と反転に関して保たれるものを用いると、さらに別の行列群を定義することもできる。例えば、与えられたサイズの行列式が 1 であるような行列の全体は、同じサイズの一般線型群に含まれる部分群となり、特殊線型群 SLn と呼ばれる[37]。また、条件
- M⊤M = I
で定まる直交行列の全体は直交群 O(n) を成す[38]。「直交」の名は、対応する Rn の線型変換が、M を掛ける操作で二つのベクトルの内積を変えない
- (Mv) · (Mw) = v · w
という意味で角を保つことに由来する[39]。 任意の有限群は何らかの行列群同型である。なんとなれば対称群の正則表現を考えればよい[40]。故に、表現論の意味で、一般の群を比較的よくわかっている行列群を用いて調べることができる。
無限次行列[編集]
行または列の数を無限にした行列と呼べるようなものも考えることができる[41]が、そのようなものを陽なかたちに書き記すことはできないので、行を添字付ける集合と列を添字付ける集合を用意して(添字集合は必ずしも自然数から成るものでなくてよい)、それらの各元に対して行列の成分が矛盾無く定義されるという方法で扱うことになる。このとき、和・差、スカラー倍、転置といった基本演算については問題なく定義されるが、行列の乗法に関してはその成分が無限和として与えられることになり、これは(適当な制約条件を抜きにしては)一般には定義されない。
R を任意の単位的環とすれば、右 R-加群としての の自己準同型環は、I × I で添字付けられ、各列の非零成分の数が有限個であるような列有限行列の環 CFMI(R) に同型である。これと対応するものとして、左 R-加群としての M の自己準同型環を考えれば、同様に各行の非零成分の数が有限な行有限行列の環 RFMI(R) が得られる。
無限次元行列を線型写像を記述するのに用いるならば、次に述べるような理由から、その各列ベクトルが有限個の例外を除いて全ての成分が 0 となるものとならなければ無用である。A が適当な基底に関して線型写像 f: V → W を表現するものとすると、それは定義により、空間の任意のベクトルを基底ベクトルの(有限)線型結合として一意に表すことによって与えられるのであるから、従って(列)ベクトル v の成分 vi で非零となるものは有限個に限られる。また、A の各列は V の各基底ベクトルの f による像を W の基底に関して表したものとなっているから、これが意味を持つのはこれらの列ベクトルの非零成分が有限個である場合に限る。しかし一方で、A の行に関しては何の制約もない。事実、v の非零成分が有限個であるならば、積 Av はその各成分が見かけ上無限和の形で与えられるとしても、実際にはそれは非零の項が有限個しかないから、間違いなく決定することができる。さらに言えば、これは A の実質的に有限個の列の線型結合を成すことになり、また各列の非零成分は有限個だから結果として得られる和も非零成分が有限個になる。(通常は、行と列が同じ集合で添字付けられるような)与えられた型の二つの行列の積は矛盾無く定義できて、もとと同じ型を持ち、線型写像の合成に対応することも確認できる。
R がノルム環ならば、行または列に関する有限性条件を緩めることができる。すなわち、有限和の代わりに、そのノルムに関する絶対収束級数を考えればよい。例えば、列和が絶対収束列となるような行列の全体は環を成す。もちろん同様に、行和が絶対収束列となるような行列の全体も環を成す。
この文脈では、収束して連続的な問題を生じ、適当な制約条件を満たすような無限次行列はヒルベルト空間上の作用素を記述するものとして利用することができる。しかし、このようなやり方は行列としての陽な観点は曖昧になりがち[注釈 6]であり、むしろその代わりに関数解析学の抽象的でより強力な手法が利用できる。
空行列[編集]
空行列は行または列(あるいはその両方)の数が 0 であるような行列をいう[注釈 7]。零ベクトル空間を含めて写像を考える場合に、空行列は役に立つ。例えば、A が 3 × 0 行列で B が 0 × 3 行列ならば、積 AB は三次元空間 V からそれ自身への空写像に対応する 3 × 3 零行列である。空行列を表す記号というのは特に定まってはいないが、多くの数式処理システムでは空行列を作成したり空行列に関する計算をしたりすることができる。0 × 0 行列の行列式は 1 と定義される。これは行列式に関するライプニッツの公式(置換に関する和として表す公式)が空積となり、それは通常 1 であることによる。またこのことは、任意の有限次元空間における恒等変換(に対応する行列)の行列式が 1 であるという事実とも整合する。
応用[編集]
行列は数学と科学における数多くの場面で応用される。そのうちのいくつかは単に行列における数字の組を簡潔に表現するために利用させる。例えば、ゲーム理論や経済学における利得行列は2人のプレイヤーの利得を符号化する。
複素数は2×2の実行列で
のように表現することで複素数と行列における和と積をそれぞれ対応させることが可能となる。例えば2×2の回転行列は絶対値が1である複素数の乗算を表す。これと同じような解釈は一般に四元数やクリフォード代数においても可能である。
運動学やロボット工学の分野では、2次元または3次元空間における物体の位置や姿勢(回転角)を表現するのに行列が用いられ、ベクトルおよびクォータニオン(四元数)とともに姿勢制御に応用されている。任意のオイラー角は回転行列の積で表現できる。また、同次座標系での座標変換を導入するために、2次元ベクトルを座標変換する際は同次座標を追加した3次元ベクトルと3×3行列の積が、3次元ベクトルを座標変換する際は同次座標を追加した4次元ベクトルと4×4行列の積が使用される。コンピュータグラフィックスでも、アフィン変換を使って2次元平面上の図形を平行移動・回転・拡大縮小・せん断変形したり、ポリゴンメッシュや自由曲面を使って仮想空間上に物体を表現する際、物体を構成する頂点集合の位置や姿勢を表したり、カメラの画角を表現したり、3次元空間上のモデルを正規化デバイス座標系や2次元のスクリーン座標系に投影したりするのに行列が使われている。
ヒル暗号のような初期の暗号技術においても行列は用いられる。しかし、行列の線型性によって、このような暗号はかなり簡単に突破されてしまう。
グラフ理論[編集]

有限グラフの隣接行列はグラフ理論における基本的な概念である。これは枝によって繋がれたグラフの頂点を表す。また、距離行列は頂点間の距離に関する情報を含む。このような概念はハイパーリンクによって繋がれたウェブサイトや道路で繋がれた都市といった場面で応用することができる。このようなことからネットワーク理論においても行列は用いられることとなる。
解析学と幾何学[編集]
微分可能関数ƒ: Rn → Rのヘッセ行列はƒの二階導関数によって
のようになる。これは関数の局所的な状態に関する情報を符号化したものである。
脚注[編集]
注釈[編集]
- ^ 下線や二重下線などを付けることもあるが、これはタイプライター原稿で用いられた太字書体を指示する書式の名残[2]
- ^ OEDによれば、数学用語としての "matrix" の最初の用例は J. J. Sylvester in London, Edinb. & Dublin Philos. Mag. 37 (1850), p. 369: "We ‥commence‥ with an oblong arrangement of terms consisting, suppose, of m lines and n columns. This will not in itself represent a determinant, but is, as it were, a Matrix out of which we may form various systems of determinants by fixing upon a number p, and selecting at will p lines and p columns, the squares corresponding to which may be termed determinants of the pth order.
- ^ これは与えられた行列の全ての成分が加法逆元を持つ限りにおいて、加法のみから定められることに注意。特にスカラー乗法が(任意のスカラーと任意の行列に対する演算として)定義されている必要はない。従って、同じサイズの任意の行列に対する減法を定めるならば、例えば係数域が加法についてアーベル群であれば十分であるが、通例として行列の係数域は何らかの可換環と仮定するから、それには環の加法群構造を用いればよい
- ^ 正方行列でない行列に対して行列式を考える理論も存在する。これは C. E. Cullis により導入された。[27]
- ^ 普通はさらに一般線型群の閉集合となることも要求する。
- ^ "Not much of matrix theory carries over to infinite-dimensional spaces, and what does is not so useful, but it sometimes helps." [42]
- ^ "Empty Matrix: A matrix is empty if either its row or column dimension is zero",[43] "A matrix having at least one dimension equal to zero is called an empty matrix", [44]
出典[編集]
- ^ a b c d e 斎藤2017、21頁。
- ^ https://raksul.com/dictionary/underline/
- ^ Shen, Crossley & Lun 1999 cited by Bretscher 2005, p. 1
- ^ Needham, Joseph; Wang Ling (1959). Science and Civilisation in China. III. Cambridge: Cambridge University Press. p. 117. ISBN 9780521058018
- ^ Cayley 1889, pp. 475–496, vol. II.
- ^ Dieudonné 1978, p. 96, Vol. 1, Ch. III.
- ^ Merriam–Webster dictionary, Merriam–Webster 2009年4月20日閲覧。
- ^ The Collected Mathematical Papers of James Joseph Sylvester: 1837–1853, Paper 37, p. 247
- ^ Knobloch 1994.
- ^ Hawkins 1975.
- ^ Kronecker 1897.
- ^ Weierstrass 1915, pp. 271–286.
- ^ Bôcher 2004.
- ^ Mehra & Rechenberg 1987.
- ^ a b c d 斎藤2017、23頁。
- ^ a b 斎藤2017、24頁。
- ^ a b 斎藤2017、25頁。
- ^ a b 斎藤2017、31頁。
- ^ 斎藤2017、89頁。
- ^ Brown 1991, Definition II.3.3.
- ^ Greub 1975, Section III.1.
- ^ Brown 1991, Theorem II.3.22.
- ^ a b 斎藤2017、34頁。
- ^ 斎藤2017、26頁。
- ^ http://www2.math.kyushu-u.ac.jp/~tnomura/EdAct/2010TKR.pdf
- ^ Stephen P. Boyd. “Crimes against Matrices” (pdf). 2013年3月2日閲覧。
- ^ 中神祥臣・柳井晴夫 著、『矩形行列の行列式』、丸善、2012年。ISBN 978-4-621-06508-2.
- ^ Greub 1975, Section III.2.
- ^ Coburn 1955, Ch. V.
- ^ Lang 2002, Chapter XIII.
- ^ Lang 2002, XVII.1, p. 643.
- ^ Lang 2002, Proposition XIII.4.16.
- ^ Reichl 2004, Section L.2.
- ^ Greub 1975, Section III.3.
- ^ Greub 1975, Section III.3.13.
- ^ Baker 2003, Def. 1.30.
- ^ Baker 2003, Theorem 1.2.
- ^ Artin 1991, Chapter 4.5.
- ^ Artin 1991, Theorem 4.5.13.
- ^ Rowen 2008, Example 19.2, p. 198.
- ^ Itõ 1987, "Matrix".
- ^ Halmos 1982, p. 23, Chapter 5.
- ^ Glossary, O-Matrix v6 User Guide.
- ^ MATLAB Data Structures
参考文献[編集]
- Arnold, V. I.; Cooke, Roger (1992), Ordinary differential equations, Berlin, New York: Springer-Verlag, ISBN 978-3-540-54813-3
- Artin, Michael (1991), Algebra, Prentice Hall, ISBN 978-0-89871-510-1
- Association for Computing Machinery (1979), Computer Graphics, Tata McGraw–Hill, ISBN 978-0-07-059376-3
- Baker, Andrew J. (2003), Matrix Groups: An Introduction to Lie Group Theory, Berlin, New York: Springer-Verlag, ISBN 978-1-85233-470-3
- Bau III, David; Trefethen, Lloyd N. (1997), Numerical linear algebra, Philadelphia: Society for Industrial and Applied Mathematics, ISBN 978-0-89871-361-9
- Bretscher, Otto (2005), Linear Algebra with Applications (3rd ed.), Prentice Hall
- Bronson, Richard (1989), Schaum's outline of theory and problems of matrix operations, New York: McGraw–Hill, ISBN 978-0-07-007978-6
- Brown, William A. (1991), Matrices and vector spaces, New York: M. Dekker, ISBN 978-0-8247-8419-5
- Coburn, Nathaniel (1955), Vector and tensor analysis, New York: Macmillan, OCLC 1029828
- Conrey, J. B. (2007), Ranks of elliptic curves and random matrix theory, Cambridge University Press, ISBN 978-0-521-69964-8
- Fudenberg, D.; Tirole, Jean (1983), Game Theory, MIT Press
- Gilbarg, David; Trudinger, Neil S. (2001), Elliptic partial differential equations of second order (2nd ed.), Berlin, New York: Springer-Verlag, ISBN 978-3-540-41160-4
- Godsil, Chris; Royle, Gordon (2004), Algebraic Graph Theory, Graduate Texts in Mathematics, 207, Berlin, New York: Springer-Verlag, ISBN 978-0-387-95220-8
- Golub, Gene H.; Van Loan, Charles F. (1996), Matrix Computations (3rd ed.), Johns Hopkins, ISBN 978-0-8018-5414-9
- Golub, Gene H.; Van Loan, Charles F. (2013), Matrix Computations (4th ed.), Johns Hopkins, ISBN 978-1-4214-0794-4
- Greub, Werner Hildbert (1975), Linear algebra, Graduate Texts in Mathematics, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90110-7
- Halmos, Paul Richard (1982), A Hilbert space problem book, Graduate Texts in Mathematics, 19 (2nd ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-90685-0, MR675952
- Horn, Roger A.; Johnson, Charles R. (2013). Matrix analysis (Second ed.). Cambridge University Press. ISBN 978-0-521-54823-6. MR2978290
- Householder, Alston S. (1975), The theory of matrices in numerical analysis, New York: Dover Publications, MR0378371
- Krzanowski, W. J. (1988), Principles of multivariate analysis, Oxford Statistical Science Series, 3, The Clarendon Press Oxford University Press, ISBN 978-0-19-852211-9, MR969370
- Itõ, Kiyosi, ed. (1987), Encyclopedic dictionary of mathematics. Vol. I--IV (2nd ed.), MIT Press, ISBN 978-0-262-09026-1, MR901762
- Lang, Serge (1969), Analysis II, Addison-Wesley
- Lang, Serge (1987a), Calculus of several variables (3rd ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-96405-8
- Lang, Serge (1987b), Linear algebra, Berlin, New York: Springer-Verlag, ISBN 978-0-387-96412-6
- Lang, Serge (2002), Algebra, Graduate Texts in Mathematics, 211 (Revised third ed.), New York: Springer-Verlag, ISBN 978-0-387-95385-4, MR1878556
- Latouche, G.; Ramaswami, V. (1999), Introduction to matrix analytic methods in stochastic modeling (1st ed.), Philadelphia: Society for Industrial and Applied Mathematics, ISBN 978-0-89871-425-8
- Manning, Christopher D.; Schütze, Hinrich (1999), Foundations of statistical natural language processing, MIT Press, ISBN 978-0-262-13360-9
- Mehata, K. M.; Srinivasan, S. K. (1978), Stochastic processes, New York: McGraw–Hill, ISBN 978-0-07-096612-3
- Mirsky, Leonid (1990), An Introduction to Linear Algebra, Courier Dover Publications, ISBN 978-0-486-66434-7
- Nocedal, Jorge; Wright, Stephen J. (2006), Numerical Optimization (2nd ed.), Berlin, New York: Springer-Verlag, p. 449, ISBN 978-0-387-30303-1
- Oualline, Steve (2003), Practical C++ programming, O'Reilly, ISBN 978-0-596-00419-4
- Press, William H.; Flannery, Brian P.; Teukolsky, Saul A.; Vetterling, William T. (1992), “LU Decomposition and Its Applications”, Numerical Recipes in FORTRAN: The Art of Scientific Computing (2nd ed.), Cambridge University Press, pp. 34–42
- Punnen, Abraham P.; Gutin, Gregory (2002), The traveling salesman problem and its variations, Boston: Kluwer Academic Publishers, ISBN 978-1-4020-0664-7
- Reichl, Linda E. (2004), The transition to chaos: conservative classical systems and quantum manifestations, Berlin, New York: Springer-Verlag, ISBN 978-0-387-98788-0
- Rowen, Louis Halle (2008), Graduate Algebra: noncommutative view, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-4153-2
- Šolin, Pavel (2005), Partial Differential Equations and the Finite Element Method, Wiley-Interscience, ISBN 978-0-471-76409-0
- Stinson, Douglas R. (2005), Cryptography, Discrete Mathematics and Its Applications, Chapman & Hall/CRC, ISBN 978-1-58488-508-5
- Stoer, Josef; Bulirsch, Roland (2002), Introduction to Numerical Analysis (3rd ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-95452-3
- Ward, J. P. (1997), Quaternions and Cayley numbers, Mathematics and its Applications, 403, Dordrecht: Kluwer Academic Publishers Group, ISBN 978-0-7923-4513-8, MR1458894
- Wolfram, Stephen (2003), The Mathematica Book (5th ed.), Champaign, Ill: Wolfram Media, ISBN 978-1-57955-022-6
- Pappur Nagappa Shivakumar、K C Sivakumar、Yang Zhang: "Infinite Matrices and Their Recent Applications", Springer, ISBN 978-3319301792 (2016年5月25日)。
- 斎藤正彦『線形代数学』(第3版)東京図書、2017年4月10日。ISBN 978-4-489-02179-4。
物理学に関するもの[編集]
- Bohm, Arno (2001), Quantum Mechanics: Foundations and Applications, Springer, ISBN 0-387-95330-2
- Burgess, Cliff; Moore, Guy (2007), The Standard Model. A Primer, Cambridge University Press, ISBN 0-521-86036-9
- Guenther, Robert D. (1990), Modern Optics, John Wiley, ISBN 0-471-60538-7
- Itzykson, Claude; Zuber, Jean-Bernard (1980), Quantum Field Theory, McGraw–Hill, ISBN 0-07-032071-3
- Riley, K. F.; Hobson, M. P.; Bence, S. J. (1997), Mathematical methods for physics and engineering, Cambridge University Press, ISBN 0-521-55506-X
- Schiff, Leonard I. (1968), Quantum Mechanics (3rd ed.), McGraw–Hill
- Weinberg, Steven (1995), The Quantum Theory of Fields. Volume I: Foundations, Cambridge University Press, ISBN 0-521-55001-7
- Wherrett, Brian S. (1987), Group Theory for Atoms, Molecules and Solids, Prentice–Hall International, ISBN 0-13-365461-3
- Zabrodin, Anton; Brezin, Édouard; Kazakov, Vladimir; Serban, Didina; Wiegmann, Paul (2006), Applications of Random Matrices in Physics (NATO Science Series II: Mathematics, Physics and Chemistry), Berlin, New York: Springer-Verlag, ISBN 978-1-4020-4530-1
歴史に関するもの[編集]
- Bôcher, Maxime (2004), Introduction to higher algebra, New York: Dover Publications, ISBN 978-0-486-49570-5, reprint of the 1907 original edition
- Cayley, Arthur (1889), The collected mathematical papers of Arthur Cayley, I (1841–1853), Cambridge University Press, pp. 123–126
- Dieudonné, Jean, ed. (1978), Abrégé d'histoire des mathématiques 1700-1900, Paris: Hermann
- Hawkins, Thomas (1975), “Cauchy and the spectral theory of matrices”, Historia Mathematica 2: 1–29, doi:10.1016/0315-0860(75)90032-4, ISSN 0315-0860, MR0469635
- Knobloch, Eberhard (1994), “From Gauss to Weierstrass: determinant theory and its historical evaluations”, The intersection of history and mathematics, Sci. Networks Hist. Stud., 15, Basel, Boston, Berlin: Birkhäuser, pp. 51–66, MR1308079
- Kronecker, Leopold (1897), Hensel, Kurt, ed., Leopold Kronecker's Werke, Teubner
- Mehra, J.; Rechenberg, Helmut (1987), The Historical Development of Quantum Theory (1st ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-96284-9
- Shen, Kangshen; Crossley, John N.; Lun, Anthony Wah-Cheung (1999), Nine Chapters of the Mathematical Art, Companion and Commentary (2nd ed.), Oxford University Press, ISBN 978-0-19-853936-0
- Weierstrass, Karl (1915), Collected works, 3
関連項目[編集]
外部リンク[編集]
- Online Matrix Multiplication using AJAX
- Online Inverse Matrix Calculator using AJAX
- Online Calculator - Operation with matrices in R (determinant, track, inverse, adjoint, transpose)
- 『行列』 - コトバンク
- 歴史
- MacTutor: Matrices and determinants
- Matrices and Linear Algebra on the Earliest Uses Pages
- Earliest Uses of Symbols for Matrices and Vectors
- オンライン本
- Kaw, Autar K., Introduction to Matrix Algebra, ISBN 978-0-615-25126-4
- The Matrix Cookbook 2008年12月10日閲覧。
- Brookes, M. (2005), The Matrix Reference Manual, London: Imperial College 2008年12月10日閲覧。
- 『行列および行列式』荒又秀夫著、東海書房、1947年刊
- オンラインの行列計算器
- SuperiorMath (Matrix Calculator)
- Matrix Calculator (DotNumerics )
- Xiao, Gang, Matrix calculator 2008年12月10日閲覧。
- Online matrix calculator 2008年12月10日閲覧。
- Online matrix calculator(ZK framework) 2009年11月26日閲覧。
- Oehlert, Gary W.; Bingham, Christopher, MacAnova, University of Minnesota, School of Statistics 2008年12月10日閲覧。, a freeware package for matrix algebra and statistics
- Online matrix calculator 2009年12月14日閲覧。
- Operation with matrices in R (determinant, track, inverse, adjoint, transpose)
- Matrix Formulas
- 関連する学会、学術雑誌等



![{\displaystyle A=\mathbf {A} ={\begin{bmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\end{bmatrix}}={\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\end{pmatrix}}=[\mathbf {a} _{ij}]_{m\times n,(1\leq i\leq m\ ,1\leq j\leq n)}=(\mathbf {a} _{ij})_{m\times n,(1\leq i\leq m\ ,1\leq j\leq n)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa540c8d0779efbb49b81ac44b0d06753431d657)









![{\displaystyle A+B:=[a_{ij}+b_{ij}]_{i=1,\ldots ,m, \atop j=1,\ldots ,n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2da08ba99f94eeab0fd428ef4c9b51c5838c256)


![{\displaystyle \lambda A:=[\lambda a_{ij}]_{i=1,\ldots ,m, \atop j=1,\ldots ,n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/54e35db75e85fcf1b64f5ad755f18e7a160ef4f0)








![{\displaystyle {\begin{aligned}\left[{\begin{array}{cc|cc}a&b&0&0\\c&d&0&0\\\hline x&y&1&0\\z&w&0&1\end{array}}\right]\cdot \left[{\begin{array}{c|c}n&0\\m&0\\\hline q&1\\p&0\end{array}}\right]&={\begin{bmatrix}A&0\\X&E_{2}\end{bmatrix}}\cdot {\begin{bmatrix}N&0\\Q&\left[{\begin{smallmatrix}1\\0\end{smallmatrix}}\right]\end{bmatrix}}\\&={\begin{bmatrix}AN+0&0+0\\XN+E_{2}Q&0+E_{2}\left[{\begin{smallmatrix}1\\0\end{smallmatrix}}\right]\end{bmatrix}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/597c2ea829d3e5bc7d11ee1458ea9f444a3ad938)


















![{\displaystyle H(f)=\left[{\frac {\partial ^{2}f}{\partial x_{i}\,\partial x_{j}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d06a1d939d9cc74bfe40b82f3712125ae999a312)