双正則写像

長方形をアニュラスの4分の1に双正則に写す指数関数。

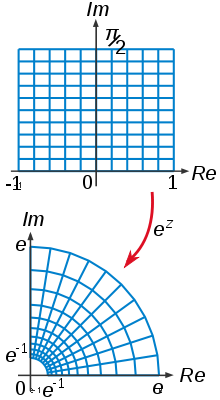
数学、特に1変数または多変数の複素解析学や複素代数幾何学において、双正則写像（そうせいそくしゃぞう、biholomorphism）とは、全単射の正則関数であって、その逆写像も正則となるもののことである。

より正確に述べると、双正則写像とは、n次元複素空間 Cⁿ の開部分集合 U で定義された全単射な Cⁿ 値正則関数 φ であって、像が Cⁿ の開集合 V であり、逆写像 φ^-1: V → U もまた正則となるもののことである。より一般には、U と V は複素多様体 (en) としてよい。φ がその像への双正則写像であるためには、単射かつ正則であれば十分であることが証明できる。

双正則写像 φ: U → V が存在するとき、U と V は双正則同値 (biholomorphically equivalent, biholomorphic) であるという。

n = 1 のときは、複素平面全体を除く単連結 (en) な開集合はすべて単位円板と双正則同値である（これをリーマンの写像定理 (en) という）。しかし、高次元では状況はまったく異なる。例えば、n > 1 のとき、単位球と単位多重円版 (en) とは双正則同値ではない。実は、正則な固有写像 (en) すら存在しない。

参考文献

• Steven G. Krantz (2002). Function Theory of Several Complex Variables. American Mathematical Society. ISBN 0-8218-2724-3. 
• John P. D'Angelo (1993). Several Complex Variables and the Geometry of Real Hypersurfaces. CRC Press. ISBN 0-8493-8272-6.