ノモグラム
ノモグラム(Nomogram)またはノモグラフ(Nomograph)または計算図表(abaque, abac)は、グラフィカルな計算のための道具であり、ある関数の計算をグラフィカルに行うために設計された二次元の図表である。1884年、フランスの技術者 Philbert Maurice d'Ocagne (1862–1938) が発明し、技術者が複雑な方程式の計算を実用的精度でグラフィカルに計算するのに使われてきた。ノモグラムは通常の直交座標系ではなく、d'Ocagne の発明した並列座標系を使うことが多い。
ノモグラムは、n 個の目盛り列で構成され、それぞれが方程式の変数に対応している。既知の n − 1 個の変数の値をノモグラムの目盛り列にプロットすると、未知の変数の値がわかるようになっている。また、既知のいくつかの変数をプロットすると未知の複数の変数の関係がわかる。目盛り上の既知の値の間を直線で結ぶと、その線と残る目盛りとの交点が未知の変数の値を示している。そのようにひいた直線を index line または isopleth とも呼ぶ。
ノモグラムは約75年間、電卓が登場する以前の素早く正確な計算手段として様々な分野でよく使われ、特に普段計算尺を使わず方程式の解法もよく知らないような人々が活用した。ノモグラムは、単に直線を1本(または数本)ひくだけで即座に計算結果を得ることができ、利用する人は対応する方程式についての知識を必要としない。例えば、精度を高めるために大きなノモグラムを作成する場合でも、利用者が興味のある妥当な範囲だけを含むよう注意を払うのが一般的である。多くの場合、ラベルを目盛りに付属させたり、領域を色づけするなどして、使いやすくする。
計算尺のようにノモグラムはグラフィカルなアナログ計算器である。計算尺と同様、その正確さは物理的にどれだけ正確にプロットし、再現し、読み取り、位置あわせできるかに依存している。多くのノモグラムはあまり正確性を求められない用途で使われている。あるいは、正確な算出方式で出てきた答えをチェックするのにノモグラムを使うこともある。計算尺は汎用の道具であることを意図している。一方ノモグラムは特定の計算を行うよう設計されていて、目盛りなどの設定を調整して効率的に計算できるようにしている。
グラフィカルな計算用の図表として他に、intercept chart、trilinear diagram、hexagonal chart などもあり、これらもノモグラムと呼ぶことがある。別の例として、電子工学やシステム解析で使われるスミスチャートがある。熱力学線図やテヒグラムは大気の垂直の構造をプロットするのに使われ、大気の安定状態や湿度を計算でき、ノモグラムの一種とされることがある。ただし、これらは1本以上の直線 (isopleth) をひくことで解が得られるグラフィカルな計算道具という定義には厳密には適合しない。
詳細[編集]

Scale: 目盛り列
Nomogram Title: 表題
Variable as Scale Title: 目盛りに対応した変数名
Label (Value): 目盛りの値
Tick Marks: 個々の目盛り
Index Line or Isopleth: 計算のためにひく直線
Scale Axis: 目盛り軸
3変数の方程式を扱うノモグラムには一般に3つの目盛り列があるが、そのうち2つまたは3つが共通の目盛り列で表されることもある。通常は、既知の2つの変数の値をプロットしてそれらを結ぶ直線をひき、第3の目盛り列とその直線の交点から未知の変数の値を読み取る。そのように求められる最も単純な方程式として u1 + u2 + u3 = 0 がある(u1, u2, u3 は変数)。各要素を解説した右図は、そのようなノモグラムの一例である。
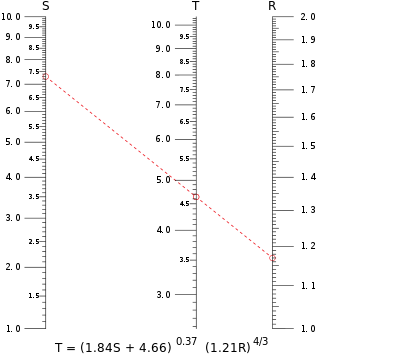
さらに複雑な方程式を3変数の総和関数として表現できる場合もある。例えば、本項目の最初に図示したノモグラムは、真数の積が対数の和に変換できるという性質を応用し、それぞれの目盛りを対数尺とすることで3変数の総和関数と同じ形式にしたものである。
未知の変数の目盛り軸は真ん中に置く場合もあるし、外側に置く場合もある。既知の変数の値をそれぞれの目盛り軸上でプロットし、それらを直線で結び、第3の目盛り軸との交点を読み取ることで、未知の変数の値がわかる。目盛り軸には数値と位置を正確に対応させるための目盛りがあり、値も書かれていることがある。目盛りは線形尺や対数尺が使われることが多いが、場合によってはもっと複雑な目盛りの配置になっている場合もある。
本項目の先頭に図示したノモグラムの例では、S = 7.30 と R = 1.17 のときの T の値を計算する様子を赤い破線で示している。Tの目盛り軸と赤い破線の交点は拡大すると 4.64 あたりと読み取れ、だいたい3桁の精度となっている。なお、3つの変数のうちどれか2つが決まれば、残る変数が求められる。代数的に解こうとすると式の変形が必要だが、ノモグラムはその必要がない。
複雑な計算を要する場合、目盛りを曲線上に並べなければならないこともある。3変数より多い変数を扱うノモグラムの場合、目盛りを格子状に配したり、3変数のノモグラムを組み合わせたりして構築できる。
用途[編集]
ノモグラムは様々な用途で使われてきた。以下に具体例を示す。
- d'Ocagne が最初のノモグラムを発明することになった計算は、フランス国鉄の線路を敷設する際の切土と盛土の複雑な計算だった。これは本項目のこれまでの図示した例のような単純な計算ではなく、ノモグラムを考案したことで大いに時間とコストを削減することに成功し、概念実証として重要な役割を果たした。
- 流水量から、水路、管、堰などを設計するための計算。
- ローレンス・ヘンダーソンは、血液生理の様々な面を関連付けるのにノモグラムを活用した。これがアメリカ合衆国での最初のノモグラム利用であり、世界初の医学への応用である。ノモグラムは医学分野でよく使われている。
- 火器管制装置が登場する以前の弾道計算(素早い計算が重要だった)。
- 機械工場で、設計図上の寸法と製造現場で実際に工作するのに必要な寸法の換算を行うのに使用した。そのようなノモグラムには標準規格部品の寸法が目盛り軸上にマークされていた。
- 統計計算用ノモグラム。分布の属性群の複雑な計算などを行う。例えば品質保証のための検査結果の検証などで使われた。
- オペレーションズ・リサーチ用ノモグラム。各種最適化問題を解く。
- 化学工学用ノモグラム。特定の化合物を生産する際の物質データや経験的データを組み合わせたもの。
- 航空用ノモグラム。航空機を操縦する際の複雑な計算をコックピットで行う場合、ノモグラムを補助的に使用していた。
- スプートニク1号の打ち上げ後の軌道計算にもノモグラムが用いられた。
- 遠心分離機のローターの半径と回転数から遠心力を求めるノモグラフ。製造メーカーのwebサイトには、自動計算するフォームも置かれている[1]。
- 年齢と血清クレアチニン値からeGFR(推定糸球体濾過量)を求めるノモグラム。
- その他、フィルタ回路や伝送線路の設計、負荷や荷重などの力学的計算、光学関連の計算など様々な工学分野で使われていた。
具体例[編集]
並列抵抗/薄レンズのノモグラム[編集]

右に示したノモグラムは次の計算を実行する。
このノモグラムは非線形の計算を直線と等間隔の目盛りだけで行うという興味深いものとなっている。
A と B は水平と垂直の目盛り軸から入力され、結果は斜めの直線上の目盛りで読み取ることができる。 A と B の調和平均を求める式だが、この式にはいくつかの用途があり、電気工学では並列抵抗の抵抗値の計算でもあるし、光学では薄レンズの焦点距離の計算でもある。
右図で、赤の線は56Ω(オーム)と42Ωの抵抗器を並列接続したときの合成抵抗が約24Ωであることを示している(オームの法則)。 また、焦点距離が24cmのレンズで56cmの距離にある物体が約42cmの距離で像を形成することも示している。
カイ二乗検定を計算するノモグラム[編集]

右に示すノモグラムは、統計学上一般的な操作であるピアソンのカイ二乗検定を近似計算するのに使われる。このノモグラムでは曲線上に非等間隔で並んだ目盛りを使用する。
対応する式は次の通りである。
最上部の目盛り軸は5種類の異なる数値の範囲に対応しており、それぞれ A、B、C、D、E とラベルが付いている。観測値 (observed) がこのうちのどれかの範囲に収まっている場合、最上部の目盛り軸にそれをプロットする。そしてAからEまでの各範囲に対応して期待値 (expected) を示す曲線がAからEまで対応している。例えば観測値が9なら、目盛り軸上の9の位置にプロットし、範囲はAということになる。したがって、Aの曲線上に期待値をプロットする。観測値が81なら、目盛り軸上の81の位置にプロットし、範囲はEということになる。そして、Eの曲線上に期待値をプロットする。これは、5種類のノモグラムを1つにまとめたものと言える。
青色の線は次の計算を示している。
- (9 − 5)2/ 5 = 3.2
赤い線は次の計算を示している。
- (81 − 70)2 / 70 = 1.7
この検定を行う際にイェイツの補正が行われ、観測値から0.5を引くことがある。イェイツの補正も同時に行うノモグラムは、単に下の図で観測値の目盛りを0.5だけずらせばよい。
関連文献[編集]
- D.P. Adams, Nomography: Theory and Application, (Archon Books) 1964.
- H.J. Allcock, J. Reginald Jones, and J.G.L. Michel, The Nomogram. The Theory and Practical Construction of Computation Charts, 5th ed., (London: Sir Isaac Pitman & Sons, Ltd.) 1963.
- S. Brodestsky, A First Course in Nomography, (London, G. Bell and Sons) 1920.
- D.S. Davis, Empirical Equations and Nomography, (New York: McGraw-Hill Book Co.) 1943.
- M. d'Ocagne: Traité de Nomographie, (Gauthier-Villars, Paris) 1899.
- M. d'Ocagne: (1900) Sur la résolution nomographique de l'équation du septième degré. Comptes rendus (Paris), 131, 522–524.
- R.D. Douglass and D.P. Adams, Elements of Nomography, (New York: McGraw-Hill) 1947.
- R.P. Hoelscher, et al., Graphic Aids in Engineering Computation, (New York: McGraw-Hill) 1952.
- L. Ivan Epstein, Nomography, (New York: Interscience Publishers) 1958.
- L.H. Johnson, Nomography and Empirical Equations, (New York: John Wiley and Sons) 1952.
- M. Kattan and J. Marasco. (2010) What Is a Real Nomogram?, Seminars in oncology, 37(1), 23–26.
- A.S. Levens, Nomography, 2nd ed., (New York: John Wiley & Sons, Inc.) 1959.
- F.T. Mavis, The Construction of Nomographic Charts, (Scranton, International Textbook) 1939.
- E. Otto, Nomography,(New York: The Macmillan Company) 1963.
- 谷村豐太郎編:「計算圖表學」、丸善(発行:初版大正9年7月25日、第8版1943年9月10日)。
- 小倉金之助 :「計算図表」、岩波全書(1946年)。
- 栗田 稔:「計算図表の原理」、 ロゴス書店(1950年)。
- 守田勝彦:「計算図表ー理論とその作り方ー」、日刊工業新聞社(1962年1月30日)。
- 花岡一昶:「電子技術者のための計算図表と作図法」、誠文堂新光社 (1969年)。
- A.S.レベンズ、藤本尚成 (訳) :「計算図表―計算図表設計技術とその応用」、ブレイン図書出版(1973年)。
脚注[編集]
関連項目[編集]
外部リンク[編集]
- ノモグラムを作ろう! 作り方および完成品PDFの公開サイト
- Weisstein, Eric W. "Nomogram". mathworld.wolfram.com (英語).
- The Art of Nomography describes the design of nomograms using geometry, determinants, and transformations.
- The Lost Art of Nomography is a math journal article surveying the field of nomography.
- Nomograms for Wargames but also of general interest.
- Java Applet for constructing simple nomograms.
- Nomograms for visualising relationships between three variables - video and slides of invited talk by Jonathan Rougier for useR!2011.


