ガイガー＝ミュラー計数管
ガイガー＝ミュラー計数管（ガイガー＝ミュラーけいすうかん、Geiger-Müller counter）は、1928年にドイツのハンス・ガイガーとヴァルター・ミュラーが開発したガイガー＝ミュラー管(Geiger-Müller tube)を応用した放射線量計測器である。
ガイガー・カウンター(Geiger counter)あるいはGM計数管とも呼ばれる。
目次 |
[編集] 概要
ガイガー=ミュラー計数管（GM管）は、主に放射線測定装置に用いられる部品。電離放射線を検知し、その回数をカウントできる[1][2]。
不活性ガスを封入した筒の中心部に電極を取付け陰陽両極に高電圧を掛けるが、通電はしていない。筒中を放射線が通過すると不活性ガスが電離され、陰極と陽極の間にパルス電流が流れるのでこの通電回数を数える。この回数が多いほどに高い線量と言うことになる。
非常に利得が高く[3]強い信号を得られる半面、一回の電離で生じた電子が次々と電離を引き起こすため放射線の持つエネルギーと出力信号の強さは比例関係にはならないので、パルス電流が流れた回数の計測 (つまり線量の測定) のみに使用され、放射線の持つエネルギー（電子ボルト）量を測定すること (つまり核種の同定) には用いられない。この装置を用いた線量計は、カウント数からベクレルもしくはシーベルトへの換算表（機種ごとに固有の係数）が添付されている。放射線のエネルギーを知るためには比例計数管などが必要である。
当該装置の発明からすでに80年近くの時間を経ているが、今日でもメジャーな線量測定装置である。ただしGM管にはその設計原理上、いくつかの固有の限界、弱点がある （徐々にカウント欠落が増える、特に高線量計測において顕著、等。一部後述）ため、実装は安価な測定器に限定され、表面線量を目安程度に計測するプライベートもしくは補助的な用途にとどまっている。
空間線量や積算線量の計測、学術・産業・業務・公的など実用的な線量計測用途にはより高価なシンチレーション検出器が使用される（これにも数種ある[4]）。これは放射線などの帯電素粒子を樹脂などに通過させ、この瞬時の現象を光学的に連続検出する装置であり、電離パルス回数を計測するGM管より計測結果が様々な使用条件において高精度である[5]。
さらに高度な分析、エネルギ・核種の同定の精密な計測には、素材にゲルマニウムなどを用いた半導体検出器が用いられるが、これは運用が非常に難しくコストもかかる。
[編集] ガイガー＝ミュラー管
ガイガー＝ミュラー管（GM管）は、1個からの電離放射線を検知することができる、GM検出器の検知部である。 これを発明したハンス・ガイガーと、ワルター・ミュラーにちなんで名づけられた。 ガイガーはアーネスト・ラザフォードと共に1908年にこの検知器を開発したが、アルファ線だけを検知できるものだった。 1928年にガイガーの教え子だったミュラーが、あらゆる種類の電離放射線を検知できるように改良した。 GM管は気体イオン検出器に分類される。
[編集] 構造と動作原理
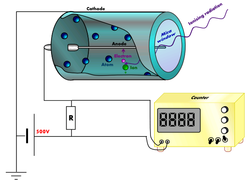
GM管はヘリウム、ネオン、またはアルゴンといった不活性ガス、もしくはペニング混合ガスを充填した中空の円筒と、その芯に取り付けられた電極から構成される。 円筒と芯の間には数百ボルトの電圧がかけられているが、通常はその間には電流は流れていない。 円筒の内壁は陰極とするため、金属またはグラファイトで作られるか、またはそれで表面をコーティングされている。 一方、円筒の中心を通る芯が陽極になっている。
電離放射線が円筒を通過すると、充填された不活性ガスの分子が電離され、正に帯電したイオンと電子を作り出す。円筒内にかけられた高電場のためにこのイオンは陰極に向かって加速され、電子は陽極に向かって加速される。これらのイオン対は加速によって運動エネルギーを得るので、移動中に衝突した気体分子もまた電離させる。こうして、ガスの中に荷電粒子のなだれが作られる。 この現象の結果、陰極から陽極に向かって短く強いパルス電流が（雪崩状に）流れ、このパルスを測定・計数することができる。
この電流が連続的に流れるとパルスの回数を計数できなくなるので、これを防ぐ（クエンチする）仕組みが存在している。 外部クエンチングは電極間の高電圧を取り除くために外部の電子機器を用いる方式である。 自己クエンチングまたは内部クエンチングは、外部の補助なしに電流を止める設計の管で、 内部に微量の多原子有機物ガス（ブタン、エタノール、または臭素や塩素のようなハロゲン）を添加してある。 イオンはクエンチガスに衝突するとそれらを解離するためにエネルギーを失うのである。
現在最も普及しているタイプは、1947年にシドニー・H・リープソンが発明したハロゲン管である。 このハロゲン管の電流発生メカニズムでは、ハロゲン分子をイオン化するのに不活性ガスの準安定状態を利用し効率的に電流を発生させるので、ずっと低い電圧でも動作できる。 通常900 - 1,200ボルトが必要なところを400 - 600ボルトで動作するのである。 また、有機ガスは再結合せず分解される一方である（およそ108回の検知が寿命）のに対し、ハロゲンイオンは再結合するので寿命も長い。
[編集] 自作
精度が低いものであれば、身近な材料で自作もできる。（YY式簡易GM管＋AMラジオ）
- ほかに、ブタン源としてライター用のガスと空気中の窒素を使用する製作方法もあるが、長持ちしないうえに危険である。
[編集] 利用と特徴
GM管は通常は端窓型管と呼ばれる形状である。これは、管の一方の端に放射線が容易に通過できるように窓があることからこう呼ばれる。反対側の端には通常は電気系のコネクターが付いている。
端窓型管にはガラスマントル型と雲母窓型の二種類が存在する。ガラス窓型は、アルファ線がガラス窓を通過できないのでアルファ線は検出できないが、大抵はより安価であることと、ベータ線とX線を検出する用途で使われる。雲母窓型はアルファ線も検出できるが、壊れやすい。
ほとんどのGM管はガンマ線と2.5MeV以上のベータ線を検出するが、ガンマ線の感度はよくない。これはGM管内のガス密度が低いため、透過力の高いガンマ線は相互作用をしにくいためである。ガンマ線を測定する目的では、NaIシンチレーション検出器の方が適しているが、逆にシンチレーション検出器は窓が厚くベータ線は透過できないので、ベータ線の検出には適していない。
中性子線はガスを電離しないので、GM管は中性子は検出できない。しかし、管の内側をホウ素でコーティングするか、三フッ化ホウ素もしくはヘリウム-3ガスを充填すれば、中性子線にも反応するGM管を作ることもできる。中性子はホウ素の原子核と反応しアルファ線を生成するか、またはヘリウム-3原子と反応して水素とトリチウムイオンと電子を生成する。そうして、これらの荷電粒子が通常のなだれを発生させる。
[編集] その他の用途
GM管は、ハードウェア乱数発生器として用いられることがある。
[編集] 日本国内での生産
1990年代まで、浜松ホトニクスが、簡易な実験的用途に適した小型軽量なGM管を製造していた。現在は製造を中止している。
[編集] 関連項目
[編集] 参考
- 日本ガイシホームページ（プラスチックコップとアルミ箔で作るガイガーカウンターの作り方）
